Overview
The single-source shortest path (SSSP) problem involves finding the shortest paths from a given source node to all other reachable nodes in a graph. In weighted graphs, the shortest path minimizes the total edge weights; in unweighted graphs, it minimizes the number of edges (hops). The cost or distance of a path refers to this total weight or count.
The concept was introduced by Dutch computer scientist Edsger W. Dijkstra in 1956, originally to determine the shortest path between two nodes. The single-source shortest path is a common variant, facilitating efficient path planning and network analysis.
Concepts
Dijkstra's Single-Source Shortest Path
Below is the basic implementation of the Dijkstra's Single-Source Shortest Path algorithm, along with an example to compute the weighted shortest paths in an undirected graph starting from the source node b:
1. Create a priority queue to store nodes and their corresponding distances from the source node. Initialize the distance of the source node as 0 and the distances of all other nodes as infinity. All nodes are marked as unvisited.

2. Extract the node with the minimum distance from the queue, mark it as visited, and relax each of its unvisited neighbors.

dist(a) = min(0+2,∞) = 2, dist(c) = min(0+1,∞) = 1
The term relaxation refers to the process of updating the distance of a node v that is connected to node u to a potential shorter distance by considering the path through node u. Specifically, the distance of node v is updated to dist(v) = dist(u) + w(u,v), where w(u,v) is the weight of the edge (u,v). This update is performed only if the current dist(v) is greater than dist(u) + w(u,v).
Once a node is marked as visited, its shortest path is fixed, and its distance will no longer change throughout the remainder of the algorithm. The algorithm only updates the distances of nodes that have not yet been visited.
3. Repeat step 2 until all nodes are visited.

dist(d) = min(1+3, ∞) = 4, dist(e) = min(1+4, ∞) = 5, dist(g) = min(1+2, ∞) = 3

dist(d) = min(2+4, 4) = 4

dist(f) = min(3+5, ∞) = 8

No neighbor can be relaxed

dist(f) = min(5+8, 8) = 8

No neighbor can be relaxed
The algorithm ends here as all nodes are visited
Considerations
- The Dijkstra's algorithm applies only to graphs with non-negative edge weights. If negative weights exist, Dijkstra's algorithm may yield incorrect results. In this case, a different algorithm like the SPFA should be used instead.
- If multiple shortest paths exist between two nodes, the algorithm will find all of them.
- In disconnected graphs, the algorithm only outputs the shortest paths from the source node to nodes within the same connected component.
Example Graph
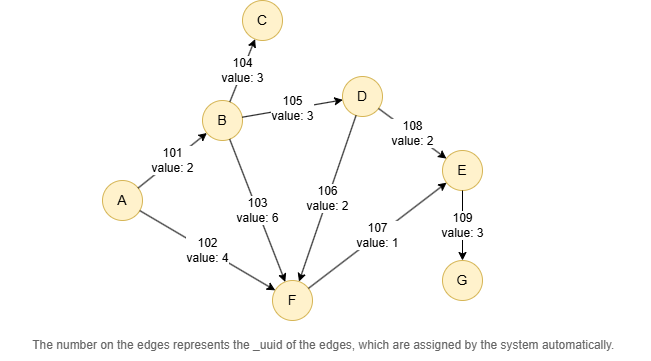
Run the following statements on an empty graph to define its structure and insert data:
ALTER EDGE default ADD PROPERTY {
value int32
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default {value: 2}]->(B),
(A)-[:default {value: 4}]->(F),
(B)-[:default {value: 3}]->(C),
(B)-[:default {value: 3}]->(D),
(B)-[:default {value: 6}]->(F),
(D)-[:default {value: 2}]->(E),
(D)-[:default {value: 2}]->(F),
(E)-[:default {value: 3}]->(G),
(F)-[:default {value: 1}]->(E);
create().edge_property(@default, "value", int32);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B", value:2}, {_from:"A", _to:"F", value:4}, {_from:"B", _to:"F", value:6}, {_from:"B", _to:"C", value:3}, {_from:"B", _to:"D", value:3}, {_from:"D", _to:"F", value:2}, {_from:"F", _to:"E", value:1}, {_from:"D", _to:"E", value:2}, {_from:"E", _to:"G", value:3}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: sssp
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
_id |
/ | / | No | Specifies a single source node by its _id. |
uuids |
_uuid |
/ | / | No | Specifies a single source node by its _uuid. |
direction |
String | in, out |
/ | Yes | Specifies that the shortest paths should only contain incoming edges (in) or outgoing edges (out); edge direction is ignored if it is unset. |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | Yes | Specifies numeric edge properties used as weights by summing their values. Only properties of numeric type are considered, and edges without these properties are ignored. |
record_path |
Integer | 0, 1 |
0 |
Yes | Whether to include the shortest paths in the results; sets to 1 to return the totalCost and the shortest paths, or to 0 to return the totalCost only. |
impl_type |
String | dijkstra |
beta |
No | Specifies the implementation type of the SSSP algorithm; for the Dijkstra's SSSP, keep it as dijkstra; beta is Ultipa's default shortest path algorithm. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. Edges can only be represented by _uuid. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
order |
String | asc, desc |
/ | Yes | Sorts the results by totalCost. |
File Writeback
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
return_id_uuid: "id"
}, {
file: {
filename: "costs"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
return_id_uuid: "id"
}).write({
file: {
filename: "costs"
}
})
Result:
_id,totalCost
D,5
F,4
B,2
E,5
C,5
G,8
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
record_path: 1,
return_id_uuid: "id"
}, {
file: {
filename: "paths"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "dijkstra",
record_path: 1,
return_id_uuid: "id"
}).write({
file: {
filename: "paths"
}
})
Result:
totalCost,_ids
8,A--[102]--F--[107]--E--[109]--G
5,A--[101]--B--[105]--D
5,A--[102]--F--[107]--E
5,A--[101]--B--[104]--C
4,A--[102]--F
2,A--[101]--B
Full Return
CALL algo.sssp.run("my_hdc_graph", {
ids: 'A',
edge_schema_property: 'value',
impl_type: 'dijkstra',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: 'value',
impl_type: 'dijkstra',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) as r
return r
} on my_hdc_graph
Result:
| _id | totalCost |
|---|---|
| G | 8 |
| D | 5 |
| E | 5 |
| C | 5 |
| F | 4 |
| B | 2 |
Stream Return
CALL algo.sssp.stream("my_hdc_graph", {
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'dijkstra',
record_path: 1,
return_id_uuid: 'id'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'dijkstra',
record_path: 1,
return_id_uuid: 'id'
}).stream() as r
return r
} on my_hdc_graph
Result:
totalCost |
_ids |
|---|---|
| 8 | ["A","102","F","107","E","109","G"] |
| 5 | ["A","101","B","105","D"] |
| 5 | ["A","102","F","107","E"] |
| 5 | ["A","101","B","104","C"] |
| 4 | ["A","102","F"] |
| 2 | ["A","101","B"] |

