What is Graph Embedding?
Graph embedding is a technique for generating latent vector representations of graphs. Graph embedding can be performed at different levels of the granularity, with the two most common being:
- Node Embeddings - Map each node in the graph to a vector.
- Graph Embeddings - Map the entire graph to a single vector.
Each vector yielded from this process is also referred to as an embedding or representation.
The term "latent" suggests that these vectors are inferred or learned from the data. They are constructed to preserve the structure (how nodes are connected) and/or attributes (node and edge properties) within the graph, which might not be explicitly visible in the original graph.
For example, in node embeddings, nodes that are more similar in the graph will have embeddings that are closer to each other in the vector space.
To illustrate, the figure below shows the results (on the right) of applying the node embedding algorithm DeepWalk to Zachary's karate club graph (on the left). In the graph, node colors indicate communities identified through modularity-based clustering. Once all the nodes have been transformed into two-dimensional vectors, it becomes evident that nodes within the same community are positioned relatively closer to each other.
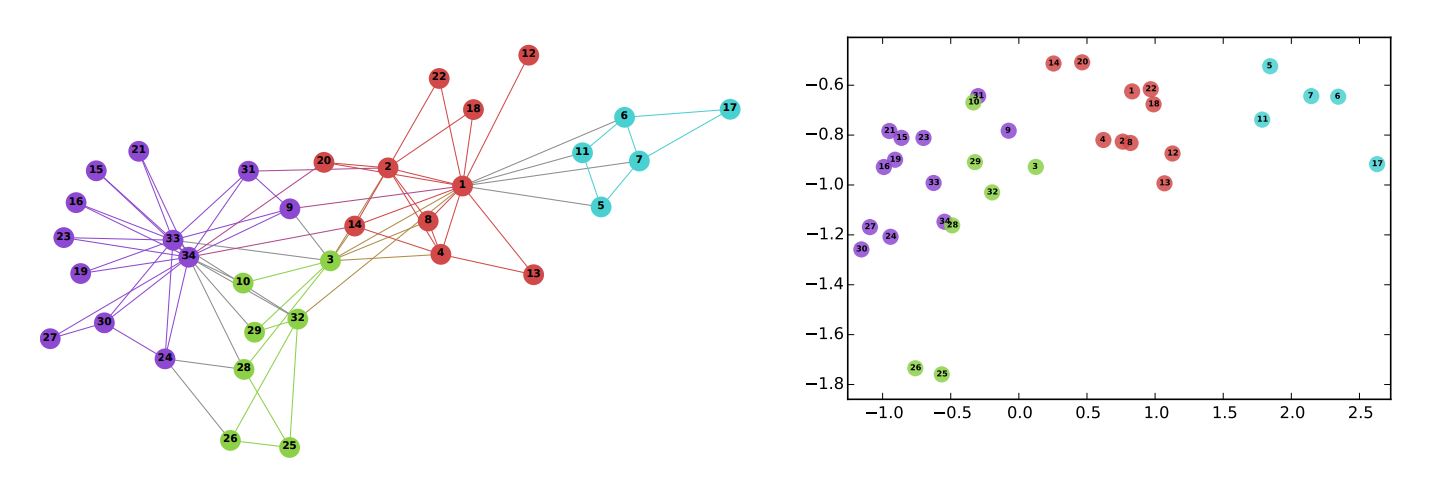B. Perozzi, et al., DeepWalk: Online Learning of Social Representations (2014)Closeness of the Embeddings
The closeness of embeddings generally refers to the spatial proximity of vectors that represent nodes or other graph elements in the embedding space. In essence, when embeddings are close together in this space, it suggests a degree of similarity in the original graph.
In practice, this closeness is measured using diverse distance or similarity metrics, such as Euclidean Distance and Cosine Similarity.
Embedding Dimension
The embedding dimension, also known as embedding size or vector size, should be chosen based on factors such as data complexity, specific tasks, and computational resources. While there is no one-size-fits-all answer, embedding dimensions in the range of 50 to 300 are commonly used in practice.
Smaller embeddings facilitate faster computation and comparisons. A practical strategy is to begin with a smaller dimension and increase it incrementally, using experimentation and performance validation to determine the most effective size for your specific application.
Why Graph Embedding?
Dimensionality Reduction
Graphs are often considered high-dimensional due to the complex relationships they encapsulate, rather than the physical dimensions they occupy.
Graph embedding serves as a dimensionality reduction method that aims to capture the most important information from graph data while substantially reducing the complexity and computational cost of working with high-dimensional data. In this context, even embeddings with a few hundred dimensions are typically regarded as low-dimensional, relative to the original representation of the graph.
Enhanced Compatibility in Data Science
Vector spaces offer dozens of advantages over graphs in terms of seamless integration with mathematical and statistical approaches in data science. Conversely, graphs, composed of nodes and edges, are limited to a narrower subset of these techniques.
A key strength of vectors is their natural compatibility with numerical computation. Each vector represents a collection of numerical features, making them inherently suitable for operations such as addition, dot products, and various transformations. These operations are not only conceptually straightforward but also computationally efficient—often resulting in significantly faster performance compared to equivalent operations on graph structures.
How Graph Embedding is Used?
Graph embedding serves as a bridge, acting as a preprocessing step for graphs. Once embeddings are generated for nodes, edges, or entire graphs, they can be used for various downstream tasks. These tasks include node classification, graph classification, link prediction, clustering and community detection, visualization, and more.
Graph Analytics
A wide range of graph algorithms exist to support diverse graph analysis tasks. While these algorithms provide valuable insights, they do have limitations. Many rely on handcrafted features derived from adjacency matrices, which may fail to capture the complex and nuanced patterns of real-world graph data. Additionally, executing these graph algorithms on large-scale graphs can be computationally intensive.
This is where graph embedding comes to play. By generating low-dimensional representations, embeddings provide richer and more flexible inputs for a wide range of analysis and tasks. These learned vectors enhance both the efficiency and accuracy of graph analysis, often outperforming algorithms that operate directly on high-dimensional graph structures.
Consider the case of node similarity analysis. Conventional similarity algorithms generally fall into two categories: neighborhood-based similarity and property-based similarity. The former, exemplified by Jaccard Similarity and Overlap Similarity, relies on the 1-hop neighborhood of nodes and computes similarity scores. The latter, represented by Euclidean Distance and Cosine Similarity, uses multiple numeric node properties to calculate the similarity scores based on property values.
While these methods have their merits, they often capture only surface-level node features, which can limit their effectiveness in complex graph scenarios. In contrast, node embeddings encode latent and higher-order structural information, enriching the input space for similarity analysis. By combining embeddings with similarity algorithms, it empowers the algorithms to consider more sophisticated relationships, leading to more meaningful analysis.
Machine Learning & Deep Learning
Contemporary machine learning (ML) and deep learning (DL) techniques have revolutionized various domains. However, applying them directly to graphs introduces unique challenges. Unlike traditional structured formats such as tabular data, graphs possess distinct characteristics, making them less compatible with standard ML/DL methods.
While there are ways to apply ML/DL to graphs, graph embedding offers a simple and effective alternative. By converting graphs or graph elements into continuous vectors, embeddings not only abstract the complexity of arbitrary graph sizes and dynamic topologies, but also enable seamless integration with modern ML/DL toolsets and libraries.
However, turning data into a compatible format for ML/DL models is not enough. Feature learning is also a significant challenge before inputting data into ML/DL models. Traditional feature engineering is both time-consuming and less accurate. In contrast, embeddings act as learned features that encapsulate both structural and attribute-based information from the graph. This enhances the model's comprehension of the data.
Imagine a social network, where nodes represent individuals and edges represent social connections. The task is to predict each individual's political affiliation. A traditional approach might involve extracting handcrafted features, such as the number of friends, average age of friends, or education levels of neighbors. These features would then be used as input to a ML model like a decision tree or random forest. However, this approach often fails to capture the complex relational patterns in the graph, treating each connection as an isolated feature and overlooking the deeper structure of the network.
In contrast, using graph embeddings allows for a richer and more integrated representation of each individual, enabling more accurate and context-aware predictions.