Overview
Shortest paths between two nodes are those with the fewest number of edges. You can select shortest paths from each partition of the match results using the following path selectors. A "partition" refers to a group of paths that share the same start and end nodes.
Path Selector |
Description |
|---|---|
ALL SHORTEST |
Selects all shortest paths from each partition. |
ANY SHORTEST |
Selects any one shortest path from each partition. |
SHORTEST k |
Selects any k (non-negative integer) shortest paths from each partition. If a partition has fewer than k shortest paths, continue selecting the second shortest, third shortest, and so on, until the required number is reached or no more paths are available. |
SHORTEST k GROUP |
Groups the paths in each partition by length, sorts the groups in ascending order, and selects all paths from the first k groups in each partition. |
The shortest path selectors are typically used with variable-length quantified paths. When a shortest path selector is used, the path mode is compulsively set to TRAIL where repeated edges are not allowed.
Note on Shortest Path Algorithms
Ultipa’s graph algorithm library includes the following shortest path algorithms:
These algorithms are recommended for computing weighted shortest paths (i.e., cheapest paths) or when calculating shortest paths over the full graph or a subgraph that has been loaded into an HDC server.
Example Graph
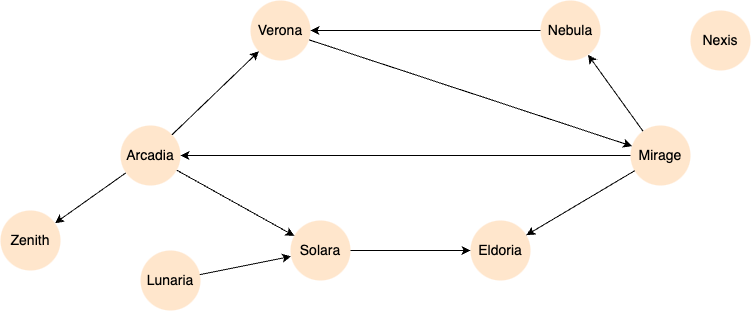
CREATE GRAPH myGraph {
NODE City ({name string}),
EDGE Links ()-[]->()
} SHARDS [1]
INSERT (zenith:City {_id: "Zenith"}),
(arcadia:City {_id: "Arcadia"}),
(verona:City {_id: "Verona"}),
(nebula:City {_id: "Nebula"}),
(mirage:City {_id: "Mirage"}),
(lunaria:City {_id: "Lunaria"}),
(solara:City {_id: "Solara"}),
(eldoria:City {_id: "Eldoria"}),
(nexis:City {_id: "Nexis"}),
(arcadia)-[:Links]->(zenith),
(arcadia)-[:Links]->(verona),
(arcadia)-[:Links]->(solara),
(mirage)-[:Links]->(arcadia),
(nebula)-[:Links]->(verona),
(mirage)-[:Links]->(nebula),
(verona)-[:Links]->(mirage),
(mirage)-[:Links]->(eldoria),
(solara)-[:Links]->(eldoria),
(lunaria)-[:Links]->(solara)
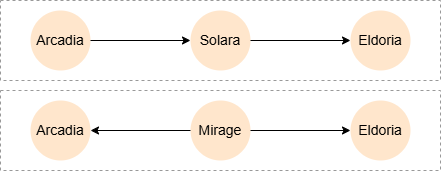
ALL SHORTEST
MATCH p = ALL SHORTEST (a)-[:Links]-+(b)
WHERE a._id = 'Arcadia' AND b._id = 'Eldoria'
RETURN p
Result: p
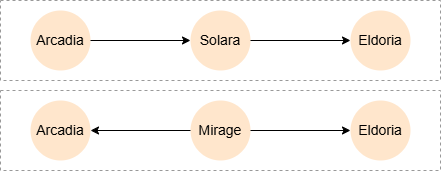
ANY SHORTEST
MATCH p = ANY SHORTEST (a)-[:Links]-{1,10}(b)
WHERE a._id = 'Arcadia' AND b._id = 'Eldoria'
RETURN p
Result: p

SHORTEST k
MATCH p = SHORTEST 2 (a)-[:Links]-{1,10}(b)
WHERE a._id = 'Arcadia' AND b._id = 'Eldoria'
RETURN p
Result: p
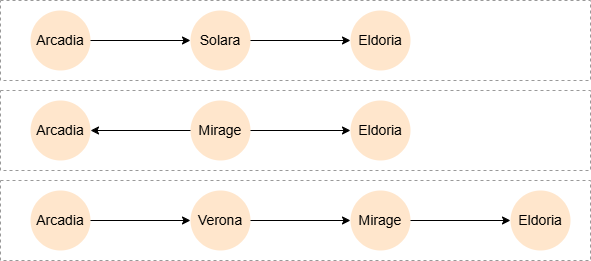
MATCH p = SHORTEST 3 (a)-[:Links]-{1,10}(b)
WHERE a._id = 'Arcadia' AND b._id = 'Eldoria'
RETURN p
Since only two paths with the shortest length of 2 exist between Arcadia and Eldoria, one path with the second shortest length needs to be selected. In this example, there is only one path with the second shortest length of 3, therefore the following three paths are returned:
SHORTEST k GROUP
MATCH p = SHORTEST 3 GROUP (a)-[:Links]-{1,10}(b)
WHERE a._id = 'Arcadia' AND b._id = 'Eldoria'
RETURN p
Two paths with the shortest length of 2, one path with the second shortest length of 3 and one path with the third shortest length of 4 are returned:

Partitions
When a path pattern matches multiple start and end nodes, the results are conceptually partitioned into distinct pairs of start node and end node. The shortest path selection is performed within each partition, and the result is the union of all shortest paths found for each partition.
In this query, the Cartesian product of a and b are generated before they are referenced in the path pattern, therefore there are four shortest paths selected from the four partitions:
MATCH p = SHORTEST 1 (a)-[:Links]-{1,10}(b)
WHERE a._id IN ['Zenith', 'Arcadia'] AND b._id IN ['Eldoria', 'Nebula']
RETURN p
Result: p
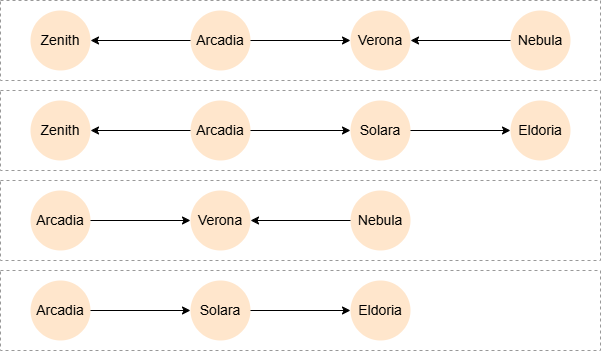
This query finds the shortest paths between Arcadia and any other city in the graph:
MATCH p = SHORTEST 1 ({_id: 'Arcadia'})-{1,10}()
RETURN p
There are 8 nodes Arcadia can reach in the graph (including itself) except Nexis. The following is one of the possible returns:


