Overview
The K-1 Coloring algorithm assigns colors to nodes so that no two adjacent nodes share the same color, while minimizing the total number of colors used.
- U.V. Çatalyürek, J. Feo, A.H. Gebremedhin, M. Halappanavar, A. Pothen, Graph Coloring Algorithms for Multi-core and Massively Multithreaded Architectures (2018)
Concepts
Distance-1 Graph Coloring
Distance-1 graph coloring, also known as K-1 graph coloring, is a concept in graph theory where the goal is to assign colors (represented by integers 0, 1, 2, ...) to the nodes of a graph such that no two nodes at distance 1 from each other (i.e., adjacent nodes) share the same color. The objective is also to minimize the number of colors used.
One of the most famous applications of graph coloring is geographical map coloring, where regions on a map are represented as nodes, and edges connect adjacent regions (those sharing a border). The task is to color the regions so that no two adjacent regions have the same color.
This concept has many practical applications beyond maps. For example, in school scheduling, each class is represented as a node, and edges indicate conflicts (such as two classes needing the same room). By coloring the graph, each class is assigned a "color" that represents a different time slot, ensuring no two conflicting classes are scheduled simultaneously.
Greedy Coloring Algorithm
The graph coloring problem is NP-hard to solved optimally, but near-optimal solutions that are near-optimal can be obtained using a greedy algorithm.
Serial Greedy Coloring Algorithm
At the beginning of the greedy algorithm, each node v in the graph is initialized as uncolored. The algorithm processes each node v as below:
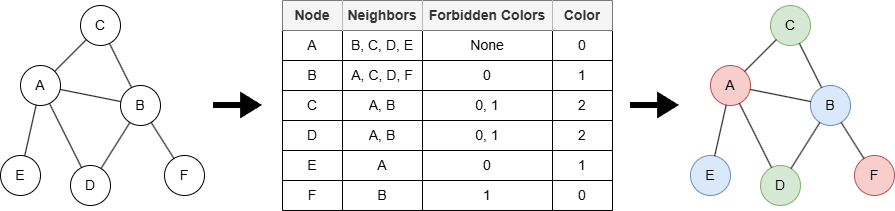
- For every adjacent node
wofv, mark the color ofwas forbidden forv. - Assign the smallest available color to
vthat is different from all its forbidden colors.
The algorithm assigns colors to nodes sequentially, which may become a bottleneck for large graphs. To address this, the following algorithm allows multiple nodes to be processed in parallel, with mechanisms to handle potential conflicts.
Iterative Parallel Greedy Coloring Algorithm
The iterative parallel greedy coloring algorithm is a parallel extension of the traditional serial greedy coloring algorithm. It is designed to leverage modern multicore and distributed computing systems, enabling more efficient processing of large graphs.
The algorithm divides the nodes in the graph into independent sets to allow concurrent processing across multiple threads. Each iteration has two phases:
- Tentative coloring phase: Similar to the serial greedy coloring algorithm, this phase assigns colors to nodes, but does so in parallel across multiple threads.
- Conflict detection phase: Each thread checks for coloring conflicts, i.e., cases where adjacent nodes (processed in different threads) have been assigned the same color. Conflicted nodes are marked for re-coloring in the next iteration.
The algorithm repeats these phases until no more nodes need to be re-colored.
Considerations
- The K-1 Coloring algorithm treats all edges as undirected, ignoring their original direction.
Example Graph
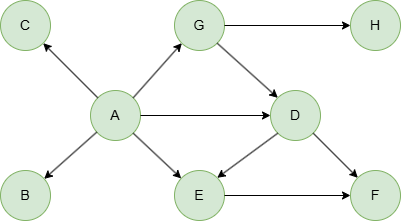
Run the following statements on an empty graph to define its structure and insert data:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(A)-[:default]->(B),
(A)-[:default]->(C),
(A)-[:default]->(D),
(A)-[:default]->(E),
(A)-[:default]->(G),
(D)-[:default]->(E),
(D)-[:default]->(F),
(E)-[:default]->(F),
(G)-[:default]->(D),
(G)-[:default]->(H);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"A", _to:"G"}, {_from:"D", _to:"E"}, {_from:"D", _to:"F"}, {_from:"E", _to:"F"}, {_from:"G", _to:"D"}, {_from:"G", _to:"H"}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: k1_coloring
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
loop_num |
Integer | ≥1 | 5 |
Yes | Number of iterations. The algorithm will terminate after completing all rounds. This option is only valid when version is set to 2. |
version |
Integer | 1, 2 |
2 |
Yes | Set to 1 to run the serial greedy coloring algorithm, or 2 to run the iterative parallel greedy coloring algorithm. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
In the results of this algorithm, nodes with the same color are considered to belong to the same community.
File Writeback
This algorithm can generate three files:
Spec |
Content |
|---|---|
filename_community_id |
|
filename_ids |
|
filename_num |
|
CALL algo.k1_coloring.write("my_hdc_graph", {
return_id_uuid: "id",
version: 1
}, {
file: {
filename_community_id: "f1.txt",
filename_ids: "f2.txt",
filename_num: "f3.txt"
}
})
algo(k1_coloring).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
version: 1
}).write({
file: {
filename_community_id: "f1.txt",
filename_ids: "f2.txt",
filename_num: "f3.txt"
}
})
Result:
_id,community_id
D,1
F,2
H,1
B,1
A,2
E,0
C,0
G,0
community_id,_ids
0,E;C;G;
2,F;A;
1,D;H;B;
community_id,count
0,3
2,2
1,3
DB Writeback
Writes the community_id values from the results to the specified node property. The property type is uint32.
CALL algo.k1_coloring.write("my_hdc_graph", {
loop_num: 10,
version: 2
}, {
db: {
property: "color"
}
})
algo(k1_coloring).params({
projection: "my_hdc_graph",
loop_num: 10,
version: 2
}).write({
db: {
property: "color"
}
})
Stats Writeback
CALL algo.k1_coloring.write("my_hdc_graph", {
version: 1
}, {
stats: {}
})
algo(k1_coloring).params({
projection: "hdc_coloring",
version:1
}).write({
stats: {}
})
Result:
| community_count |
|---|
| 3 |
Full Return
CALL algo.k1_coloring.run("my_hdc_graph", {
return_id_uuid: "id",
loop_num: 5,
version: 2
}) YIELD r
RETURN r
exec{
algo(k1_coloring).params({
return_id_uuid: "id",
loop_num: 5,
version: 2
}) as r
return r
} on my_hdc_graph
Result:
| _id | community_id |
|---|---|
| D | 1 |
| F | 2 |
| H | 1 |
| B | 1 |
| A | 2 |
| E | 0 |
| C | 0 |
| G | 0 |
Stream Return
CALL algo.k1_coloring.stream("my_hdc_graph", {
return_id_uuid: "id",
loop_num: 15,
version: 1
}) YIELD r
RETURN r.community_id AS communityID, count(r) AS nodeCounts GROUP BY communityID
exec{
algo(k1_coloring).params({
return_id_uuid: "id",
loop_num: 15,
version: 1
}).stream() as r
group by r.community_id as communityID
with r, count(r) as nodeCounts
return table(communityID, nodeCounts)
} on my_hdc_graph
Result:
| communityID | nodeCounts |
|---|---|
| 0 | 3 |
| 1 | 3 |
| 2 | 2 |
Stats Return
CALL algo.k1_coloring.stats("my_hdc_graph") YIELD res
RETURN res
exec{
algo(k1_coloring).params().stats() as res
return res
} on my_hdc_graph
Result:
| community_count |
|---|
| 3 |

