Overview
The basic Skip-gram model is nearly impractical for real-world use due to its high computational demands.
The sizes of the matrices and depend on the vocabulary size (e.g., ) and the embedding dimension (e.g., ). As a result, each matrix can contain millions of weights (e.g., million), making the Skip-gram neural network substantially large. Training such a model effectively requires a massive number of samples to tune all the weights.
Additionaly, during each backpropagation step, updates are applied to all output vectors () in matrix , even though most of these vectors are unrelated to the current target or context words. Given the large size of , this makes gradient descent highly inefficient and computationally slow.
Another significant computational cost comes from the Softmax function, which involves all words in the vocabulary to compute the normalization denominator.
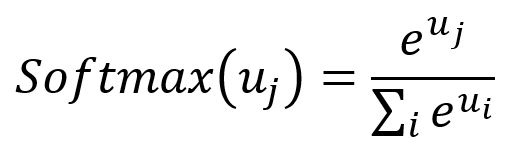
T. Mikoliv and colleagues introduced optimization techniques for the Skip-gram model, including subsampling and negative sampling. These approaches help accelerate training and improve the quality of the resulting embedding vectors.
- T. Mikolov, I. Sutskever, K. Chen, G. Corrado, J. Dean, Distributed Representations of Words and Phrases and their Compositionality (2013)
- X. Rong, word2vec Parameter Learning Explained (2016)
Subsampling
Common words in the corpus, such as "the", "and", and "is", raise certain concerns:
- They have limited semantic value. For example, the model benefits more from the co-occurrence of "France" and "Paris" than from the frequent pairing of "France" and "the".
- These words show up in more training samples than needed, making it inefficient to train their vectors.
Subsampling is used to address this issue by randomly discarding words during training. Frequent words are more likely to be discarded, while rare words are kept more often.
First, calculate the probability of keeping a word by:
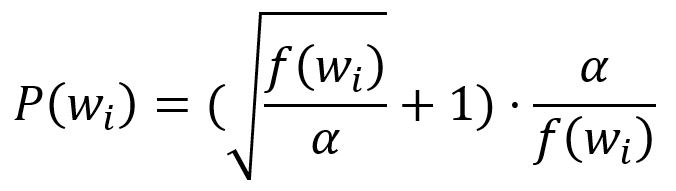
where is the frequency of the -th word, is a factor that influences the distribution and is default to .
Then, a random number between and is generated. If is smaller than this number, the word is discarded.
For instance, when , then for , , so words with frequency or less will 100% be kept. For a high word frequency like , .
In the case when , then words with frequency or less will 100% be kept. For the same high word frequency , .
Thus, a higher value of increases the probability that frequent nodes are down-sampled.
For example, if the word 'a' is discarded from the sentence 'Graph is a good way to visualize data,' then no training samples will include 'a' as either the target or a context word.
Negative Sampling
In the negative sampling approach, when a positive context word is sampled for a target word, a total of words are simultaneously chosen as negative samples.
For instance, let's consider the simple corpus when discussing the basic Skip-gram model. This corpus comprises a vocabulary of 10 words: graph, is, a, good, way, to, visualize, data, very, at. When the positive sample (target, content): (is, a) is generated using a sliding window, we select negative words graph, data and at to accompany it:
| Target Word | Context Word | Expected Output | |
|---|---|---|---|
| is | Positive Sample | a | 1 |
| Negative Samples | graph | 0 | |
| data | 0 | ||
| at | 0 |
With negative sampling, the training objective of the model shifts from predicting context words for the target word to a binary classification task. In this setup, the output for the positive word is expected as , while the outputs for the negative words are expected as ; other words that do not fall into either category are disregarded.
Consequently, during the backpropagation process, the model only updates the output vectors associated with the positive and negative words to improve the model's classification performance.
Consider the scenario where and . When applying negative sampling with the parameter , only individual weights in will require updates, which is of the million weights to be updated without negative sampling!
Our experiments indicate that values of in the range are useful for small training datasets, while for large datasets the can be as small as . (Mikolov et al.)
To select negative samples, a probability distribution is required. The fundamental principle is to prioritize frequent words in the corpus. However, using raw frequency can result in an overrepresentation of very common words, while underrepresenting less frequent ones. To address this, an empirical distribution is often used that involves raising the word frequency to the power of :
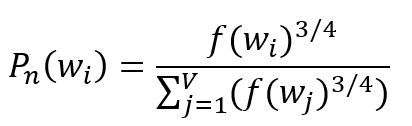
where is the frequency of the -th word, the subscript of indicates the concept of noise, the distribution is also called the noise distribution.
In extreme cases, consider a corpus containing only two words, with frequencies of and respectively. Applying the above formula results in adjusted probabilities of and . This adjustment helps reduce the bias caused by large frequency disparities.
However, when working with large corpora, negative sampling can still be computationally intensive. To address this, a resolution is introduced to rescale the noise distribution. A higher resolution value enables the resampled distribution to better approximate the original noise distribution, striking a balance between efficiency and accuracy.
Optimized Model Training
Forward Propagation
We will demonstrate with target word is, positive word a, and negative words graph, data and at:

With negative sampling, the Skip-gram model uses the following variation of the Softmax function, which is actually the Sigmoid function () of . This function maps all components of within the range of and :
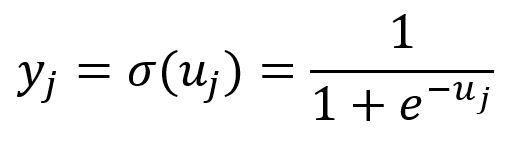
Backpropagation
As explained, the output for the positive word, denoted as , is expected to be ; while the outputs corresponding to the negative words, denoted as , are expected to be . Therefore, the objective of the model's training is to maximize both and , which can be equivalently interpreted as maximizing their product:
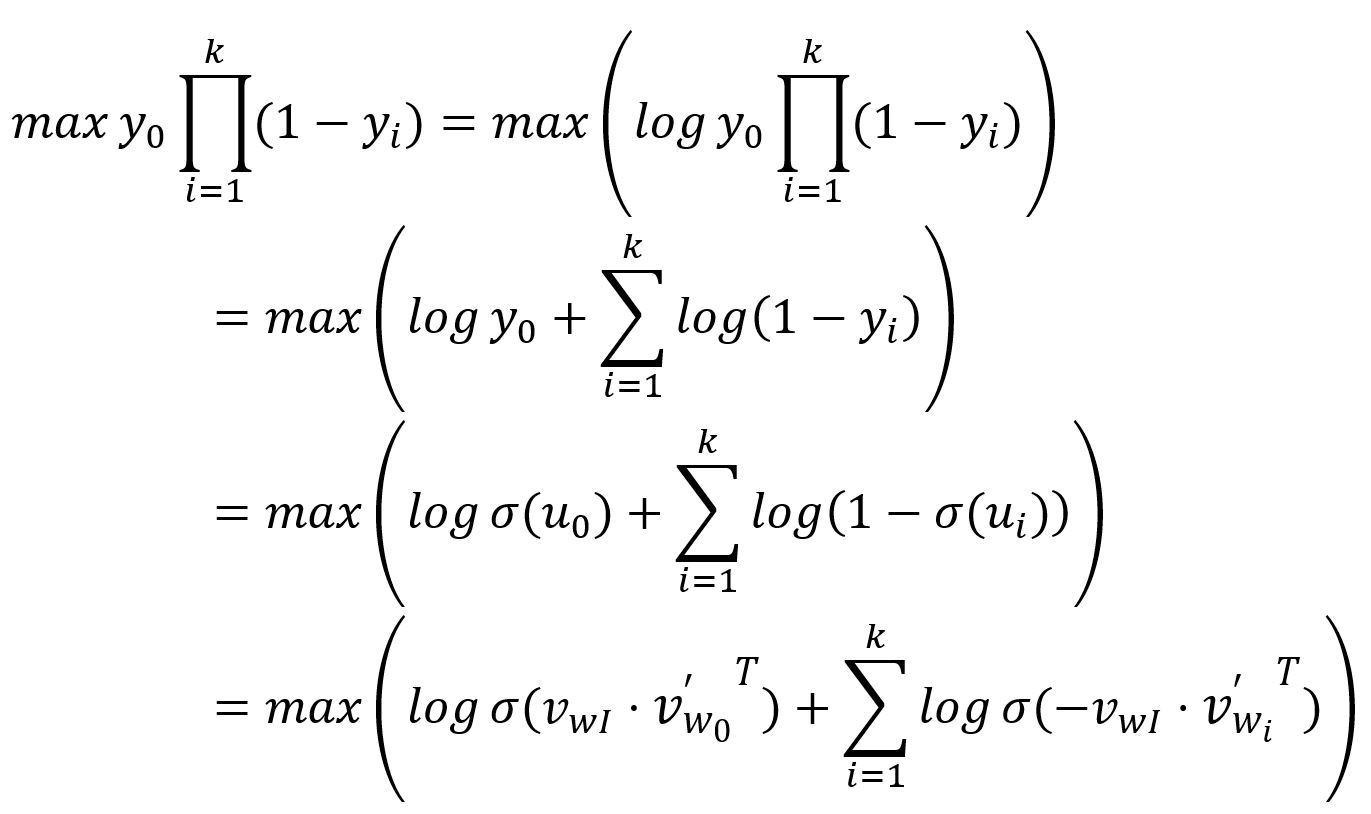
The loss funtion is then obtained by transforming the above as a minimization problem:
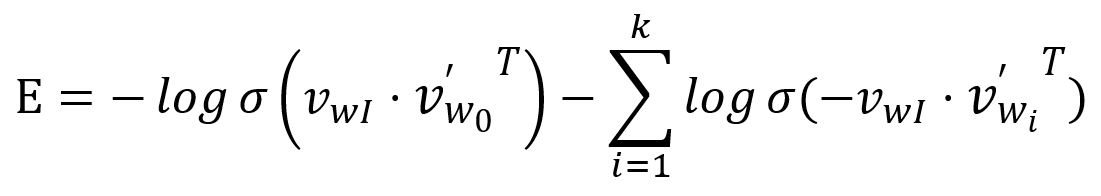
Take the partial derivative of with respect to and :
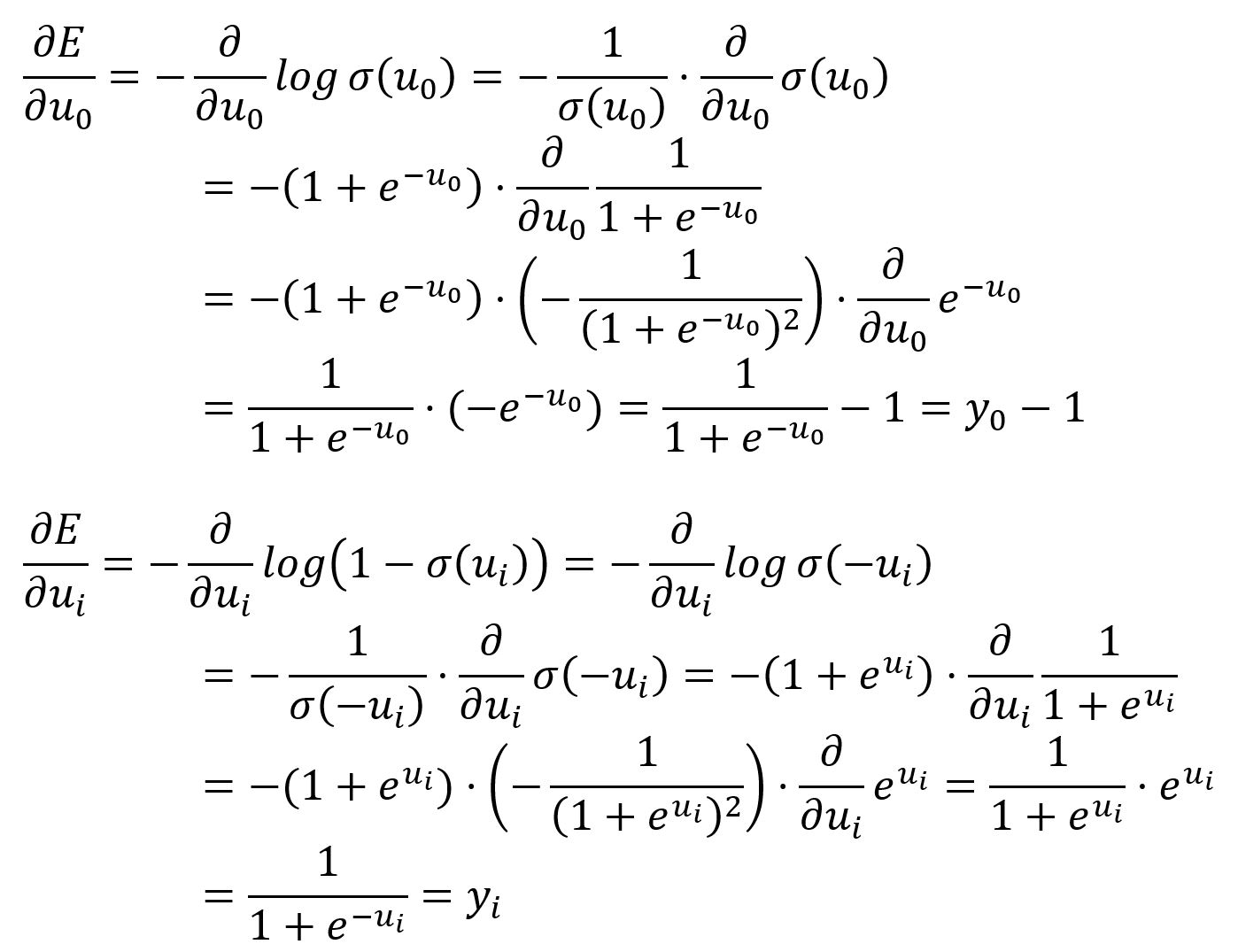
and hold a similar meaning to in the original Skip-gram model, which can be understood as subtracting the expected vector from the output vector:
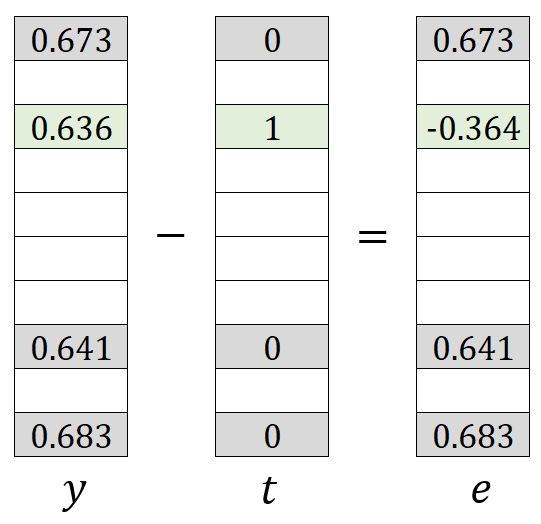
The process of updating weights in matrices and is straightforward. You may refer to the original form of Skip-gram. However, only weights , , , , , , and in and weights and in are updated.

