Struc2Vec

Overview

Struc2Vec, short for "structure to vector", is an algorithm that generates node embeddings while preserving the graph's structural properties. It focuses on capturing topological similarities between nodes, enabling structurally similar nodes to have similar vector representations.

• L. Ribeiro, P. Saverese, D. Figueiredo, struc2vec: Learning Node Representations from Structural Identity (2017)

While Node2Vec captures a certain degree of structural similarity among nodes, it is limited by the depth of random walks used during the generation process.Struc2Vec, on the other hand, overcomes this limitation by explicitly preserving structural roles, ensuring that nodes with similar topological characteristics are positioned closely in the embedding space.

The choice between Node2Vec and Struc2Vec depends on the nature of downstream tasks:

• Node2Vec is better suited for tasks that emphasize node homophily, capturing similarity in attributes and connections.
• Struc2Vec is ideal for tasks that focus on local topology similarity, preserving the structural relationships among nodes.

Concepts

Structural Similarity

In various networks, nodes often exhibit distinct structural identities that reflect their specific functions or roles. Nodes that perform similar functions naturally belong to the same class, signifying a high degree of structural similarity. For instance, in a company's social network, all interns might exhibit similar structural roles.

Structural similarity implies that the neighborhood topologies of such nodes are homogenous or symmetrical. In other words, nodes with similar functions tend to have analogous patterns of connections and relationships with their neighbors.

As illustrated here, nodes u and v are structurally similar—they have degrees of 5 and 4, are connected to 3 and 2 triangles respectively, and each connects to the rest of the network through 2 nodes. Despite not sharing a direct link or common neighbor, and possibly being far apart in the graph, they still exhibit similar structural roles.

However, when the distance between such nodes exceeds the walk depth, methods like Node2Vec struggle to generate similar representations for them. This limitation is effectively addressed by the Struc2Vec algorithm.

Struc2Vec Framework

1. Measure structural similarity

Intuitively, two nodes with the same degrees are considered structurally similar. If their neighbors also share the same degrees, the structural similarity between the two nodes becomes even stronger.

Consider an undirected, unweighted graph G = (V, E), with diameter denoted as k*. Let R_k(u) represent the set of nodes that are exactly k hops away from node u, where k ∈ [0, k*]. Let s(S) denote the ordered degree sequence of a node set S ⊂ V. Here is an example:

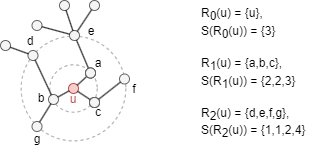
Let f_k(u,v) denote the structural distance between nodes u and v, considering their k-hop neighborhoods (all nodes within a distance less than or equal to k):

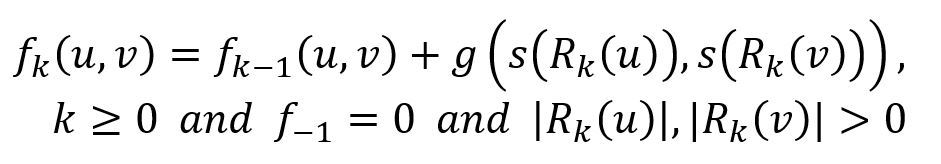
where function g() ≥ 0 measures the distance between two degree sequences. Note that f_k(u,v) is non-decreasing in k and is defined only when both u and v have neighbors at distance k.

To measure the distance between the sequences s(R_k(u)) and s(R_k(v)), which may differ in length, Dynamic Time Wrapping (DTW), or any other appliable function, can be adopted. Note that if the k-hop neighborhoods of nodes u and v are isomorphic, then f_k-1(u,v) = 0.

2. Construct a multilayer weighted graph

Struc2Vec constructs a multilayer weighted graph M that encodes structural similarity between nodes, where each layer k is defined using the k-hop neighborhoods of the nodes.

Each layer k forms a weighted, undirected complete graph with node set V, containing $\frac{\mathrm{|V|*(|V|-1)}}{2}$ edges. The edge weight between nodes u and v is inversely proportional to their structural distance, as defined as:

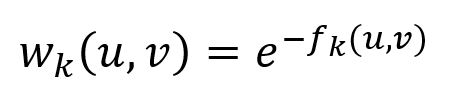
Note that edges are defined only if f_k(u,v) is defined.

Layers are connected by directed edges. Every node is connected to its corresponding node in the adjacent layers (if such layers exist). The weights of these inter-layer edges are as follows:

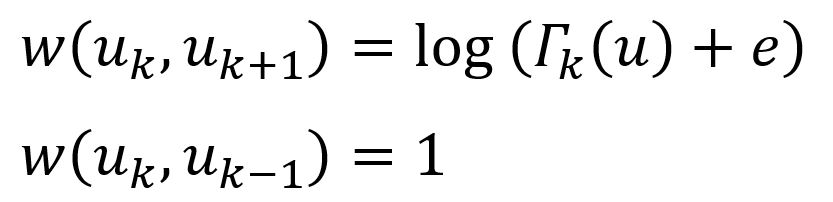
where Γ_k(u) is the number of edges incident to u that have weight larger than the average edge weight of the complete graph in layer k. Γ_k(u) actually measures the similarity of node u to other nodes in layer k. Note that if node u has many similar nodes in layer k, then it should change to higher layers to obtain a more refined context.

3. Generate context for nodes

Struc2Vec uses random walks to generate sequence of nodes to determine the context of a gievn node.

Consider a biased random walk that operates on graph M. Each node starts the walk in its corresponding node in layer 0. When the walk reaches node u in layer k (denoted as u_k), the random walk first decides if it will (1) stay in the current layer, or (2) change layer:

(1) With probability q, the random walk stays in the current layer: the probability of moving to v_k is proportional to w_k(u,v). Note that the random walk will prefer to step onto nodes that are structurally more similar to the current node.

(2) With probability 1 − q, the random walk changes layer: the probabilities of moving to u_k+1 or u_k-1 are proportional to w_k(u_k,u_k+1) and w_k(u_k,u_k-1). It's important to note that in this case, the node u is recorded only once in the random walk sequence.

The random walks have a fixed and relatively short depth (number of steps), and the process is repeated a certain number of times.

4. Train the model

The node sequences generated from the random walks serve as input to the Skip-gram model. SGD is used to optimize the model's parameters based on the prediction error, with optimization techniques such as negative sampling and subsampling applied to enhance efficiency.

Considerations

• When calculating the degree of a node, each self-loop is counted twice.
• The Struc2Vec algorithm treats all edges as undirected, ignoring their original direction.

Example Graph

Run the following statements on an empty graph to define its structure and insert data:

INSERT (A:default {_id: "A"}),
       (B:default {_id: "B"}),
       (C:default {_id: "C"}),
       (D:default {_id: "D"}),
       (E:default {_id: "E"}),
       (F:default {_id: "F"}),
       (G:default {_id: "G"}),
       (H:default {_id: "H"}),
       (I:default {_id: "I"}),
       (J:default {_id: "J"}),
       (A)-[:default]->(B),
       (A)-[:default]->(C),
       (D)-[:default]->(C),
       (D)-[:default]->(F),
       (E)-[:default]->(C),
       (E)-[:default]->(F),
       (F)-[:default]->(G),
       (G)-[:default]->(J),
       (H)-[:default]->(G),
       (H)-[:default]->(I);

insert().into(@default).nodes([{_id:"A"},{_id:"B"},{_id:"C"},{_id:"D"},{_id:"E"},{_id:"F"},{_id:"G"},{_id:"H"},{_id:"I"},{_id:"J"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"D", _to:"C"}, {_from:"D", _to:"F"}, {_from:"E", _to:"C"}, {_from:"E", _to:"F"}, {_from:"F", _to:"G"}, {_from:"G", _to:"J"}, {_from:"H", _to:"G"}, {_from:"H", _to:"I"}]);

Creating HDC Graph

To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:

CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static"
}

hdc.graph.create("my_hdc_graph", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static"
}).to("hdc-server-1")

Parameters

Algorithm name: struc2vec

File Writeback

CALL algo.struc2vec.write("my_hdc_graph", {
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 5,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}, {
  file: {
    filename: "embeddings"
  }
})

algo(struc2vec).params({
  projection: "my_hdc_graph",
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 5,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}).write({
  file: {
    filename: "embeddings"
  }
})

DB Writeback

Writes the embedding_result values from the results to the specified node property. The property type is float[].

CALL algo.struc2vec.write("my_hdc_graph", {
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 4,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}, {
  db: {
    property: "vector"
  }
})

algo(struc2vec).params({
  projection: "my_hdc_graph",
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 4,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}).write({
  db: {
      property: "vector"
    }
})

Full Return

CALL algo.struc2vec.run("my_hdc_graph", {
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 4,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}) YIELD embeddings
RETURN embeddings

exec{
  algo(struc2vec).params({
    return_id_uuid: "id",
    walk_length: 10,
    walk_num: 20,
    k: 10,
    stay_probability: 0.4,
    window_size: 5,
    dimension: 4,
    loop_number: 10,
    learning_rate: 0.01,
    min_learning_rate: 0.0001,
    neg_number: 9,
    resolution: 100,
    sub_sample_alpha: 0.001,
    min_frequency: 3
  }) as embeddings
  return embeddings
} on my_hdc_graph

Stream Return

CALL algo.struc2vec.stream("my_hdc_graph", {
  return_id_uuid: "id",
  walk_length: 10,
  walk_num: 20,
  k: 10,
  stay_probability: 0.4,
  window_size: 5,
  dimension: 5,
  loop_number: 10,
  learning_rate: 0.01,
  min_learning_rate: 0.0001,
  neg_number: 9,
  resolution: 100,
  sub_sample_alpha: 0.001,
  min_frequency: 3
}) YIELD embeddings
RETURN embeddings

exec{
  algo(struc2vec).params({
    return_id_uuid: "id",
    walk_length: 10,
    walk_num: 20,
    k: 10,
    stay_probability: 0.4,
    window_size: 5,
    dimension: 5,
    loop_number: 10,
    learning_rate: 0.01,
    min_learning_rate: 0.0001,
    neg_number: 9,
    resolution: 100,
    sub_sample_alpha: 0.001,
    min_frequency: 3
  }) as embeddings
  return embeddings
} on my_hdc_graph