Overview
The Shortest Path Faster Algorithm (SPFA) is an improvement of the Bellman–Ford algorithm which computes the shortest paths from a source node to all other reachable nodes (i.e., single-source shortest paths) in a graph. It is especially well-suited for graphs with negative-weight edges.
The algorithm was first published by E.F. Moore in 1959, but it was later rediscovered and popularized under the name "Shortest Path Faster Algorithm (SPFA)" by FanDing Duan in 1994.
- F. Duan, 关于最短路径的SPFA快速算法 [About the SPFA algorithm] (1994)
Concepts
Shortest Path Faster Algorithm (SPFA)
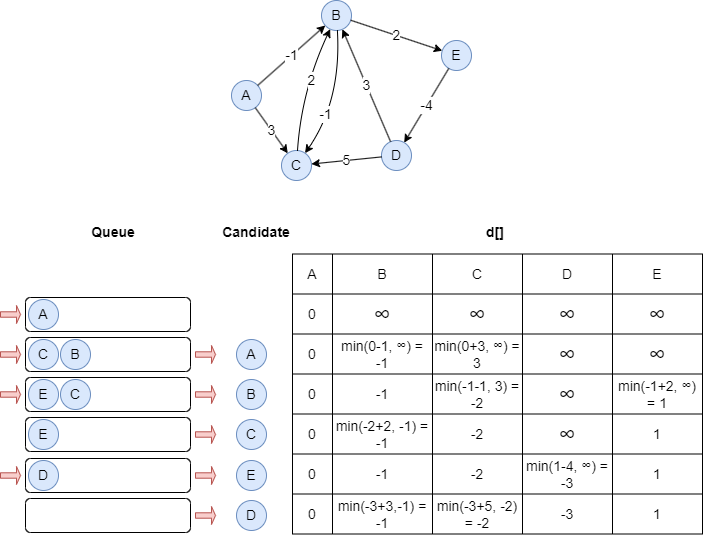
Given a graph G = (V, E) and a source node s∈V, array d[] is used to store the distances of the shortest paths from s to all nodes. Initialize all elements in d[] to infinity, except for d[s] = 0.
The basic idea of SPFA is the same as the Bellman–Ford algorithm in that each node is used as a candidate to relax its adjacent nodes. However, SPFA improves efficiency by avoiding unnecessary iterations over all nodes. Instead, it maintains a first-in, first-out queue Q to store candidate nodes, and a node is added to the queue only when it has been relaxed.
The term relaxation refers to the process of updating the distance of a node v that is connected to node u to a potential shorter distance by considering the path through node u. Specifically, the distance of node v is updated to d[v] = d[u] + w(u,v), where w(u,v) is the weight of the edge (u,v). This update is performed only if the current d[v] is greater than d[u] + w(u,v).
At the begining of the algorithm, all nodes are assigned an initial distance of infinity, except for the source node, which is set to 0. The source node is viewed as first relaxed and pushed into the queue.
During each iteration, SPFA dequeues a node u from Q as a candidate. For each edge (u,v) in the graph, if node v can be relaxed, the following steps are performed:
- Relax node v: d[v] = d[v] + w(u,v).
- Push node v into Q if v is not in Q.
This process repeats until no more nodes can be relaxed.
The steps below illustrate how to compute the SPFA with source node A and find the weighted shortest paths in the outgoing direction:
Considerations
- SPFA can handle graphs with negative edge weights under the conditions that (1) the source node does not have access to any node within a negative cycle, and (2) the shortest paths are directed. A negative cycle is a cycle where the sum of the edge weights is negative. If the graph contains such cycles or if shortest paths are undirected when negative weights exist, SPFA will output infinite results. This occurs because the algorithm can repeatedly traverse the negative cycle or edge, continually lowering the path cost each time.
- If multiple shortest paths exist between two nodes, the algorithm will find all of them.
- In disconnected graphs, the algorithm only outputs the shortest paths from the source node to all nodes belonging to the same connected component as the source node.
Example Graph
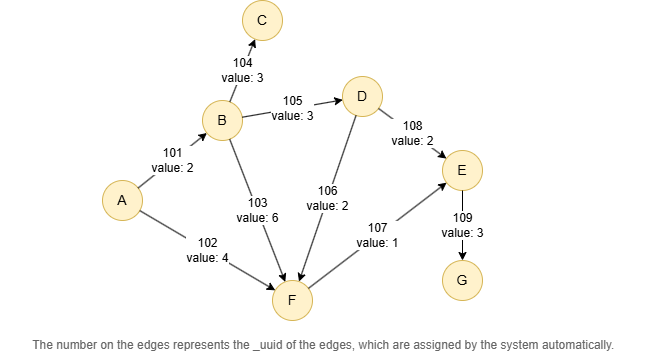
Run the following statements on an empty graph to define its structure and insert data:
ALTER EDGE default ADD PROPERTY {
value int32
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default {value: 2}]->(B),
(A)-[:default {value: 4}]->(F),
(B)-[:default {value: 3}]->(C),
(B)-[:default {value: 3}]->(D),
(B)-[:default {value: 6}]->(F),
(D)-[:default {value: 2}]->(E),
(D)-[:default {value: 2}]->(F),
(E)-[:default {value: 3}]->(G),
(F)-[:default {value: 1}]->(E);
create().edge_property(@default, "value", int32);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B", value:2}, {_from:"A", _to:"F", value:4}, {_from:"B", _to:"F", value:6}, {_from:"B", _to:"C", value:3}, {_from:"B", _to:"D", value:3}, {_from:"D", _to:"F", value:2}, {_from:"F", _to:"E", value:1}, {_from:"D", _to:"E", value:2}, {_from:"E", _to:"G", value:3}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: sssp
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
_id |
/ | / | No | Specifies a single source node by its _id. |
uuids |
_uuid |
/ | / | No | Specifies a single source node by its _uuid. |
direction |
String | in, out |
/ | Yes | Specifies that the shortest paths should only contain incoming edges (in) or outgoing edges (out); edge direction is ignored if it is unset. |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | Yes | Specifies numeric edge properties used as weights by summing their values. Only properties of numeric type are considered, and edges without these properties are ignored. |
record_path |
Integer | 0, 1 |
0 |
Yes | Whether to include the shortest paths in the results; sets to 1 to return the totalCost and the shortest paths, or to 0 to return the totalCost only. |
impl_type |
String | spfa |
beta |
No | Specifies the implementation type of the SSSP algorithm; for the SPFA, keep it as spfa; beta is Ultipa's default shortest path algorithm. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. Edges can only be represented by _uuid. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
order |
String | asc, desc |
/ | Yes | Sorts the results by totalCost. |
File Writeback
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "spfa",
return_id_uuid: "id"
}, {
file: {
filename: "costs"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "spfa",
return_id_uuid: "id"
}).write({
file: {
filename: "costs"
}
})
Result:
_id,totalCost
D,5
F,4
B,2
E,5
C,5
G,8
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "spfa",
record_path: 1,
return_id_uuid: "id"
}, {
file: {
filename: "paths"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "spfa",
record_path: 1,
return_id_uuid: "id"
}).write({
file: {
filename: "paths"
}
})
Result:
totalCost,_ids
8,A--[102]--F--[107]--E--[109]--G
5,A--[101]--B--[105]--D
5,A--[102]--F--[107]--E
5,A--[101]--B--[104]--C
4,A--[102]--F
2,A--[101]--B
Full Return
CALL algo.sssp.run("my_hdc_graph", {
ids: 'A',
edge_schema_property: 'value',
impl_type: 'spfa',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: 'value',
impl_type: 'spfa',
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) as r
return r
} on my_hdc_graph
Result:
| _id | totalCost |
|---|---|
| G | 8 |
| D | 5 |
| E | 5 |
| C | 5 |
| F | 4 |
| B | 2 |
Stream Return
CALL algo.sssp.stream("my_hdc_graph", {
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'spfa',
record_path: 1,
return_id_uuid: 'id'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'spfa',
record_path: 1,
return_id_uuid: 'id'
}).stream() as r
return r
} on my_hdc_graph
Result:
totalCost |
_ids |
|---|---|
| 8 | ["A","102","F","107","E","109","G"] |
| 5 | ["A","101","B","105","D"] |
| 5 | ["A","102","F","107","E"] |
| 5 | ["A","101","B","104","C"] |
| 4 | ["A","102","F"] |
| 2 | ["A","101","B"] |

