Overview
The Common Neighbors algorithm measures the similarity between two nodes by counting how many neighbors they share.
The logic behind this algorithm is that two nodes with many common neighbors are more likely to be similar or have a potential connection. This similarity score is calculated using the following formula:
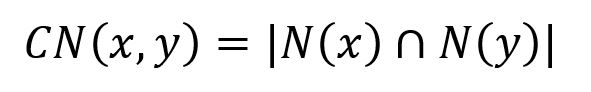
where N(x) and N(y) are the sets of adjacent nodes to nodes x and y respectively.
More common neighbors indicate greater similarity between nodes, while a number of 0 indicates no similarity between two nodes.
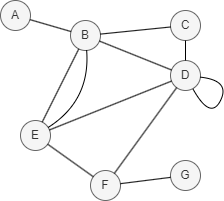
In this example, CN(D,E) = |N(D) ∩ N(E)| = |{B, F}| = 2.
Considerations
- The Common Neighbors algorithm treats all edges as undirected, ignoring their original direction.
Example Graph
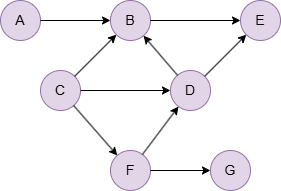
Run the following statements on an empty graph to define its structure and insert data:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default]->(B),
(B)-[:default]->(E),
(C)-[:default]->(B),
(C)-[:default]->(D),
(C)-[:default]->(F),
(D)-[:default]->(B),
(D)-[:default]->(E),
(F)-[:default]->(D),
(F)-[:default]->(G);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"B", _to:"E"}, {_from:"C", _to:"B"}, {_from:"C", _to:"D"}, {_from:"C", _to:"F"}, {_from:"D", _to:"B"}, {_from:"D", _to:"E"}, {_from:"F", _to:"D"}, {_from:"F", _to:"G"}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: topological_link_prediction
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | No | Specifies the first group of nodes for computation by their _id. If unset, all nodes in the graph are used as the first group of nodes. |
uuids |
[]_uuid |
/ | / | No | Specifies the first group of nodes for computation by their _uuid. If unset, all nodes in the graph are used as the first group of nodes. |
ids2 |
[]_id |
/ | / | No | Specifies the second group of nodes for computation by their _id. If unset, all nodes in the graph are used as the second group of nodes. |
uuids2 |
[]_uuid |
/ | / | No | Specifies the second group of nodes for computation by their _uuid. If unset, all nodes in the graph are used as the second group of nodes. |
type |
String | Common_Neighbors |
Adamic_Adar |
No | Specifies the similarity type; for Common Neighbors, keep it as Common_Neighbors. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
File Writeback
CALL algo.topological_link_prediction.write("my_hdc_graph", {
ids: ["C"],
ids2: ["A","E","G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}, {
file: {
filename: "cn"
}
})
algo(topological_link_prediction).params({
projection: "my_hdc_graph",
ids: ["C"],
ids2: ["A","E","G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}).write({
file: {
filename: "cn"
}
})
Result:
_id1,_id2,result
C,A,1
C,E,2
C,G,1
Full Return
CALL algo.topological_link_prediction.run("my_hdc_graph", {
ids: ["C"],
ids2: ["A","C","E","G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}) YIELD cn
RETURN cn
exec{
algo(topological_link_prediction).params({
ids: ["C"],
ids2: ["A","C","E","G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}) as cn
return cn
} on my_hdc_graph
Result:
| _id1 | _id2 | result |
|---|---|---|
| C | A | 1 |
| C | E | 2 |
| C | G | 1 |
Stream Return
CALL algo.topological_link_prediction.stream("my_hdc_graph", {
ids: ["C"],
ids2: ["A", "B", "D", "E", "F", "G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}) YIELD cn
FILTER cn.result >= 2
RETURN cn
exec{
algo(topological_link_prediction).params({
ids: ["C"],
ids2: ["A", "B", "D", "E", "F", "G"],
type: "Common_Neighbors",
return_id_uuid: "id"
}).stream() as cn
where cn.result >= 2
return cn
} on my_hdc_graph
Result:
| _id1 | _id2 | result |
|---|---|---|
| C | D | 2 |
| C | E | 2 |

