Overview
A topological sorting of a directed graph is an ordering of its nodes into a sequence, where the start node of every edge appears before its end node. Topological sorting is applicable only to directed acyclic graphs (DAGs) that do not contain any cycles.
Topological sorting has various applications in computer science and related fields. In project management and job scheduling, it plays a crucial role in determining the optimal order of task execution based on dependencies. It is also valuable in software development for resolving dependencies between modules, libraries, or components. By applying topological sorting, dependencies can be handled in the correct sequence, reducing the risk of conflicts and potential errors.
Concepts
Directed Acyclic Graph (DAG)
A directed acyclic graph (DAG) is a type of directed graph with no directed cycles. That is, it is not possible to start at any node v and follow a directed path to return back to v in a DAG.
As shown here, the first and second graphs are DAGs, while the third graph does contain a directed cycle (B→C→D→B) and therefore does not qualify as a DAG.
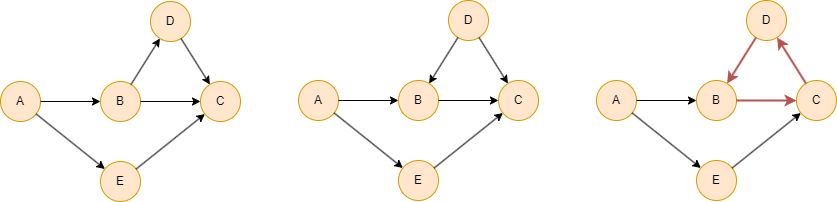
A directed graph is a DAG if and only if it can be topologically sorted.
Topological Sort
Every DAG has at least one topological sorting.
In the above examples, nodes in the first graph has 3 possible sortings:
- A, E, B, D, C
- A, B, E, D, C
- A, B, D, E, C
A DAG has a unique topological sorting if and only if it has a directed path containing all the nodes, in which case the sorting is the same as the order in which the nodes appear in the path.
In the following example, the nodes have only 1 possible topological sorting: A, B, D, C, E, F.
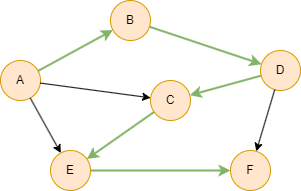
Considerations
Running the Topological Sort algorithm on a graph with cycles may result in some nodes being omitted. The omitted nodes are:
- Nodes that are part of a cycle (including self-cycles).
- Nodes that are reachable from the above nodes through outgoing edges.
In the given example, first is to omit nodes C, D and G, which form the cycle. Then, nodes F, J and H which are reachable from them are also omitted. As a result, the topological sorting result is A, I, B, E.
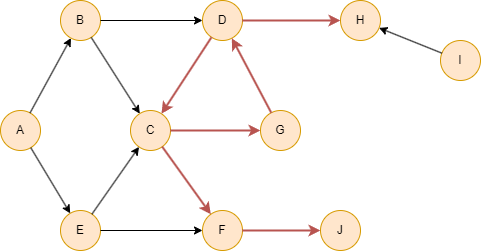
If a graph is disconnected, or becomes disconnected after omitting nodes that form the cycle and nodes influenced by them, topological sorting is performed within each connected component. The sorting results are then consistently returned for all components. Isolated nodes are also included and are not overlooked.
Example Graph
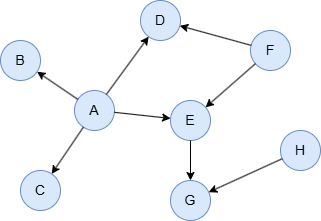
Run the following statements on an empty graph to define its structure and insert data:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(A)-[:default]->(B),
(A)-[:default]->(C),
(A)-[:default]->(D),
(A)-[:default]->(E),
(E)-[:default]->(G),
(F)-[:default]->(D),
(F)-[:default]->(E),
(H)-[:default]->(G);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"A", _to:"D"}, {_from:"A", _to:"E"}, {_from:"E", _to:"G"}, {_from:"F", _to:"D"}, {_from:"F", _to:"E"}, {_from:"H", _to:"G"}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: topological_sort
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results; this option is only valid in File Writeback. |
File Writeback
CALL algo.topological_sort.write("my_hdc_graph", {
return_id_uuid: "id"
}, {
file: {
filename: "sort"
}
})
algo(topological_sort).params({
projection: "my_hdc_graph",
return_id_uuid: "id"
}).write({
file: {
filename: "sort"
}
})
Result:
_id
F
H
A
B
C
D
E
G
Full Return
CALL algo.topological_sort.run("my_hdc_graph", {}) YIELD r
RETURN r
exec{
algo(topological_sort).params() as result
return result
} on my_hdc_graph
[{"id":"F","uuid":"2882304861028745219","schema":"default","values":{}}]
[{"id":"H","uuid":"3386708019294240772","schema":"default","values":{}}]
[{"id":"A","uuid":"10016006670783610881","schema":"default","values":{}}]
[{"id":"B","uuid":"3530823207370096641","schema":"default","values":{}}]
[{"id":"C","uuid":"12033619303845593090","schema":"default","values":{}}]
[{"id":"D","uuid":"288231475663339522","schema":"default","values":{}}]
[{"id":"E","uuid":"10520409829049106435","schema":"default","values":{}}]
[{"id":"G","uuid":"13690943966717935617","schema":"default","values":{}}]
Stream Return
CALL algo.topological_sort.stream("my_hdc_graph", {}) YIELD r
FOR node IN r
RETURN node._id
exec{
algo(topological_sort).params({}).stream() as r
uncollect r as node
return node._id
} on my_hdc_graph
Result:
| node._id |
|---|
| F |
| H |
| A |
| B |
| C |
| D |
| E |
| G |

