Overview

The SybilRank algorithm ranks the trust of nodes by early-terminated random walks in the network, typically Online Social Network (OSN). The surge in popularity of OSNs has accompanied by the increasing Sybil attacks, under which a malicious attacker creates multiple fake accounts (Sybils), with the purposes of spamming, distributing malware, manipulating votes or view counts for niche content, and so on.

SybilRank was proposed by Qiang Cao et al. in 2012, it is computationally efficient and can scale to large graphs.

• Q. Cao, M. Sirivianos, X. Yang, T. Pregueiro, Aiding the Detection of Fake Accounts in Large Scale Social Online Services (2012)

Concepts

Threat Model and Trust Seeds

SybilRank considers an OSN as an undirected graph, where each node corresponds to a user in the network, and each edge corresponds to a bilateral social relationship.

In the threat model of SybilRank, all nodes are divided into two disjoint sets: non-Sybils H, and Sybils S. Denote the non-Sybil region G_H as the subgraph induced by the set H, which includes all non-Sybils and edges among them. Similarly, the Sybil region G_S is the subgraph induced by S. G_H and G_S are connected by attacks edges between Sybils and non-Sybils.

Some nodes that are considered as non-Sybils are specified as trust seeds for the operation of SybilRank. Seeding trust on multiple nodes makes SybilRank robust to seed selection errors, as incorrectly designating a node that is Sybil or close to Sybils as a seed causes only a small fraction of the total trust to be initialized and propagated in the Sybil region.

Below is an example of the threat model with trust seeds:

An important assumption of SybilRank is that the number of attack edges is limited. Since SybilRank is designed for large scale attacks, where fake accounts are crafted and maintained at a low cost, and are thus unable to befriend many real users. It results in a sparse cut between G_H and G_S.

Early-Terminated Random Walk

In an undirected graph, if a random walk's transition probability to a neighbor node is uniformly distributed, when the number of steps is sufficient, the probability of landing at each node would converge to be proportional to its degree. The number of steps that a random walk needs to reach the stationary distribution is called the graph's mixing time.

SybilRank relies on the observation that an early-terminated random walk starting from a non-Sybil node (trust seed) has higher landing probability to land at a non-Sybil node than a Sybil node, as the walk is unlikely to traverse one of the relatively few attack edges. That is to say, there is a significant difference between the mixing time of the non-Sybil region G_H and the entire graph.

SybilRank refers to the landing probability of each node as the node’s trust. SybilRank ranks nodes according to their trust scores; nodes with low trust scores are ranked higher, and they are potential faker users.

Trust Propagation via Power Iteration

SybilRank uses the technique of power iteration to efficiently calculate the landing probability of random walks in large graphs. Power iteration involves successive matrix multiplications where each element of the matrix represents the random walk transition probability from one node to a neighbor node. Each iteration computes the landing probability distribution over all nodes as the random walk proceeds by one step.

In an undirected graph G = (V, E), initially a total trust T_G is evenly distributed among all trust seeds. During each power iteration, a node first evenly distributes its trust to its neighbors; it then collects trust distributed by its neighbors and updates its own trust accordingly. The trust of node v in the i-th iteration is:

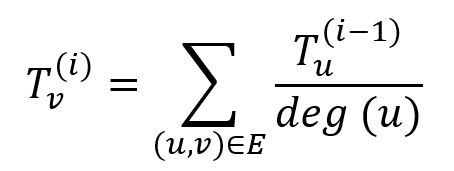
where node u belongs to the neighbor set of node v, deg(u) is the degree of node u. The total amount of trust T_G remains unchanged all the time.

With sufficient power iterations, the trust of all nodes would converge to the stationary distribution:

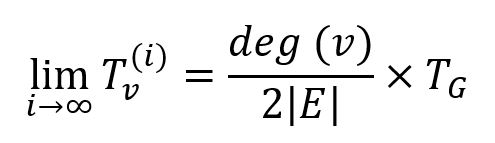
However, SybilRank terminates the power iteration after a number of steps before convergence, and it is suggested to be set as log2(|V|). This number of iterations is sufficient to reach an approximately stationary distribution of trust over the fast-mixing non-Sybil region G_H, but limits the trust escaping to the Sybil region G_S, thus non-Sybils will be ranked higher than Sybils.

In practice, the mixing time of G_H is affected by many factors, so log2(|V|) is only a reference, but it must be less than the mixing time of the whole graph.

Considerations

• Each self-loop adds two degrees to its subject node.
• The SybilRank algorithm ignores the direction of edges but calculates them as undirected edges.
• SybilRank’s computational cost is O(n log n). This is because each power iteration costs O(n), and it iterates O(log n) times. It is not related with the number of trust seeds.

Example Graph

To create this graph:

// Runs each row separately in order in an empty graphset
create().node_schema("user").edge_schema("link")
insert().into(@user).nodes([{_id:"H1"}, {_id:"H2"}, {_id:"H3"}, {_id:"H4"}, {_id:"H5"}, {_id:"H6"}, {_id:"H7"}, {_id:"H8"}, {_id:"H9"}, {_id:"H10"}, {_id:"S1"}, {_id:"S2"}, {_id:"S3"}, {_id:"S4"}])
insert().into(@link).edges([{_from:"S2", _to:"H4"}, {_from:"S3", _to:"H6"}, {_from:"S4", _to:"S2"}, {_from:"S4", _to:"S3"}, {_from:"S4", _to:"H9"}, {_from:"H1", _to:"H9"}, {_from:"H2", _to:"H7"}, {_from:"H2", _to:"H10"}, {_from:"H3", _to:"H1"}, {_from:"H3", _to:"H5"}, {_from:"H4", _to:"H3"}, {_from:"H4", _to:"H6"}, {_from:"H5", _to:"H1"}, {_from:"H6", _to:"H1"}, {_from:"H6", _to:"H3"}, {_from:"H6", _to:"H5"}, {_from:"H7", _to:"H10"}, {_from:"H8", _to:"H7"}])

Creating HDC Graph

To load the entire graph to the HDC server hdc-server-1 as hdc_sybilrank:

CALL hdc.graph.create("hdc-server-1", "hdc_sybilrank", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
})

hdc.graph.create("hdc_sybilrank", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: true
}).to("hdc-server-1")

Parameters

Algorithm name: sybil_rank

File Writeback

CALL algo.sybil_rank.write("hdc_sybilrank", {
  params: {
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4
  },
  return_params: {
    file: {
      filename: "sybil_rank"
    }
  }
})

algo(sybil_rank).params({
  projection: "hdc_sybilrank",
  return_id_uuid: "id",
  total_trust: 100,
  // Assigns H2, H3, and H5 as trust seeds
  trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
  loop_num: 4
}).write({
  file: {
    filename: "sybil_rank"
  }
})

Result:

_id,sybil_rank
S1,0
S4,3.61111
S2,4.45602
S3,4.71065
H9,5.0434
H8,5.09259
H4,6.66667
H10,7.87037
H5,8.67766
H1,9.59491
H2,9.9537
H7,10.4167
H3,11.305
H6,12.6013

DB Writeback

Writes the sybil_rank values from the results to the specified node property. The property type is float.

CALL algo.sybil_rank.write("hdc_sybilrank", {
  params: {
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4
  },
  return_params: {
    db: {
      property: "trust"
    }
  }
})

algo(sybil_rank).params({
  projection: "hdc_sybilrank",
  return_id_uuid: "id",
  total_trust: 100,
  // Assigns H2, H3, and H5 as trust seeds
  trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
  loop_num: 4
}).write({
  db:{ 
    property: 'trust'
  }
})

Full Return

CALL algo.sybil_rank("hdc_sybilrank", {
  params: {
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4
  },
  return_params: {}
}) YIELD trust
RETURN trust

exec{
  algo(sybil_rank).params({
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4
  }) as trust
  return trust
} on hdc_sybilrank

Result:

Stream Return

CALL algo.sybil_rank("hdc_sybilrank", {
  params: {
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4,
    limit: 4
  },
  return_params: {
  	stream: {}
  }
}) YIELD trust
RETURN trust

exec{
  algo(sybil_rank).params({
    return_id_uuid: "id",
    total_trust: 100,
    // Assigns H2, H3, and H5 as trust seeds
    trust_seeds: [8214567919347040258, 16429133639670824963, 15060039352950194181],
    loop_num: 4,
    limit: 4
  }).stream() as trust
  return trust
} on hdc_sybilrank

Result: