Overview
Node2Vec is a semi-supervised algorithm designed for feature learning of nodes in graphs, while efficiently preserving their neighborhood structure. It introduces a flexible search strategy that enables exploration of node neighborhoods using both BFS and DFS approaches. Additionally, it extends the Skip-gram model to graphs for training node embeddings. Node2Vec was proposed by A. Grover and J. Leskovec at Stanford University in 2016.
- A. Grover, J. Leskovec, node2vec: Scalable Feature Learning for Networks (2016)
Concepts
Node Similarity
Node2Vec learns a mapping of nodes into a low-dimensional vector space, aiming to ensure that similar nodes in the network exhibit close embeddings in the vector space.
Nodes in a network often alternate between two types of similarities:
1. Homophily
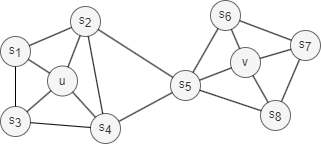
Homophily in networks refers to the tendency of nodes with similar properties, characteristics, or behaviors to be more likely connected or grouped into the same or similar communities (nodes u and s1 in the graph above belong to the same community).
For example, in social networks, people with similar backgrounds, interests, or opinions are more likely to form connections.
2. Structural Equivalence
Structural equivalence in networks refers to the concept that nodes are considered equivalent if they occupy similar structural roles. This means they share similar patterns of connections to other nodes, also known as similar local topology, regardless of their individual attributes. For example, nodes u and v in the graph above act as hubs within their respective communities, which indicates structural equivalence.
In social networks, structurally equivalent individuals may hold similar roles or positions within their groups, even if they are not directly connected.
Unlike homophily, structural equivalence does not require nodes to be adjacent or close in the network. Nodes can be far apart and still perform the same structural function.
There are two key points to keep in mind when discussing structural equivalence. First, perfect structural equivalence is uncommon in real-world networks, so the focus is often on measuring structural similarity. Second, as the neighborhood range being analyzed increases, the degree of structural similarity between two nodes tends to decrease.
Search Strategies
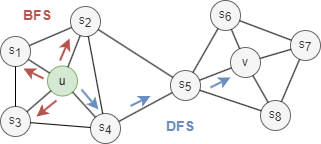
Generally, there are two extreme search strategies for generating a neighborhood set NS of k nodes:
- Breadth-first Search (BFS): NS is restricted to nodes which are immediate neighbors of the start node. E.g., NS(u) = s1, s2, s3 of size k = 3 in the graph above.
- Depth-first Search (DFS): NS consists of nodes sequentially searched at increasing distances from the start node. E.g., NS(u) = s4, s5, v of size k = 3 in the graph above.
BFS and DFS strategies play a key role in generating node embeddings that capture either homophily or structural equivalence:
- BFS samples nodes that are close to the starting node, resulting in embeddings that emphasize structural equivalence. This approach provides a detailed, microscopic view of the local neighborhood, which is often sufficient to characterize the local topology.
- DFS explores nodes farther from the starting node, producing embeddings that emphasize homophily. This broader, macro-level view of the neighborhood is useful for capturing community-level patterns and relationships based on shared properties or affiliations.
Node2Vec Framework
1. Node2Vec Walk
Node2Vec employs a biased random walk with the return parameter p and in-out parameter q to guide the walk.
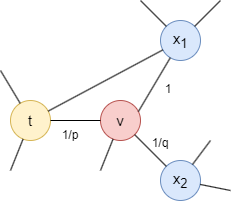
Consider a random walk that has just traversed edge (t,v) and arrived at node v. The next step is determined by the transition probabilities on edges (v,x) originating from v, which are proportional to the edge weights (which are 1 in unweighted graphs). The weights of edges (v,x) are adjusted using parameters p and q based on the shortest distance dtx between nodes t and x:
- If dtx = 0, the edge weight is scaled by
1/p. In the provided graph, dtt = 0. Parameterpinfluences the inclination to revisit the node just left. Whenp< 1, backtracking a step becomes more probable; whenp> 1, otherwise. - If dtx = 1, the edge weight remains unaltered. In the provided graph, dtx1 = 1.
- If dtx = 2, the edge weight is scaled by
1/q. In the provided graph, dtx2 = 2. Parameterqdetermines whether the walk moves inward (q> 1) or outward (q< 1).
Note that dtx must be one of {0, 1, 2}.
Through the two parameters, Node2Vec enables control over the trade-off between exploration and exploitation during random walk generation. This flexibility allows the algorithm to learn node representations that span a spectrum—from homophily to structural equivalence.
2. Node Embeddings
The node sequences generated from random walks serve as input to the Skip-gram model. SGD is used to optimize the model's parameters based on the prediction errors, and the model is optimized by techniques such as negative sampling and subsampling.
Considerations
- The Node2Vec algorithm treats all edges as undirected, ignoring their original direction.
Example Graph
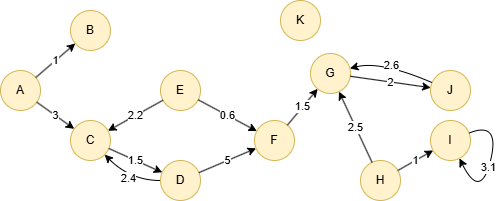
Run the following statements on an empty graph to define its structure and insert data:
ALTER EDGE default ADD PROPERTY {
score float
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(K:default {_id: "K"}),
(A)-[:default {score: 1}]->(B),
(A)-[:default {score: 3}]->(C),
(C)-[:default {score: 1.5}]->(D),
(D)-[:default {score: 2.4}]->(C),
(D)-[:default {score: 5}]->(F),
(E)-[:default {score: 2.2}]->(C),
(E)-[:default {score: 0.6}]->(F),
(F)-[:default {score: 1.5}]->(G),
(G)-[:default {score: 2}]->(J),
(H)-[:default {score: 2.5}]->(G),
(H)-[:default {score: 1}]->(I),
(I)-[:default {score: 3.1}]->(I),
(J)-[:default {score: 2.6}]->(G);
create().edge_property(@default, "score", float);
insert().into(@default).nodes([{_id:"A"},{_id:"B"},{_id:"C"},{_id:"D"},{_id:"E"},{_id:"F"},{_id:"G"},{_id:"H"},{_id:"I"},{_id:"J"},{_id:"K"}]);
insert().into(@default).edges([{_from:"A", _to:"B", score:1}, {_from:"A", _to:"C", score:3}, {_from:"C", _to:"D", score:1.5}, {_from:"D", _to:"C", score:2.4}, {_from:"D", _to:"F", score:5}, {_from:"E", _to:"C", score:2.2}, {_from:"E", _to:"F", score:0.6}, {_from:"F", _to:"G", score:1.5}, {_from:"G", _to:"J", score:2}, {_from:"H", _to:"G", score:2.5}, {_from:"H", _to:"I", score:1}, {_from:"I", _to:"I", score:3.1}, {_from:"J", _to:"G", score:2.6}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: node2vec
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | Yes | Specifies nodes to start random walk by their _id. If unset, computation includes all nodes. |
uuids |
[]_uuid |
/ | / | Yes | Specifies nodes to start random walk by their _uuid. If unset, computation includes all nodes. |
walk_length |
Integer | ≥1 | 1 |
Yes | Depth of each walk, i.e., the number of nodes to visit. |
walk_num |
Integer | ≥1 | 1 |
Yes | Number of walks to perform for each specified node. |
p |
Float | >0 | 1 |
Yes | The return parameter; a larger value reduces the probability of returning. |
q |
Float | >0 | 1 |
Yes | The in-out parameter; it tends to walk at the same level when the value is greater than 1, otherwise it tends to walk far away. |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | Yes | Specifies numeric edge properties used as weights by summing their values. Only properties of numeric type are considered, and edges without these properties are ignored. |
window_size |
Integer | ≥1 | / | No | The maximum size of context. |
dimension |
Integer | ≥2 | / | No | Dimensionality of the embeddings. |
loop_num |
Integer | ≥1 | / | No | Number of training iterations. |
learning_rate |
Float | (0,1) | / | No | Learning rate used initially for training the model, which decreases after each training iteration until reaches min_learning_rate. |
min_learning_rate |
Float | (0,learning_rate) |
/ | No | Minimum threshold for the learning rate as it is gradually reduced during the training. |
neg_num |
Integer | ≥1 | 5 |
Yes | Number of negative samples to produce for each positive sample, it is suggested to set between 1 to 10. |
resolution |
Integer | ≥1 | 1 |
Yes | The parameter used to enhance negative sampling efficiency; a higher value offers a better approximation to the original noise distribution; it is suggested to set as 10, 100, etc. |
sub_sample_alpha |
Float | / | 0.001 |
Yes | The factor affecting the probability of down-sampling frequent nodes; a higher value increases this probability; a value ≤0 means not to apply subsampling |
min_frequency |
Integer | / | / | No | Nodes that appear less times than this threshold in the training "corpus" will be excluded from the "vocabulary" and disregarded in the embedding training; a value ≤0 means to keep all nodes. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both values to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
File Writeback
CALL algo.node2vec.write("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}, {
file: {
filename: "embeddings"
}
})
algo(node2vec).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}).write({
file:{
filename: 'embeddings'
}
})
_id,embedding_result
J,0.0800537,0.0883881,-0.0766052,-0.0655609,0.0273315,
D,0.0604218,0.0188171,0.00422668,-0.0720703,0.0443695,
F,-0.0871277,0.0249908,-0.0150269,-0.0191437,-0.0663147,
H,-0.0376434,0.0515869,0.0605072,0.0593811,0.0319489,
B,0.030896,-0.0760529,-0.0819153,0.0993927,0.0760254,
A,0.0618011,-0.0120789,0.0803131,-0.0098999,0.0146942,
E,-0.00298462,-0.0596649,0.0262451,-0.0267487,-0.0765076,
K,0.0950836,0.0875854,-0.0219025,-0.0045227,0.0101837,
C,-0.0727539,-0.0801422,0.091095,0.00126038,-0.0516479,
I,-0.0608429,-0.0615295,0.0339386,0.00402832,0.0266205,
G,-0.0842712,-0.0761566,-0.0026001,0.0228729,0.0509949,
DB Writeback
Writes the embedding_result values from the results to the specified node property. The property type is float[].
CALL algo.node2vec.write("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}, {
db: {
property: "vector"
}
})
algo(node2vec).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}).write({
db: {
property: "vector"
}
})
Full Return
CALL algo.node2vec.run("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) YIELD embeddings
RETURN embeddings
exec{
algo(node2vec).params({
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) as embeddings
return embeddings
} on my_hdc_graph
Result:
_id |
embedding_result |
|---|---|
| J | [0.100067138671875,0.11048507690429688,-0.09575653076171875,-0.08195114135742188] |
| D | [0.0341644287109375,0.07552719116210938,0.02352142333984375,0.005283355712890625] |
| F | [-0.090087890625,0.055461883544921875,-0.10890960693359375,0.031238555908203125] |
| H | [-0.0187835693359375,-0.023929595947265625,-0.08289337158203125,-0.047054290771484375] |
| B | [0.064483642578125,0.07563400268554688,0.07422637939453125,0.039936065673828125] |
| A | [0.0386199951171875,-0.09506607055664063,-0.10239410400390625,0.12424087524414063] |
| E | [0.09503173828125,0.07725143432617188,-0.01509857177734375,0.10039138793945313] |
| K | [-0.0123748779296875,0.018367767333984375,-0.00373077392578125,-0.07458114624023438] |
| C | [0.032806396484375,-0.033435821533203125,-0.09563446044921875,0.11885452270507813] |
| I | [0.1094818115234375,-0.027378082275390625,-0.00565338134765625,0.012729644775390625] |
| G | [-0.0909423828125,-0.10017776489257813,0.11386871337890625,0.001575469970703125] |
Stream Return
CALL algo.node2vec.stream("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) YIELD embeddings
RETURN embeddings
exec{
algo(node2vec).params({
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
p: 0.5,
q: 1000,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) as embeddings
return embeddings
} on my_hdc_graph
Result:
_id |
embedding_result |
|---|---|
| J | [0.08005370944738388,0.08838806301355362,-0.07660522311925888,-0.06556091457605362,0.02733154222369194] |
| D | [0.06042175367474556,0.01881713792681694,0.0042266845703125,-0.07207031548023224,0.04436950758099556] |
| F | [-0.087127685546875,0.02499084547162056,-0.015026855282485485,-0.01914367638528347,-0.066314697265625] |
| H | [-0.0376434326171875,0.05158691480755806,0.06050720065832138,0.05938110500574112,0.03194885328412056] |
| B | [0.03089599683880806,-0.07605285942554474,-0.08191528171300888,0.09939269721508026,0.07602538913488388] |
| A | [0.06180114671587944,-0.01207885704934597,0.08031310886144638,-0.009899902157485485,0.0146942138671875] |
| E | [-0.0029846192337572575,-0.05966491624712944,0.0262451171875,-0.0267486572265625,-0.076507568359375] |
| K | [0.09508361667394638,0.08758544921875,-0.02190246619284153,-0.0045227049849927425,0.01018371619284153] |
| C | [-0.07275390625,-0.08014221489429474,0.091094970703125,0.0012603759532794356,-0.05164794996380806] |
| I | [-0.06084289401769638,-0.06152953952550888,0.03393859788775444,0.0040283203125,0.02662048302590847] |
| G | [-0.08427123725414276,-0.0761566162109375,-0.0026000975631177425,0.0228729248046875,0.050994873046875] |

