Overview
The Label Propagation algorithm (LPA) is a community detection method based on label propagation. Initially, each node is assigned a label. During each iteration, every node updates its label to the one most common among its neighbors. Through this iterative process, densely connected groups of nodes tend to reach a consensus on a shared label, with nodes sharing the same label ultimately forming a community.
LPA does not optimize any specific predefined measure of community quality, nor does it require the number of communities to be specified in advance. Instead, it relies purely on the network's structure to guide the progression. Its simplicity makes LPA highly efficient for analyzing large and complex networks.
Related material of the algorithm:
- U.N. Raghavan, R. Albert, S. Kumara, Near linear time algorithm to detect community structures in large-scale networks (2007)
Concepts
Label
Label of a node is initialized with a specified property value or its unique UUID.
Nodes sharing the same label at the end of the algorithm are considered members of the same community.
Label Propagation
In the simplest setting, at each propagation iteration, a node updates its label to the one held by the largest number of its neighbors.
For example, in the diagram below, the blue node’s label will change from d to c.
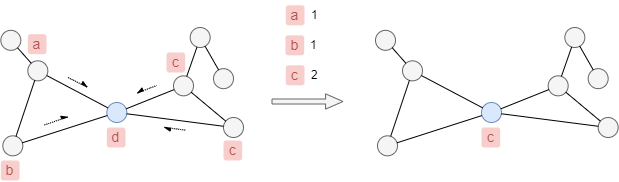
When node and edge weights are considered, the label weight is calculated as the sum of the products of corresponding node and edge weights. In this case, each node updates its label to the one with the highest total weight.
As the weights of nodes and edges shown in the example below, the label of the blue node will be updated from d to a.
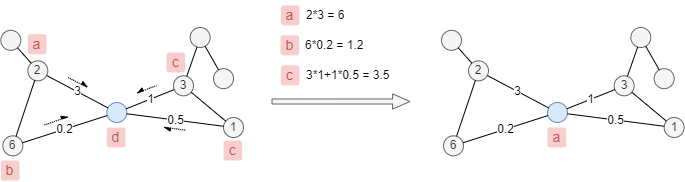
Multi-label Propagation
In multi-label propagation, each node can hold multiple labels simultaneously. In this case, each label is assigned a label probability proportional to its weight, while the sum of all label probabilities for each node equals 1.
In the example below, each node keeps 2 labels with their probabilities written next to them. The labels of the blue node will be updated from d, c to a, c with label probabilities Pa = 6.3/(6.3+1.85) = 0.77 and Pc = 1.85/(6.3+1.85) = 0.23.
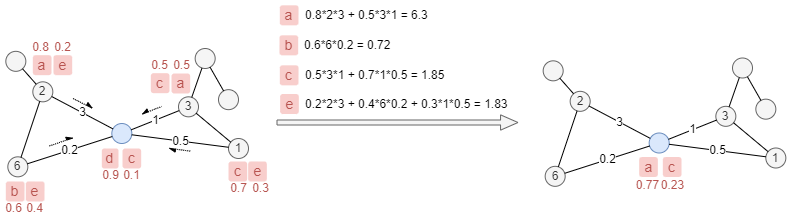
Considerations
- The LPA algorithm treats all edges as undirected, ignoring their original direction.
- A Node with self-loops propagates its current label(s) to itself, with each self-loop counted twice.
- The LPA algorithm follows a synchronous update principle, where all nodes update their labels simultaneously based on their neighbors' current labels. However, in some cases—especially in bipartite graphs—label oscillations may occur. To address this issue, LPA incorporates an interrupt mechanism that detects and prevents excessive oscillations.
- Due to factors such as the order of nodes, the random selection among labels with equal weights and parallel computations, the community detection results of LPA may vary between runs.
Example Graph
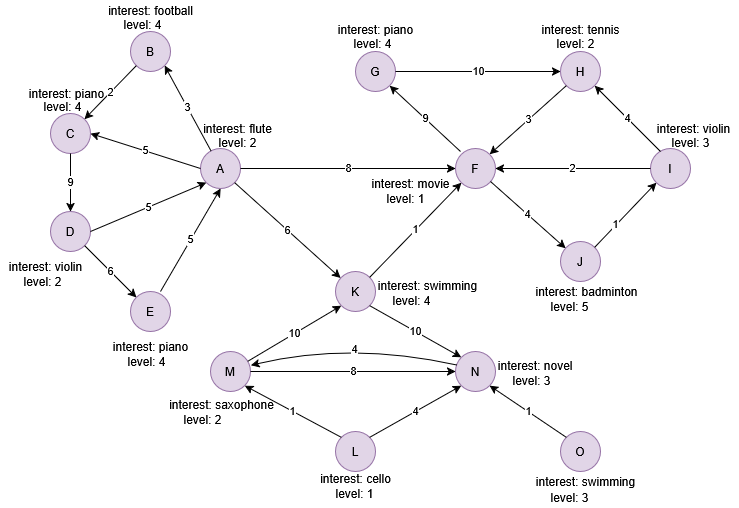
Run the following statements on an empty graph to define its structure and insert data:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
user ({interest string, level int32})
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
connect ()-[{strength int32}]->()
};
INSERT (A:user {_id:"A",interest:"flute",level:2}),
(B:user {_id:"B",interest:"football",level:4}),
(C:user {_id:"C",interest:"piano",level:4}),
(D:user {_id:"D",interest:"violin",level:2}),
(E:user {_id:"E",interest:"piano",level:4}),
(F:user {_id:"F",interest:"movie",level:1}),
(G:user {_id:"G",interest:"piano",level:4}),
(H:user {_id:"H",interest:"tennis",level:2}),
(I:user {_id:"I",interest:"violin",level:3}),
(J:user {_id:"J",interest:"badminton",level:5}),
(K:user {_id:"K",interest:"swimming",level:4}),
(L:user {_id:"L",interest:"cello",level:1}),
(M:user {_id:"M",interest:"saxophone",level:2}),
(N:user {_id:"N",interest:"novel",level:3}),
(O:user {_id:"O",interest:"swimming",level:3}),
(A)-[:connect {strength:3}]->(B),
(A)-[:connect {strength:5}]->(C),
(A)-[:connect {strength:8}]->(F),
(A)-[:connect {strength:6}]->(K),
(B)-[:connect {strength:2}]->(C),
(C)-[:connect {strength:9}]->(D),
(D)-[:connect {strength:5}]->(A),
(D)-[:connect {strength:6}]->(E),
(E)-[:connect {strength:5}]->(A),
(F)-[:connect {strength:9}]->(G),
(F)-[:connect {strength:4}]->(J),
(G)-[:connect {strength:10}]->(H),
(H)-[:connect {strength:3}]->(F),
(I)-[:connect {strength:2}]->(F),
(I)-[:connect {strength:4}]->(H),
(J)-[:connect {strength:1}]->(I),
(K)-[:connect {strength:1}]->(F),
(K)-[:connect {strength:10}]->(N),
(L)-[:connect {strength:1}]->(M),
(L)-[:connect {strength:4}]->(N),
(M)-[:connect {strength:10}]->(K),
(M)-[:connect {strength:8}]->(N),
(N)-[:connect {strength:4}]->(M),
(O)-[:connect {strength:1}]->(N);
create().node_schema("user").edge_schema("connect");
create().node_property(@user,"interest",string).node_property(@user,"level",int32).edge_property(@connect,"strength",int32);
insert().into(@user).nodes([{_id:"A",interest:"flute",level:2}, {_id:"B",interest:"football",level:4}, {_id:"C",interest:"piano",level:4}, {_id:"D",interest:"violin",level:2}, {_id:"E",interest:"piano",level:4}, {_id:"F",interest:"movie",level:1}, {_id:"G",interest:"piano",level:4}, {_id:"H",interest:"tennis",level:2}, {_id:"I",interest:"violin",level:3}, {_id:"J",interest:"badminton",level:5}, {_id:"K",interest:"swimming",level:4}, {_id:"L",interest:"cello",level:1}, {_id:"M",interest:"saxophone",level:2}, {_id:"N",interest:"novel",level:3}, {_id:"O",interest:"swimming",level:3}]);
insert().into(@connect).edges([{_from:"A",_to:"B",strength:3}, {_from:"A",_to:"C",strength:5}, {_from:"A",_to:"F",strength:8}, {_from:"A",_to:"K",strength:6}, {_from:"B",_to:"C",strength:2}, {_from:"C",_to:"D",strength:9}, {_from:"D",_to:"A",strength:5}, {_from:"D",_to:"E",strength:6}, {_from:"E",_to:"A",strength:5}, {_from:"F",_to:"G",strength:9}, {_from:"F",_to:"J",strength:4}, {_from:"G",_to:"H",strength:10}, {_from:"H",_to:"F",strength:3}, {_from:"I",_to:"H",strength:4}, {_from:"I",_to:"F",strength:2}, {_from:"J",_to:"I",strength:1}, {_from:"K",_to:"F",strength:1}, {_from:"K",_to:"N",strength:10}, {_from:"L",_to:"M",strength:1}, {_from:"L",_to:"N",strength:4}, {_from:"M",_to:"N",strength:8}, {_from:"M",_to:"K",strength:10}, {_from:"N",_to:"M",strength:4}, {_from:"O",_to:"N",strength:1}]);
Running on HDC Graphs
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: lpa
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
node_label_property |
"<@schema.?><property>" |
/ | / | Yes | Specifies numeric or string node property used to initialize node labels; nodes without the specified property are ignored. The system will generate the labels if it is unset. |
node_weight_property |
"<@schema.?><property>" |
/ | / | Yes | Numeric node property used as the node weights. |
edge_weight_property |
"<@schema.?><property>" |
/ | / | Yes | Numeric edge property used as the edge weights. |
loop_num |
Integer | ≥1 | 5 |
Yes | Number of propagation iterations. |
k |
Integer | ≥1 | 1 |
Yes | Specifies the maximum number of labels to keep for each node at the end of the computation, with all labels sorted by probability in descending order. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
File Writeback
CALL algo.lpa.write("my_hdc_graph", {
return_id_uuid: "id",
k: 2,
loop_num: 5,
edge_weight_property: 'strength'
}, {
file: {
filename: "lpa"
}
})
algo(lpa).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
k: 2,
loop_num: 5,
edge_weight_property: 'strength'
}).write({
file: {
filename: "lpa"
}
})
DB Writeback
Writes each label_<N> and the corresponding probability_<N> from the results to the specified node properties. The property types are string and float, respectively.
CALL algo.lpa.write("my_hdc_graph", {
node_label_property: 'interest',
k: 2,
loop_num: 10
}, {
db: {
property: "lab"
}
})
algo(lpa).params({
projection: "my_hdc_graph",
node_label_property: 'interest',
k: 2,
loop_num: 10
}).write({
db: {
property: "lab"
}
})
The label and label probability of each node is written to new properties lab_1, probability_1, lab_2, and probability_2.
Stats Writeback
CALL algo.lpa.write("my_hdc_graph", {
node_label_property: 'interest',
k: 2,
loop_num: 10
}, {
stats: {}
})
algo(lpa).params({
projection: "my_hdc_graph",
node_label_property: 'interest',
k: 2,
loop_num: 10
}).write({
stats:{}
})
Result:
| label_count |
|---|
| 6 |
Full Return
CALL algo.lpa.run("my_hdc_graph", {
return_id_uuid: "id",
node_label_property: "@user.interest",
k: 2
}) YIELD r
RETURN r
exec{
algo(lpa).params({
return_id_uuid: "id",
node_label_property: "@user.interest",
k: 2
}) as r
return r
} on my_hdc_graph
Result:
| _id | label_1 | probability_1 | label_2 | probability_2 |
|---|---|---|---|---|
| I | badminton | 0.517124 | movie | 0.482876 |
| G | movie | 0.563411 | badminton | 0.436589 |
| J | movie | 0.605133 | badminton | 0.394867 |
| D | piano | 0.701716 | flute | 0.298284 |
| N | swimming | 0.675096 | saxophone | 0.324904 |
| F | badminton | 0.564691 | movie | 0.435309 |
| H | movie | 0.535167 | badminton | 0.464833 |
| B | piano | 0.646695 | flute | 0.353305 |
| L | novel | 0.510868 | swimming | 0.489132 |
| A | piano | 0.736380 | flute | 0.263620 |
| O | novel | 0.765123 | swimming | 0.234877 |
| E | piano | 0.594943 | flute | 0.405057 |
| K | novel | 0.510868 | swimming | 0.489132 |
| M | novel | 0.515860 | swimming | 0.484140 |
| C | piano | 0.640369 | flute | 0.359631 |
Stream Return
CALL algo.lpa.stream("my_hdc_graph", {
return_id_uuid: "id",
node_label_property: "@user.interest",
node_weight_property: "@user.level",
edge_weight_property: "strength",
loop_num: 10
}) YIELD r
RETURN r.label_1 AS label, count(r) GROUP BY label
exec{
algo(lpa).params({
return_id_uuid: "id",
node_label_property: "@user.interest",
node_weight_property: "@user.level",
edge_weight_property: "strength",
loop_num: 10
}).stream() as r
group by r.label_1 as label
return table(label, count(r))
} on my_hdc_graph
Result:
| label | count(r) |
|---|---|
| violin | 3 |
| tennis | 2 |
| swimming | 3 |
| novel | 2 |
| piano | 5 |
Stats Return
CALL algo.lpa.stats("my_hdc_graph", {
node_label_property: "interest",
edge_weight_property: "strength",
k: 1,
loop_num: 5
}) YIELD s
RETURN s
exec{
algo(lpa).params({
node_label_property: "interest",
edge_weight_property: "strength",
k: 1,
loop_num: 5
}).stats() as s
return s
} on my_hdc_graph
Result:
| label_count |
|---|
| 5 |
Running on Distributed Projections
Creating Distributed Projection
To project the entire graph to its shard servers as myProj:
CREATE PROJECTION myProj OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
}
create().projection("myProj", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
})
Parameters
Algorithm name: lpa
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
node_label_property |
"<@schema.?><property>" |
/ | / | Yes | Numeric or string node property used to initialize node labels; nodes without the specified property are ignored. The system will generates the labels if it is unset. |
node_weight_property |
"<@schema.?><property>" |
/ | / | Yes | Numeric node property used as the node weights. |
edge_weight_property |
"<@schema.?><property>" |
/ | / | Yes | Numeric edge property used as the edge weights. |
loop_num |
Integer | ≥1 | 5 |
Yes | Number of propagation iterations. |
File Writeback
CALL algo.lpa.write("myProj", {
loop_num: 5,
edge_weight_property: 'strength'
}, {
file: {
filename: "lpa"
}
})
algo(lpa).params({
projection: "myProj",
loop_num: 5,
edge_weight_property: 'strength'
}).write({
file: {
filename: "lpa"
}
})
DB Writeback
Writes each label_<N> and the corresponding probability_<N> from the results to the specified node properties. The property types are string and float, respectively.
CALL algo.lpa.write("myProj", {
node_label_property: 'interest',
loop_num: 10
}, {
db: {
property: "lab"
}
})
algo(lpa).params({
projection: "myProj",
edge_schema_property: 'score'
}).write({
db:{
property: 'lpa'
}
})

