Overview
Fast Random Projection (or FastRP) is a scalable and efficient algorithm for learning node representations in a graph. It computes node embeddings iteratively through two main steps: first, constructing a node similarity matrix; second, reducing dimension using random projection.
FastRP was proposed by H. Chen et al. in 2019:
- H. Chen, S.F. Sultan, Y. Tian, M. Chen, S. Skiena, Fast and Accurate Network Embeddings via Very Sparse Random Projection (2019)
FastRP Framework
The authors of FastRP observe that most network embedding methods follow a common two-step pattern: (1) construct a node similarity matrix or implicitly sample node pairs from it, and (2) apply dimension reduction techniques to obtain embeddings.
Regarding the dimension reduction, many popular algorithms, like Node2Vec, rely on time-consuming methods such as Skip-gram. The authors argue that the effectiveness of these methods should be attributed to the quality of the similarity matrix, rather than the dimension reduction method employed.
Based on this insight, FastRP utilizes very sparse random projection, a scalable, optimization-free method for dimension reduction.
Very Sparse Random Projection
Random projection is a dimension reduction method that approximately preserves pairwise distances between data points when embedding them from a high-dimensional space to a lower-dimensional space. Its theoretical foundation is primarily based on the Johnson-Lindenstrauss Lemma.
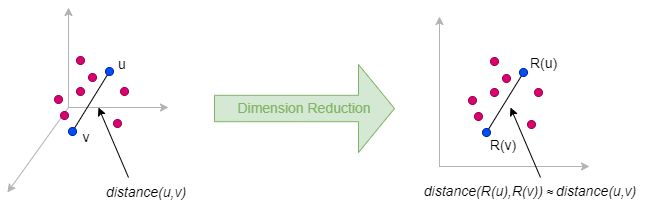
The idea behind random projection is very simple: to reduce a matrix Mn×m (with n = m for graph data) to a lower-dimensional matrix Nn×d where d ≪ n, we multiply M by a random projection matrix Rm×d: N = M ⋅ R**.
The matrix R is generated by independently sampling its entries from a random distribution. Specifically, FastRP uses very sparse random projection for dimension reduction, where each entry of R is sampled from the following distribution:

and s=sqrt(m).
Very sparse random projection offers high computational efficiency, as it requires only matrix multiplication and (1-1/s) of the entries of R are zero.
Additionally, Ultipa supports initializing the matrix R with a combination of some selected numeric node properties (features). In this case, each row of matrix R is formed by concatenating two parts:

- Elements d1 ~ dx are generated by the Very Sparse Random Projection algorithm.
- Elements p1 ~ py is a linear combination of the selected node property values.
- The total embedding dimension is x + y, where y is referred to as the property dimension.
- The number of selected node features does not need to be the same as the property dimension.
Node Similarity Matrix Construction
FastRP keeps two key features when constructing the node similarity matrix:
- Preserve high-order proximity in the graph
- Apply element-wise normalization to the matrix
Let S be the adjacency matrix of graph G =(V,E), D be the degree matrix, and A be the transition matrix and A = D-1S. In the example below, the number on each edge represents the edge weight:

In the transition matrix A, the entry Aij represents the probability of reaching node j from node i in a 1-step random walk. Furthermore, raising A to the k-th power yields the matrix Ak, where each entry Akij denotes the probability of reaching node j from node i in exactly k steps of random walk. Therefore, the matrix Ak preserves high-order proximity between nodes in the graph.
However, as k → ∞, it can be proved that Akij → dj/2m, where m = |E| and dj is the degree of the j-th node. Since many real-world graphs are scale-free, the entries in Ak follow a heavy-tailed distribution. This implies that the pairwise distances between data points in Ak are predominantly influenced by columns with exceptionally large values. This skews the similarity and reduces effectiveness of the subsequent dimension reduction step.
To address this, FastRP applies an additional normalization step to the matrix Ak by multiplying it with a diagonal normalization matrix L, where each diagonal entry is defined as Lij = (dj/2m)β, and β is the normalization strength. The parameter β controls the influence of node degree on the embeddings: when β is negative, the importance of high-degree neighbors is weakened; when β is positive, their importance is amplified.
Algorithm Process
The FastRP algorithm follows these steps:
- Generate the random projection matrix R.
- Reduce the dimension of the normalized 1-step transition matrix: N1 = A ⋅ L ⋅ R
- Reduce the dimension of the normalized 2-step transition matrix: N2 = A ⋅ (A ⋅ L ⋅ R) = A ⋅ N1
- Repeat step 3 until the normalized k-step transition matrix: Nk = A ⋅ Nk-1
- Generate the weighted combination of different powers of A: N = α1N1 + ... + αkNk, where α1,...,αk are the iteration weights.
The efficiency of FastRP also benefits from the associative property of matrix multiplication. Instead of computing Ak from scratch, it updates the result iteratively using previous results.
Considerations
- The FastRP algorithm treats all edges as undirected, ignoring their original direction.
Example Graph
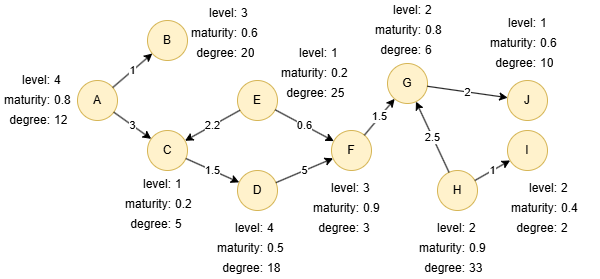
Run the following statements on an empty graph to define its structure and insert data:
ALTER NODE default ADD PROPERTY {
level uint32, maturity float, degree uint32
};
ALTER EDGE default ADD PROPERTY {
score float
};
INSERT (A:default {_id: "A", level: 4, maturity: 0.8, degree: 12}),
(B:default {_id: "B", level: 3, maturity: 0.6, degree: 20}),
(C:default {_id: "C", level: 1, maturity: 0.2, degree: 5}),
(D:default {_id: "D", level: 4, maturity: 0.5, degree: 18}),
(E:default {_id: "E", level: 1, maturity: 0.2, degree: 25}),
(F:default {_id: "F", level: 3, maturity: 0.9, degree: 3}),
(G:default {_id: "G", level: 2, maturity: 0.8, degree: 6}),
(H:default {_id: "H", level: 2, maturity: 0.9, degree: 33}),
(I:default {_id: "I", level: 2, maturity: 0.4, degree: 2}),
(J:default {_id: "J", level: 1, maturity: 0.6, degree: 10}),
(A)-[:default {score: 1}]->(B),
(A)-[:default {score: 3}]->(C),
(C)-[:default {score: 1.5}]->(D),
(D)-[:default {score: 5}]->(F),
(E)-[:default {score: 2.2}]->(C),
(E)-[:default {score: 0.6}]->(F),
(F)-[:default {score: 1.5}]->(G),
(G)-[:default {score: 2}]->(J),
(H)-[:default {score: 2.5}]->(G),
(H)-[:default {score: 1}]->(I);
create().node_property(@default, "level", uint32).node_property(@default, "maturity", float).node_property(@default, "degree", uint32).edge_property(@default, "score", float);
insert().into(@default).nodes([{_id:"A", level:4, maturity:0.8, degree:12},{_id:"B", level:3, maturity:0.6, degree:20},{_id:"C", level:1, maturity:0.2, degree:5},{_id:"D", level:4, maturity:0.5, degree:18},{_id:"E", level:1, maturity:0.2, degree:25},{_id:"F", level:3, maturity:0.9, degree:3},{_id:"G", level:2, maturity:0.8, degree:6},{_id:"H", level:2, maturity:0.9, degree:33},{_id:"I", level:2, maturity:0.4, degree:2},{_id:"J", level:1, maturity:0.6, degree:10}]);
insert().into(@default).edges([{_from:"A", _to:"B", score:1}, {_from:"A", _to:"C", score:3}, {_from:"C", _to:"D", score:1.5}, {_from:"D", _to:"F", score:5}, {_from:"E", _to:"C", score:2.2}, {_from:"E", _to:"F", score:0.6}, {_from:"F", _to:"G", score:1.5}, {_from:"G", _to:"J", score:2}, {_from:"H", _to:"G", score:2.5}, {_from:"H", _to:"I", score:1}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: fastRP
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
dimension |
Integer | ≥2 | / | No | Dimensionality of the embeddings. |
normalizationStrength |
Float | / | / | Yes | The normalization strength β . |
iterationWeights |
[]Float | ≥0 | [0.0,1.0,1.0] |
Yes | Weight for each iteration, the size of the array is the number of iterations. |
edge_schema_property |
[]"@<schema>?.<property>" |
/ | / | Yes | Specifies numeric edge properties used as weights by summing their values. Only properties of numeric type are considered, and edges without these properties are ignored. |
node_schema_property |
[]"@<schema>?.<property>" |
/ | / | Yes | Numeric node properties used as features; propertyDimension and node_schema_property should be configured together or both unset. |
propertyDimension |
Integer | (0,dimension] |
/ | Yes | Length of the property dimension; propertyDimension and node_schema_property should be configured together or both unset. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both values to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
File Writeback
CALL algo.fastRP.write("my_hdc_graph", {
return_id_uuid: "id",
dimension: 5,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}, {
file: {
filename: "embeddings"
}
})
algo(fastRP).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
dimension: 5,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}).write({
file:{
filename: 'embeddings'
}
})
_id,embedding_result
J,-1.12587,-1.20511,-1.12587,0.079247,0.079247,
D,-1.11528,-1.22975,-1.11528,0,0,
F,-1.1547,-1.1547,-1.1547,0,0,
H,-1.07893,-1.15311,-1.22729,0,0,
B,-1.1547,-1.1547,-1.1547,0,0,
A,-1.1547,-1.1547,-1.1547,0,0,
E,-1.12083,-1.12083,-1.21962,0,0,
C,-1.24807,-1.24807,-0.394019,-0.854049,0,
I,-1.1547,-1.1547,-1.1547,0,0,
G,-0.538663,-1.54159,-1.04013,-0.501465,0,
DB Writeback
Writes the embedding_result values from the results to the specified node property. The property type is float[].
CALL algo.fastRP.write("my_hdc_graph", {
return_id_uuid: "id",
dimension: 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}, {
db: {
property: "vector"
}
})
algo(fastRP).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
dimension: 10,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 1],
edge_schema_property: 'score',
node_schema_property: ['level', 'maturity', 'degree'],
propertyDimension: 2
}).write({
db: {
property: "vector"
}
})
Full Return
CALL algo.fastRP.run("my_hdc_graph", {
return_id_uuid: "id",
dimension: 3,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}) YIELD embeddings
RETURN embeddings
exec{
algo(fastRP).params({
return_id_uuid: "id",
dimension: 3,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}) as embeddings
return embeddings
} on my_hdc_graph
Result:
_id |
embedding_result |
|---|---|
| J | [0.0,2.299999952316284,0.0] |
| D | [0.0,-2.299999952316284,0.0] |
| F | [0.0,0.0,2.299999952316284] |
| H | [-2.299999952316284,0.0,0.0] |
| B | [-2.299999952316284,0.0,0.0] |
| A | [-1.6263456344604492,0.0,-1.6263456344604492] |
| E | [0.0,2.299999952316284,0.0] |
| C | [0.0,0.0,0.0] |
| I | [1.6263456344604492,1.6263456344604492,0.0] |
| G | [0.0,0.0,0.0] |
Stream Return
CALL algo.fastRP.stream("my_hdc_graph", {
return_id_uuid: "id",
dimension: 4,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}) YIELD embeddings
RETURN embeddings
exec{
algo(fastRP).params({
return_id_uuid: "id",
dimension: 4,
normalizationStrength: 1.5,
iterationWeights: [0, 0.8, 0.2, 0.3, 1]
}).stream() as embeddings
return embeddings
} on my_hdc_graph
Result:
_id |
embedding_result |
|---|---|
| J | [0.0,-1.6263456344604492,0.0,-1.6263456344604492] |
| D | [1.6263456344604492,0.0,0.0,1.6263456344604492] |
| F | [0.0,0.0,-2.299999952316284,0.0] |
| H | [1.6263456344604492,0.0,0.0,-1.6263456344604492] |
| B | [0.0,-2.299999952316284,0.0,0.0] |
| A | [-1.6263456344604492,-1.6263456344604492,0.0,0.0] |
| E | [0.0,0.0,0.0,-2.299999952316284] |
| C | [0.0,1.6263456344604492,0.0,1.6263456344604492] |
| I | [0.0,0.0,0.0,0.0] |
| G | [-1.3279056549072266,0.0,-1.3279056549072266,1.3279056549072266] |

