Overview
The single-source shortest path (SSSP) problem involves finding the shortest paths from a given source node to all other reachable nodes in a graph. In weighted graphs, the shortest path minimizes the total edge weights; in unweighted graphs, it minimizes the number of edges (hops). The cost or distance of a path refers to this total weight or count.
The Delta-Stepping algorithm is a parallelizable variant of Dijkstra's algorithm, designed to improve performance on large graphs by dividing work into manageable steps.
Related material of the algorithm:
- U. Meyer, P. Sanders, Δ-Stepping: A Parallel Single Source Shortest Path Algorithm (1998)
Concepts
Delta-Stepping Single-Source Shortest Path
The Delta-Stepping Single-Source Shortest Path (SSSP) algorithm introduces the concept of "buckets" and performs relaxation operations in a more coarse-grained manner. The algorithm utilizes a positive real number parameter delta (Δ) to achieve the following:
- Maintain an array B of buckets such that B[i] contains nodes whose distance falls within the range [iΔ, (i+1)Δ). Thus Δ is also called the "step width" or "bucket width".
- Distinguish between light edges with weight ≤ Δ and heavy edges with weight > Δ in the graph. Light-edge nodes are prioritized during relaxation as they have lower weights and are more likely to yield shorter paths.
The term relaxation refers to the process of updating the distance of a node v that is connected to node u to a potential shorter distance by considering the path through node u. Specifically, the distance of node v is updated to dist(v) = dist(u) + w(u,v), where w(u,v) is the weight of the edge (u,v). This update is performed only if the current dist(v) is greater than dist(u) + w(u,v).
In the Delta-Stepping SSSP algorithm, the relaxation also includes assigning the relaxed node to the corresponding bucket based on its updated distance value.
Below is the description of the basic Delta-Stepping SSSP algorithm, along with an example to compute the weighted shortest paths in an undirected graph starting from the source node b, and Δ is set to 3:
1. At the begining of the algorithm, all nodes are assigned an initial distance of infinity, except for the source node, which is set to 0. The source node is then placed into bucket B[0].
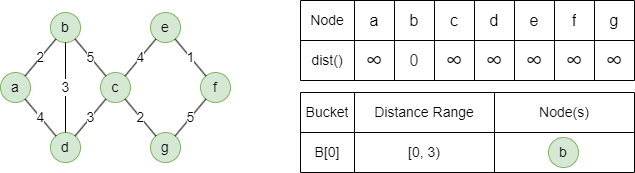
2. In each iteration, remove all nodes from the first nonempty bucket B[i]:
- Relax all light-edge neighbors of the removed nodes, the relaxed nodes might be assigned to B[i] or B[i+1]; defer the relaxation of the heavy-edge neighbors.
- If B[i] is refilled, repeat the above operation until B[i] is empty.
- Relax all deferred heavy-edge neighbors.

Relax light-edge neighbors a with dist(a) = min(0+2,∞) = 2, and d with dist(b) = min(0+3,∞) = 3.

Light-edge neighbor b cannot be relaxed.
Relax heavy-edge neighbor c with dist(c) = min(0+5,∞) = 5, d cannot be relaxed.
3. Repeat step 2 until all buckets are empty.
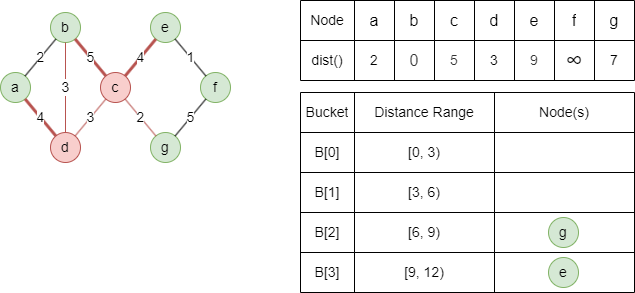
Relax light-edge neighbor g with dist(g) = min(5+2,∞) = 7, b, c and d cannot be relaxed.
Relax heavy-edge neighbor e with dist(e) = min(5+4,∞) = 9, a and b cannot be relaxed.
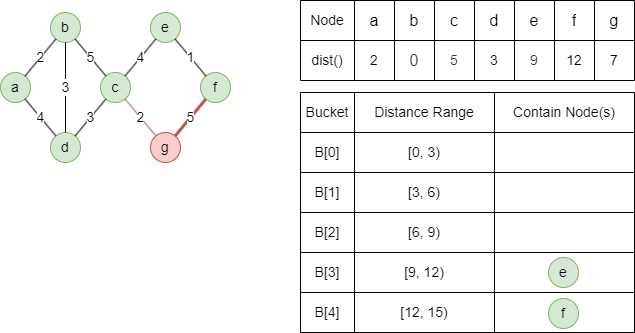
Light-edge neighbor c cannot be relaxed.
Relax heavy-edge neighbor f with dist(f) = min(7+5,∞) = 12.
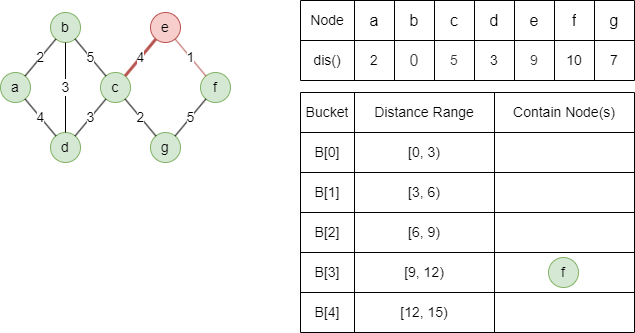
Relax light-edge neighbor f with dist(f) = min(9+1,12) = 10.
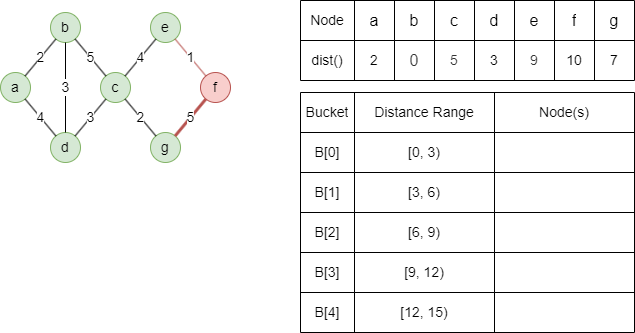
Light-edge neighbor e cannot be relaxed.
Heavy-edge neighbor g cannot be relaxed.
The algorithm ends here since all buckets are empty.
By dividing nodes into buckets and processing them in parallel, the Delta-Stepping algorithm efficiently leverages available computational resources, making it well-suited for large-scale graphs and parallel computing environments.
Considerations
- The Delta-Stepping SSSP algorithm is only applicable to graphs with non-negative edge weights. If negative weights are present, the Delta-Stepping SSSP algorithm might produce false results. In this case, a different algorithm like the SPFA should be used.
- If multiple shortest paths exist between two nodes, the algorithm will find all of them.
- In disconnected graphs, the algorithm only outputs the shortest paths from the source node to all nodes belonging to the same connected component as the source node.
Example Graph
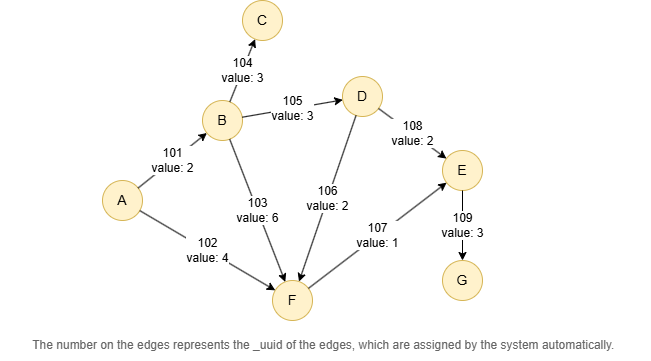
Run the following statements on an empty graph to define its structure and insert data:
ALTER EDGE default ADD PROPERTY {
value int32
};
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(A)-[:default {value: 2}]->(B),
(A)-[:default {value: 4}]->(F),
(B)-[:default {value: 3}]->(C),
(B)-[:default {value: 3}]->(D),
(B)-[:default {value: 6}]->(F),
(D)-[:default {value: 2}]->(E),
(D)-[:default {value: 2}]->(F),
(E)-[:default {value: 3}]->(G),
(F)-[:default {value: 1}]->(E);
create().edge_property(@default, "value", int32);
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}]);
insert().into(@default).edges([{_from:"A", _to:"B", value:2}, {_from:"A", _to:"F", value:4}, {_from:"B", _to:"F", value:6}, {_from:"B", _to:"C", value:3}, {_from:"B", _to:"D", value:3}, {_from:"D", _to:"F", value:2}, {_from:"F", _to:"E", value:1}, {_from:"D", _to:"E", value:2}, {_from:"E", _to:"G", value:3}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: sssp
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
_id |
/ | / | No | Specifies a single source node by its _id. |
uuids |
_uuid |
/ | / | No | Specifies a single source node by its _uuid. |
direction |
String | in, out |
/ | Yes | Specifies that the shortest paths should only contain incoming edges (in) or outgoing edges (out); edge direction is ignored if it is unset. |
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | Yes | Specifies numeric edge properties used as weights by summing their values. Only properties of numeric type are considered, and edges without these properties are ignored. |
record_path |
Integer | 0, 1 |
0 |
Yes | Whether to include the shortest paths in the results; sets to 1 to return the totalCost and the shortest paths, or to 0 to return the totalCost only. |
impl_type |
String | delta_stepping |
beta |
No | Specifies the implementation type of the SSSP algorithm; for the Delta-Stepping SSSP, keep it as delta_stepping; beta is Ultipa's default shortest path algorithm. |
delta |
Float | >0 | 2 |
Yes | The value of delta; only valid when impl_type is set to delta_stepping. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. Edges can only be represented by _uuid. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
order |
String | asc, desc |
/ | Yes | Sorts the results by totalCost. |
File Writeback
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: "@default.value",
impl_type: "delta_stepping",
return_id_uuid: "id"
}, {
file: {
filename: "costs"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: "@default.value",
impl_type: "delta_stepping",
return_id_uuid: "id"
}).write({
file: {
filename: "costs"
}
})
Result:
_id,totalCost
G,8
D,5
F,4
B,2
E,5
C,5
CALL algo.sssp.write("my_hdc_graph", {
ids: "A",
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
delta: 2,
record_path: 1,
return_id_uuid: "id"
}, {
file: {
filename: "paths"
}
})
algo(sssp).params({
projection: "my_hdc_graph",
ids: "A",
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
delta: 2,
record_path: 1,
return_id_uuid: "id"
}).write({
file: {
filename: "paths"
}
})
Result:
totalCost,_ids
8,A--[102]--F--[107]--E--[109]--G
5,A--[101]--B--[105]--D
5,A--[102]--F--[107]--E
5,A--[103]--B--[104]--C
4,A--[102]--F
2,A--[101]--B
Full Return
CALL algo.sssp.run("my_hdc_graph", {
ids: 'A',
edge_schema_property: 'value',
impl_type: 'delta_stepping',
delta: 3,
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: 'value',
impl_type: 'delta_stepping',
delta: 3,
record_path: 0,
return_id_uuid: 'id',
order: 'desc'
}) as r
return r
} on my_hdc_graph
Result:
| _id | totalCost |
|---|---|
| G | 8 |
| D | 5 |
| E | 5 |
| C | 5 |
| F | 4 |
| B | 2 |
Stream Return
CALL algo.sssp.stream("my_hdc_graph", {
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
record_path: 1,
return_id_uuid: 'id'
}) YIELD r
RETURN r
exec{
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
impl_type: 'delta_stepping',
record_path: 1,
return_id_uuid: 'id'
}).stream() as r
return r
} on my_hdc_graph
Result:
totalCost |
_ids |
|---|---|
| 8 | ["A","102","F","107","E","109","G"] |
| 5 | ["A","101","B","105","D"] |
| 5 | ["A","102","F","107","E"] |
| 5 | ["A","101","B","104","C"] |
| 4 | ["A","102","F"] |
| 2 | ["A","101","B"] |

