✓ File Writeback ✕ Property Writeback ✓ Direct Return ✓ Stream Return ✕ Stats

Overview

CELF (Cost Effective Lazy Forward) algorithm is used to select some seed nodes in a network as propagation source to reach as many nodes as possible. This is known as Influence Maximization (IM), where 'influence' represents anything that can be spread across the network, such as contamination, information, disease, etc.

CELF was proposed by Jure Leskovec et al. in 2007, it improves the traditional Greedy algorithm based on the IC model by taking advantage of the submodularity. It only calculates the spread score for all nodes only at the initial stage and does not recalculate for all nodes afterwards, hence cost-effective.

Related materials of the algorithm:

• J. Leskovec, A. Krause, C. Guestrin, C. Faloutsos, J. VanBriesen, N. Glance, Cost-effective Outbreak Detection in Networks (2007)
• D. Kempe, J. Kleinberg, E. Tardos, Maximizing the Spread of Influence through a Social Network (2003)

A typical application of the algorithm is to prevent epidemic outbreak by selecting a small group of people to monitor, so that any disease can be detected in an early stage.

Concepts

Spread Function - Independent Cascade

This algorithm adopts Independent Cascade (IC) model to simulate the influence spread process in the network. IC is a probabilistic model, it starts with a set of active seed nodes, and in step k:

• For each node that becomes active in step k-1, it has a single chance to activate each inactive outgoing neighbor with a success probability.
• The process runs until no more activations are possible.

The spread of the given seed set is measured by the number of active nodes in the graph when it ends. This process is repeated for a large number of time (Monte Carlo Simulations) and we calculate it by taking the average.

Submodularity

The spread function IC() is called submodular as the marginal gain of a single node v is diminishing as the seed set S grows:

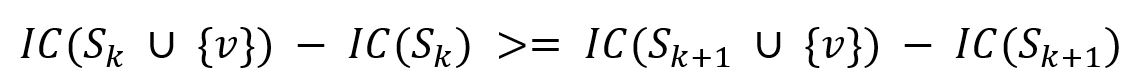
where the seed set |S_k+1| > |S_k|, S ∪ {v} means to add node v into the seed set.

Submodularity of the spread function is the key property exploited by CELF. CELF significantly improves the traditional Greedy algorithm that is used to solve the influence maximization problem, it runs a lot faster while achieving near optimal results.

Lazy Forward

When CELF begins, like Greedy, it calculates the spread for each node, puts them in a list sorted by the descending spread. As the seed set is empty now, the spread for each node can be viewed as its initial marginal gain.

In the first iteration, the top node is moved from the list to the seed set.

In the next iteration, only calculate the marginal gain for the current top node. After sorting, if that node remains at top, move it to the seed set; if not, repeat the process for the new top node.

Unlike Greedy, CELF avoids calculating marginal gain for all the rest nodes in each iteration, this is where the submodularity of the spread function is considered - the marginal gain of every node in this round is always lower than the previous round. So if the top node remains at top, we can put it into the seed set directly without calculating for other nodes.

The algorithm stops when the seed set reaches the set size.

Syntax

• Command: algo(celf)
• Parameters:

Examples

The example graph is as follows:

File Writeback

algo(celf).params({
  seedSetSize: 3,
  monteCarloSimulations: 1000,
  propagationProbability: 0.5 
}).write({
  file:{
    filename: "seeds"
  }
})

Results: File seeds

I,4.777
F,5.746
H,6.333

Direct Return

algo(celf).params({
  seedSetSize: 2,
  monteCarloSimulations: 1000,
  propagationProbability: 0.6 
}) as seeds
return seeds

Results: seeds

Stream Return

Example: Select 3 seeds from the graph, return their ID, created time and spread

algo(celf).params({
  seedSetSize: 3,
  monteCarloSimulations: 1000,
  propagationProbability: 0.6 
}).stream() as seeds
find().nodes({_uuid == seeds._uuid}) as nodes
return table(nodes._id, nodes.createdOn, seeds.spread)

Results: table(nodes._id, nodes.createdOn, seeds.spread)