Ultipa has recently released v4.0 of its flagship graph database product, on top of its v3.0’s already world-leading performance. Ultipa 4.0 introduced performance improvements of 50% with a 30% reduction in memory usage.

In a 2022 benchmark test using Twitter-2010 dataset (42M vertices and 1.47B edges), Ultipa shows (see Benchmark Report) great performance advantage over other graph systems (Neo4j, Tigergraph, and ArangoDB) using a typical 3-instance PC-server cluster. Very consistent benchmarking/stress-testing results have been achieved using any kind of commercial or academic/public datasets:

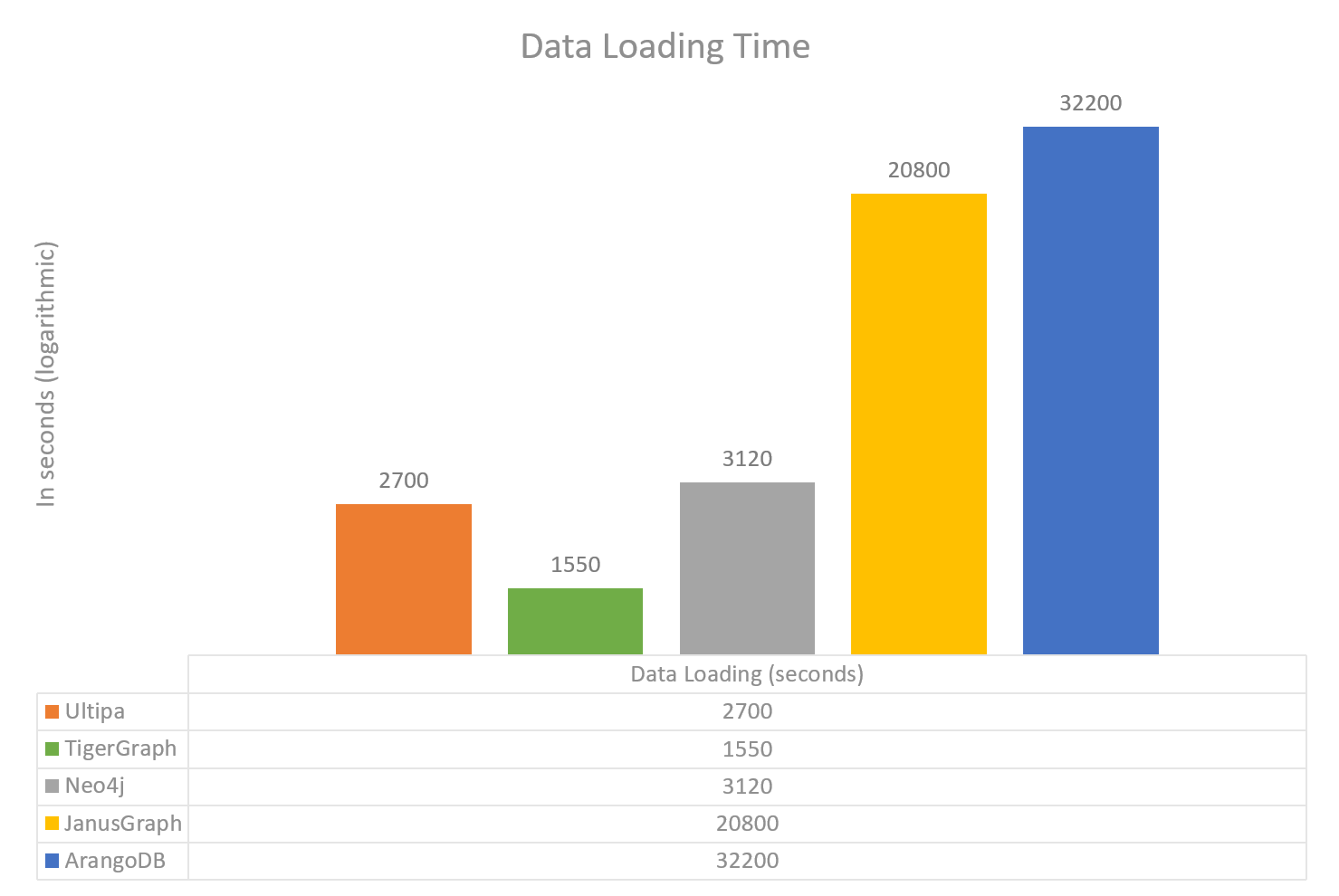
• Data Ingestion: Ultipa is 1-12 times faster than most of other graph databases.
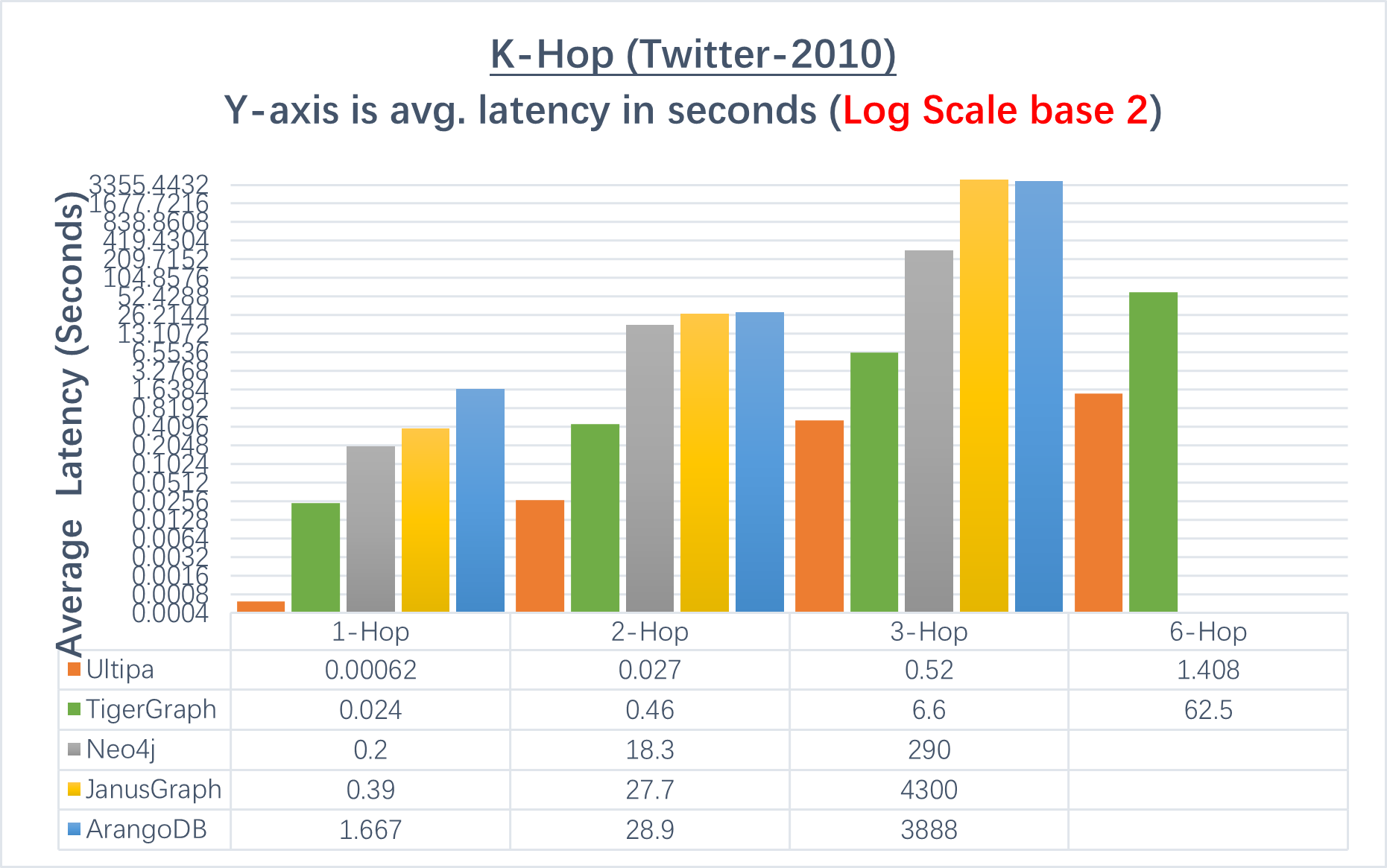
• K-Hop or Shortest Path: Ultipa is 10-1,000 times faster than any other graph database. For ultra-deep (>6 hops) queries, Ultipa is the only system that can return with correct results.
• Graph Algorithms (PageRank, LPA, Louvain, Jaccard Similarity, Random Walk, etc.): Ultipa is at least 10 times faster while some systems couldn’t return at all.

Loading Test

Loading the entire dataset into graph database and start providing services. This test can show how fast a graph system ingest large-volume of data.

K-Hop Neighbor Querying

K-hop query is a fundamental type of query with any graph system. It allows user to quickly identify the scope of impact of an entity (the subject vertex). K-hop must be implemented using BFS (Breadth-First-Search) method, and there are a few caveats:

• There are usually 2 ways of defining K-Hop and the results are different. One way is all neighbors from the 1st hop all the way to the Kth hop, the other way is the neighbors exactly Kth-Hop away from the starting vertex.

• If a vertex appears on the Nth Hop of a specific vertex, it will NOT appear on any other hop. While executing the algorithm, it’s pivotal to conduct de-duplication of vertices across different hops, otherwise, the results would be wrong.

• Number of a vertex’s immediate neighbors are NOT the same as the number of edges, because a pair of connecting vertices may have 2 edges connecting them bi-directionally.

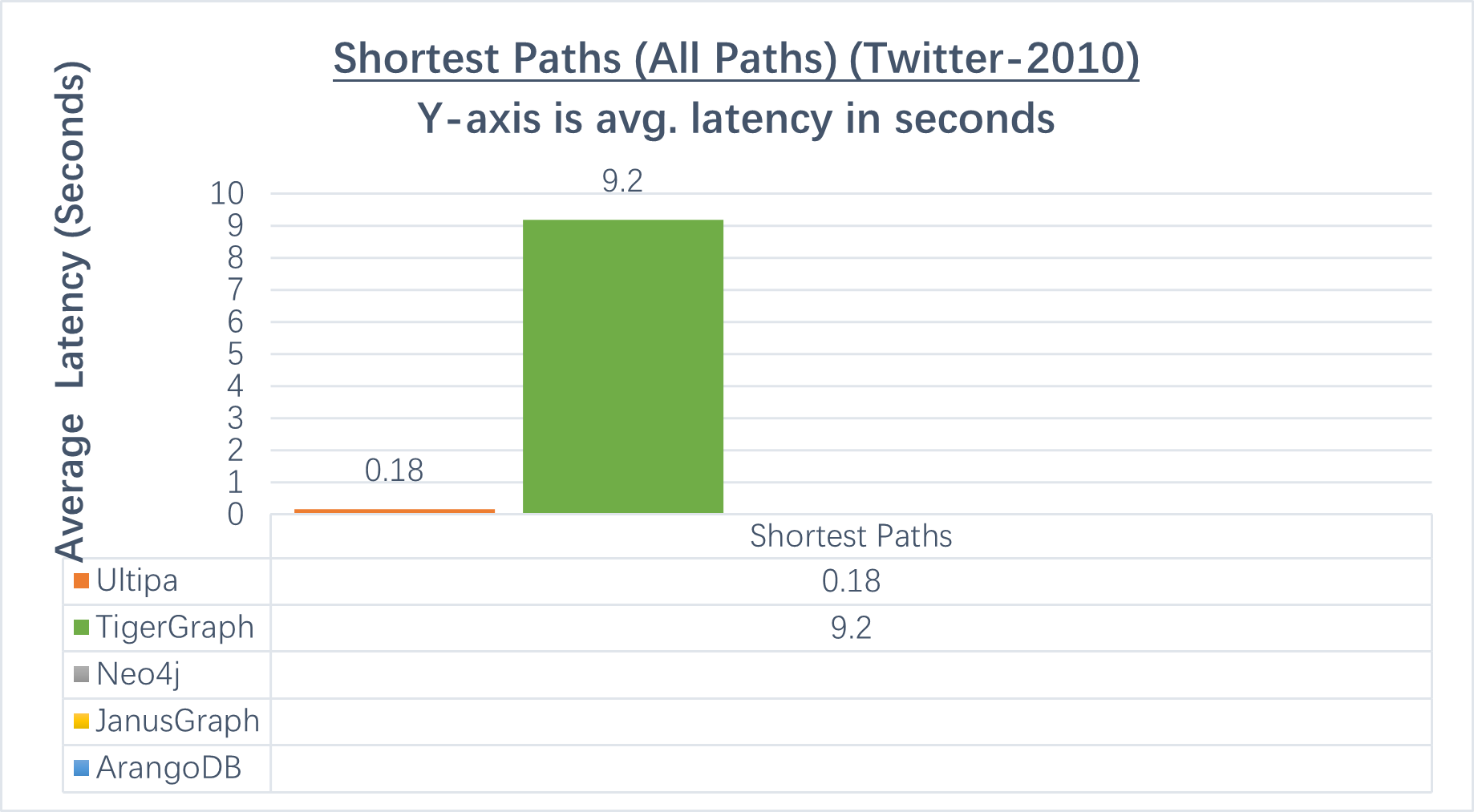
Shortest Paths

Finding shortest paths is a fundamental type of graph query. Like K-hop query, it is also implanted using BFS method, namely breadth-first search. The caveat with Shortest Path finding is that there are usually multiple paths instead of one, some graph systems can NOT return the correct number of paths due to faulty implementation. It’s often more challenging to query for shortest paths on large dataset like Twitter, therefore it’s meaningful to examine how swiftly a graph system can run this query.

The objective of this test is to find all shortest paths between any pair of nodes and log the execution time and total number of paths.

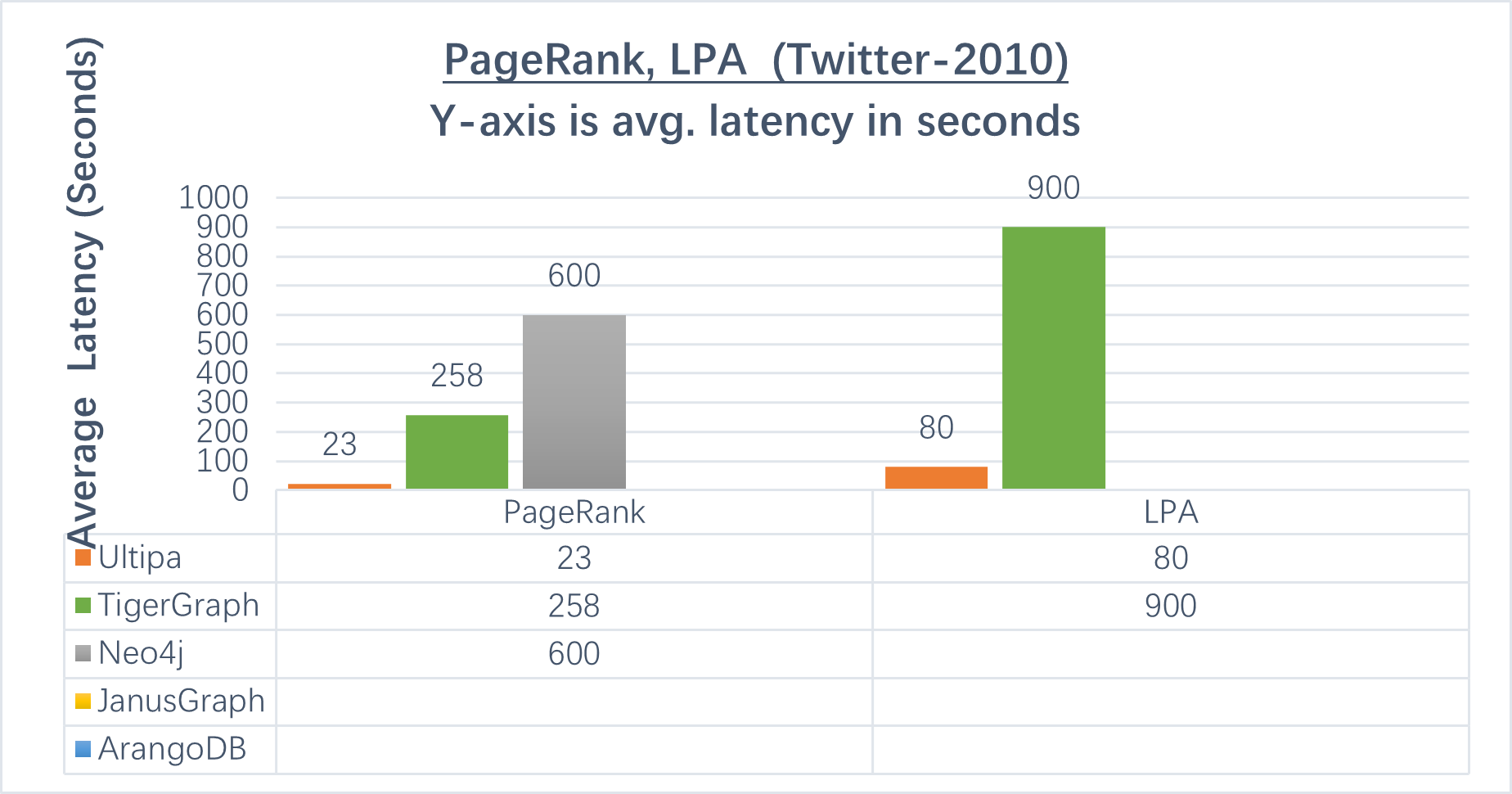
PageRank

PageRank is an algorithm used by Google Search to rank web pages in their search engine results. As of September 24, 2019, PageRank and all associated patents are expired. PageRank algorithm is useful in many use cases, for example to find the most influential or popular members of a particular group of users.

It is imperative that PageRank algorithm should be conducted in an iterative fashion that traverses all nodes and edges. Some graph databases, by default, do this wrongly. Neo4j is one such example, it allows running the algorithm on limited number of vertices instead of on ALL the vertices. On the other hand, returning results in an ordered way is useful in determining the top-ranked pages (nodes or entities), unfortunately, many graph systems do NOT support result-ranking natively.

Ultipa performances are the best, also considering that only Ultipa returns the PageRank results in an ordered way, which is more time consuming. In the cart below, systems that do not carry a result couldn’t finish the algorithm.

Click here or scan the QR code below to see more and updated benchmarks on Ultipa web site: