What is Graph Embedding?
Graph embedding is a technique that produces the latent vector representations for graphs. Graph embedding can be performed in different levels of the graph, the two predominant levels are:
- Node Embeddings - Map each node in a graph to a vector.
- Graph Embeddings - Map the whole graph to a vector.
Each vector yielded from this process is also referred to as an embedding or representation.
The term "latent" suggests that these vectors are inferred or learned from the data. They are created in a way that preserves the structure (how nodes are connected) and/or attributes (node and edge properties) within the graph, which might not be immediately apparent.
Taking node embeddings as example, nodes that are more similar in the graph will have vectors that are closer to each other in the vector space.
To provide an illustration, below shows the results (on the right) of running node embedding algorithm DeepWalk to the Zachary's karate club graph (on the left). In the graph, the colors of the nodes indicate modularity-based clustering. Once all the nodes have been transformed into two-dimensional vectors, it becomes evident that nodes within the same community are positioned relatively closer to each other.
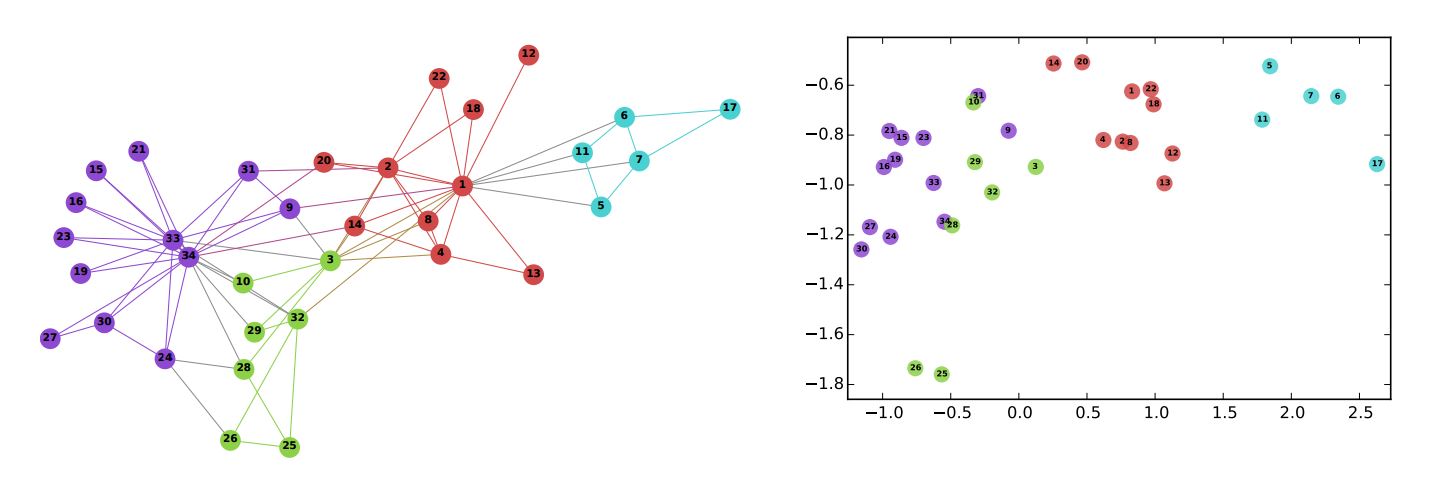B. Perozzi, et al., DeepWalk: Online Learning of Social Representations (2014)Closeness of the Embeddings
The notion of closeness among the embeddings generally refers to how near the vectors representing nodes or other graph elements are in the embedding space. In essence, embeddings that exhibit spatial proximity in the vector space are indicative of a degree of similarity within the original graph.
In practice, gauging the closeness of embeddings involves employing diverse distance or similarity metrics, such as Euclidean Distance and Cosine Similarity.
Embedding Dimension
The choice of the embedding dimension, also known as the embedding size or vector size, depends on factors such as data complexity, specific tasks, and computational resources. While there is no one-size-fits-all answer, a typical range of embedding dimensions in practice falls between 50 and 300.
Smaller embeddings facilitate faster computations and comparisons. A recommended approach is to begin with a smaller dimension and progressively expand it as needed, relying on experimentation and validation against performance metrics pertinent to your application.
Why Graph Embedding?
Dimensionality Reduction
Graphs are often deemed high-dimensional due to the complex relationships they encapsulate, rather than the physical dimensions they occupy.
Graph embedding functions as a dimensionality reduction method that strives to capture the most important information from graph data while substantially reducing the complexity and computational challenges associated with high dimensions. Within the realm of dimensionality reduction and embedding, even a few hundred dimensions are still labeled as low-dimensional relative to the original high-dimensional data.
Enhanced Compatibility in Data Science
Vector spaces offer dozens of advantages over graphs in terms of seamless integration with mathematical and statistical approaches within the field of data science. Conversely, graphs, constituted by nodes and edges, are confined to employing only specific subsets of these methodologies.
The inherent advantage of vectors lies in their innate suitability for mathematical operations and statistical techniques, as each vector embodies a composite of numerical features. Basic operations like addition and dot products manifest with simplicity and computational efficiency in vector spaces. This efficiency frequently translates into swifter computations when contrasted with analogous operations performed on graphs.
How Graph Embedding is Used?
Graph embedding serves as a bridge, acting as a preprocessing step for graphs. Once we generate embeddings for nodes, edges, or graphs, we can leverage these embeddings for various downstream tasks. These tasks include node classification, graph classification, link prediction, clustering and community detection, visualization, and more.
Graph Analytics
We have a bunch of graph algorithms cater to diverse graph analysis purposes. While they offer valuable insights, they do have limitations. Often reliant on handcrafted features extracted from adjacency matrices, these algorithms might not entirely capture intricate data nuances. Furthermore, efficiently executing these algorithms on large-scale graphs demands significant computational effort.
This is where graph embedding comes to play. By creating low-dimensional representations, embeddings provide richer and more adaptable inputs for a wide spectrum of analyses and tasks. These learned vectors bolster the efficiency and accuracy of graph analytics, outperforming direct execution within the high-dimensional graph domain.
Consider the case of node similarity analysis. Conventional similarity algorithms generally fall into two categories: neighborhood-based similarity and property-based similarity. The former, exemplified by Jaccard Similarity and Overlap Similarity, relies on the 1-hop neighborhood of nodes and compute similarity scores. The latter, represented by Euclidean Distance and Cosine Similarity, uses multiple numeric node properties to calculate the similarity scores based on property values.
While these methods have their merits, they often capture only surface-level node features, thus limiting their applicability. In contrast, embedding nodes with latent and advanced information from the graph enriches the input data for these similarity algorithms. This fusion empowers the algorithms to consider more sophisticated relationships, leading to more meaningful analyses.
Machine Learning & Deep Learning
Contemporary machine learning (ML) and deep learning (DL) techniques have revolutionized various domains. Yet, applying them directly to graphs presents unique challenges. Graphs possess characteristics distinct from traditional structured data (e.g., tabular data), making them less amenable to standard ML/DL methods.
Although there are ways to apply ML/DL to graphs, graph embedding proves a simple and effective method. By converting graphs or graph elements into continuous vectors, embeddings not only abstract the complexities of arbitrary graph sizes and dynamic topologies, but also harmonize well with modern ML/DL toolsets and libraries.
However, turning data into a digestible format for ML/DL is not enough. Feature learning is also a significant challenge before inputting data into ML/DL models. Traditional feature engineering is both time-consuming and less accurate. Embeddings, serving as learned features encapsulating both structural and attribute information, amplify the model's comprehension of the data.
Imagine a social network where nodes represent individuals and edges depict social connections. The task is to predict individuals' political affiliation. A traditional approach might involve extracting handcrafted features such as the number of friends, average age of friends, and education level of neighbors for each individual. These features would be then fed into a ML model like a decision tree or random forest. However, this approach fails to capture all the data's nuances, treating each individual's social connections as separate features and disregarding the intricate relationships within the graph.
In contrast, utilizing graph embeddings enables the creation of more sophisticated integrations for each individual, yielding accurate and context-aware predictions.