Overview
Struc2Vec, short for "structure to vector", is an algorithm that generates node embeddings while preserving the graph's structural properties. It focuses on capturing topological similarities between nodes, enabling structurally similar nodes to have similar vector representations.
- L. Ribeiro, P. Saverese, D. Figueiredo, struc2vec: Learning Node Representations from Structural Identity (2017)
While Node2Vec captures a certain degree of structural similarity among nodes, it is limited by the depth of random walks used during the generation process.Struc2Vec, on the other hand, overcomes this limitation by explicitly preserving structural roles, ensuring that nodes with similar topological characteristics are positioned closely in the embedding space.
The choice between Node2Vec and Struc2Vec depends on the nature of downstream tasks:
- Node2Vec is better suited for tasks that emphasize node homophily, capturing similarity in attributes and connections.
- Struc2Vec is ideal for tasks that focus on local topology similarity, preserving the structural relationships among nodes.
Concepts
Structural Similarity
In various networks, nodes often exhibit distinct structural identities that reflect their specific functions or roles. Nodes that perform similar functions naturally belong to the same class, signifying a high degree of structural similarity. For instance, in a company's social network, all interns might exhibit similar structural roles.
Structural similarity implies that the neighborhood topologies of such nodes are homogenous or symmetrical. In other words, nodes with similar functions tend to have analogous patterns of connections and relationships with their neighbors.

As illustrated here, nodes u and v are structurally similar—they have degrees of 5 and 4, are connected to 3 and 2 triangles respectively, and each connects to the rest of the network through 2 nodes. Despite not sharing a direct link or common neighbor, and possibly being far apart in the graph, they still exhibit similar structural roles.
However, when the distance between such nodes exceeds the walk depth, methods like Node2Vec struggle to generate similar representations for them. This limitation is effectively addressed by the Struc2Vec algorithm.
Struc2Vec Framework
1. Measure structural similarity
Intuitively, two nodes with the same degrees are considered structurally similar. If their neighbors also share the same degrees, the structural similarity between the two nodes becomes even stronger.
Consider an undirected, unweighted graph G = (V, E), with diameter denoted as k*. Let Rk(u) represent the set of nodes that are exactly k hops away from node u, where k ∈ [0, k*]. Let s(S) denote the ordered degree sequence of a node set S ⊂ V. Here is an example:
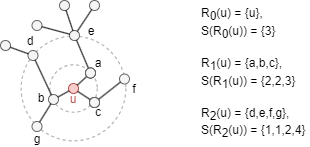
Let fk(u,v) denote the structural distance between nodes u and v, considering their k-hop neighborhoods (all nodes within a distance less than or equal to k):
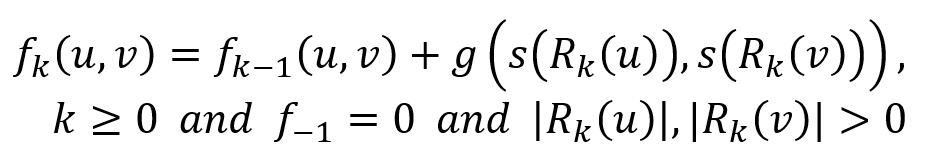
where function g() ≥ 0 measures the distance between two degree sequences. Note that fk(u,v) is non-decreasing in k and is defined only when both u and v have neighbors at distance k.
To measure the distance between the sequences s(Rk(u)) and s(Rk(v)), which may differ in length, Dynamic Time Wrapping (DTW), or any other appliable function, can be adopted. Note that if the k-hop neighborhoods of nodes u and v are isomorphic, then fk-1(u,v) = 0.
2. Construct a multilayer weighted graph
Struc2Vec constructs a multilayer weighted graph M that encodes structural similarity between nodes, where each layer k is defined using the k-hop neighborhoods of the nodes.
Each layer k forms a weighted, undirected complete graph with node set V, containing edges. The edge weight between nodes u and v is inversely proportional to their structural distance, as defined as:
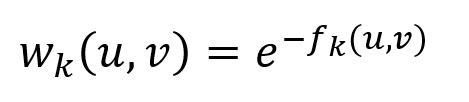
Note that edges are defined only if fk(u,v) is defined.
Layers are connected by directed edges. Every node is connected to its corresponding node in the adjacent layers (if such layers exist). The weights of these inter-layer edges are as follows:
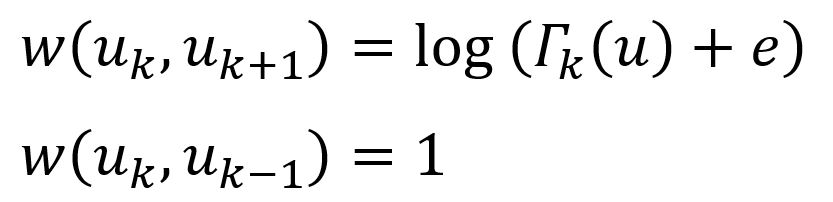
where Γk(u) is the number of edges incident to u that have weight larger than the average edge weight of the complete graph in layer k. Γk(u) actually measures the similarity of node u to other nodes in layer k. Note that if node u has many similar nodes in layer k, then it should change to higher layers to obtain a more refined context.
3. Generate context for nodes
Struc2Vec uses random walks to generate sequence of nodes to determine the context of a gievn node.
Consider a biased random walk that operates on graph M. Each node starts the walk in its corresponding node in layer 0. When the walk reaches node u in layer k (denoted as uk), the random walk first decides if it will (1) stay in the current layer, or (2) change layer:
(1) With probability q, the random walk stays in the current layer: the probability of moving to vk is proportional to wk(u,v). Note that the random walk will prefer to step onto nodes that are structurally more similar to the current node.
(2) With probability 1 − q, the random walk changes layer: the probabilities of moving to uk+1 or uk-1 are proportional to wk(uk,uk+1) and wk(uk,uk-1). It's important to note that in this case, the node u is recorded only once in the random walk sequence.
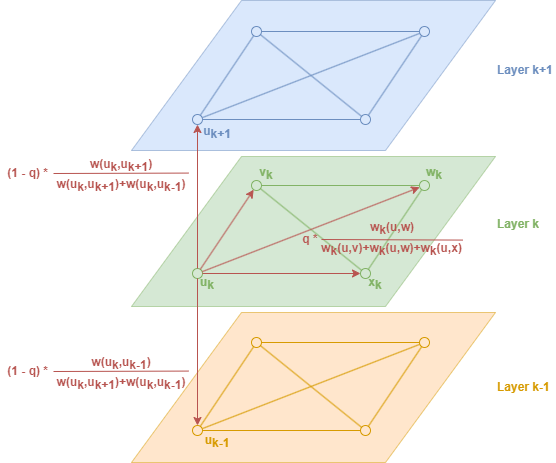
The random walks have a fixed and relatively short depth (number of steps), and the process is repeated a certain number of times.
4. Train the model
The node sequences generated from the random walks serve as input to the Skip-gram model. SGD is used to optimize the model's parameters based on the prediction error, with optimization techniques such as negative sampling and subsampling applied to enhance efficiency.
Considerations
- When calculating the degree of a node, each self-loop is counted twice.
- The Struc2Vec algorithm treats all edges as undirected, ignoring their original direction.
Example Graph
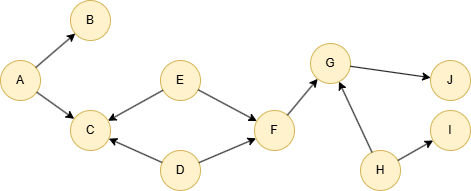
Run the following statements on an empty graph to define its structure and insert data:
INSERT (A:default {_id: "A"}),
(B:default {_id: "B"}),
(C:default {_id: "C"}),
(D:default {_id: "D"}),
(E:default {_id: "E"}),
(F:default {_id: "F"}),
(G:default {_id: "G"}),
(H:default {_id: "H"}),
(I:default {_id: "I"}),
(J:default {_id: "J"}),
(A)-[:default]->(B),
(A)-[:default]->(C),
(D)-[:default]->(C),
(D)-[:default]->(F),
(E)-[:default]->(C),
(E)-[:default]->(F),
(F)-[:default]->(G),
(G)-[:default]->(J),
(H)-[:default]->(G),
(H)-[:default]->(I);
insert().into(@default).nodes([{_id:"A"},{_id:"B"},{_id:"C"},{_id:"D"},{_id:"E"},{_id:"F"},{_id:"G"},{_id:"H"},{_id:"I"},{_id:"J"}]);
insert().into(@default).edges([{_from:"A", _to:"B"}, {_from:"A", _to:"C"}, {_from:"D", _to:"C"}, {_from:"D", _to:"F"}, {_from:"E", _to:"C"}, {_from:"E", _to:"F"}, {_from:"F", _to:"G"}, {_from:"G", _to:"J"}, {_from:"H", _to:"G"}, {_from:"H", _to:"I"}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: struc2vec
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
ids |
[]_id |
/ | / | Yes | Specifies nodes to start random walk by their _id. If unset, computation includes all nodes. |
uuids |
[]_uuid |
/ | / | Yes | Specifies nodes to start random walk by their _uuid. If unset, computation includes all nodes. |
walk_length |
Integer | ≥1 | 1 |
Yes | Depth of each walk, i.e., the number of nodes to visit. |
walk_num |
Integer | ≥1 | 1 |
Yes | Number of walks to perform for each specified node. |
k |
Integer | [1, 10] | / | No | Number of layers in the constructed multilayer weighted graph, which should not exceed the diameter of the original graph. |
stay_probability |
Float | (0,1] | / | No | The probability of walking in the current level. |
window_size |
Integer | ≥1 | / | No | The maximum size of context. |
dimension |
Integer | ≥2 | / | No | Dimensionality of the embeddings. |
loop_num |
Integer | ≥1 | / | No | Number of training iterations. |
learning_rate |
Float | (0,1) | / | No | Learning rate used initially for training the model, which decreases after each training iteration until reaches min_learning_rate. |
min_learning_rate |
Float | (0,learning_rate) |
/ | No | Minimum threshold for the learning rate as it is gradually reduced during the training. |
neg_num |
Integer | ≥1 | 5 |
Yes | Number of negative samples to produce for each positive sample, it is suggested to set between 1 to 10. |
resolution |
Integer | ≥1 | 1 |
Yes | The parameter used to enhance negative sampling efficiency; a higher value offers a better approximation to the original noise distribution; it is suggested to set as 10, 100, etc. |
sub_sample_alpha |
Float | / | 0.001 |
Yes | The factor affecting the probability of down-sampling frequent nodes; a higher value increases this probability; a value ≤0 means not to apply subsampling |
min_frequency |
Integer | / | / | No | Nodes that appear less times than this threshold in the training "corpus" will be excluded from the "vocabulary" and disregarded in the embedding training; a value ≤0 means to keep all nodes. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both values to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned. Set to -1 to include all results. |
File Writeback
CALL algo.struc2vec.write("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}, {
file: {
filename: "embeddings"
}
})
algo(struc2vec).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}).write({
file: {
filename: "embeddings"
}
})
DB Writeback
Writes the embedding_result values from the results to the specified node property. The property type is float[].
CALL algo.struc2vec.write("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}, {
db: {
property: "vector"
}
})
algo(struc2vec).params({
projection: "my_hdc_graph",
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}).write({
db: {
property: "vector"
}
})
Full Return
CALL algo.struc2vec.run("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) YIELD embeddings
RETURN embeddings
exec{
algo(struc2vec).params({
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 4,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) as embeddings
return embeddings
} on my_hdc_graph
Stream Return
CALL algo.struc2vec.stream("my_hdc_graph", {
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) YIELD embeddings
RETURN embeddings
exec{
algo(struc2vec).params({
return_id_uuid: "id",
walk_length: 10,
walk_num: 20,
k: 10,
stay_probability: 0.4,
window_size: 5,
dimension: 5,
loop_number: 10,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 9,
resolution: 100,
sub_sample_alpha: 0.001,
min_frequency: 3
}) as embeddings
return embeddings
} on my_hdc_graph

