Overview
Betweenness centrality measures the likelihood of a node being on the shortest paths between any two other nodes. This metric effectively identifies "bridge" nodes that facilitate connectivity between different parts of a graph.
Betweenness centrality values range from 0 to 1, with higher scores indicating nodes that exert greater influence over the flow and connectivity of the network.
References:
- L.C. Freeman, A Set of Measures of Centrality Based on Betweenness (1977)
- L.C. Freeman, Centrality in Social Networks Conceptual Clarification (1978)
Concepts
Shortest Path
The shortest paths between two nodes are the paths that contain the fewest edges. When considering edge weights, the (weighted) shortest paths are those with the lowest total weight sum.
Betweenness Centrality
The betweenness centrality of a node x is computed by:
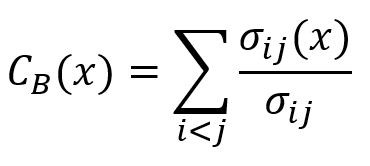
where,
iandjare two distinct nodes in the graph, excludingx.σijis the total number of shortest paths betweeniandj.σij(x)is the number of shortest paths betweeniandjthat pass through nodex.σij(x)/σijgives the probability thatxlies in the shortest paths betweeniandj. Note that ifiandjare not connected,σij(x)/σijis 0.
The final value is normalized by the factor (k – 1)(k – 2)/2, where k is the total number of nodes in the graph. This normalization ensures the result lies within a fixed range, making it comparable across graphs of different sizes.
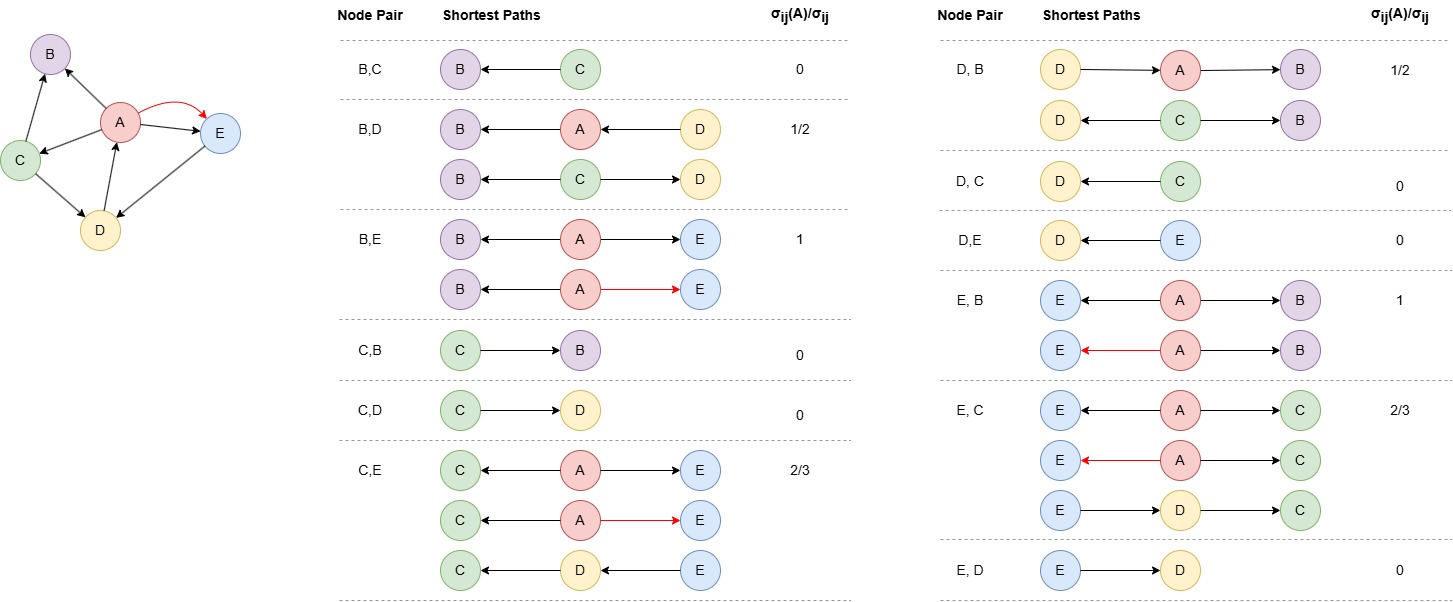
The betweenness centrality of node A is computed as: (1/2 + 1 + 2/3 + 1/2 + 1 + 2/3) / (4 * 3 / 2) = 0.722222.
Sampling
This algorithm requires substantial computational resources when applied to large graphs. When the number of nodes in a graph exceeds 10,000, it is recommended to sample nodes or edges for approximate computation. The algorithm performs a single uniform sampling.
Example Graph
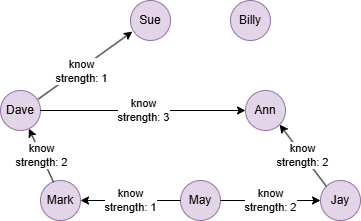
Run the following statements on an empty graph to define its structure and insert data:
ALTER GRAPH CURRENT_GRAPH ADD NODE {
user ()
};
ALTER GRAPH CURRENT_GRAPH ADD EDGE {
know ()-[{strength int32}]->()
};
INSERT (Sue:user {_id: "Sue"}),
(Dave:user {_id: "Dave"}),
(Ann:user {_id: "Ann"}),
(Mark:user {_id: "Mark"}),
(May:user {_id: "May"}),
(Jay:user {_id: "Jay"}),
(Billy:user {_id: "Billy"}),
(Dave)-[:know {strength: 1}]->(Sue),
(Dave)-[:know {strength: 3}]->(Ann),
(Mark)-[:know {strength: 2}]->(Dave),
(May)-[:know {strength: 1}]->(Mark),
(May)-[:know {strength: 2}]->(Jay),
(Jay)-[:know {strength: 2}]->(Ann);
create().node_schema("user").edge_schema("know");
create().edge_property(@know, "strength", int32);
insert().into(@user).nodes([{_id:"Sue"}, {_id:"Dave"}, {_id:"Ann"}, {_id:"Mark"}, {_id:"May"}, {_id:"Jay"}, {_id:"Billy"}]);
insert().into(@know).edges([{_from:"Dave", _to:"Sue", strength:1}, {_from:"Dave", _to:"Ann", strength:3}, {_from:"Mark", _to:"Dave", strength:2}, {_from:"May", _to:"Mark", strength:1}, {_from:"May", _to:"Jay", strength:2}, {_from:"Jay", _to:"Ann", strength:2}]);
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as my_hdc_graph:
CREATE HDC GRAPH my_hdc_graph ON "hdc-server-1" OPTIONS {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}
hdc.graph.create("my_hdc_graph", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static"
}).to("hdc-server-1")
Parameters
Algorithm name: betweenness_centrality
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
edge_schema_property |
[]"<@schema.?><property>" |
/ | / | Yes | Numeric edge properties used as weights, summing values across the specified properties; edges without this property are ignored. |
impl_type |
String | dijkstra, spfa |
dijkstra |
Yes | Specifies the weighted shortest paths to be computed by the Dijkstra or SPFA shortest path algorithm. This is only valid when edge_schema_property is used. |
sample_size |
Integer | -1, -2, [1, |V|] |
-2 |
Yes | Sets to -1 to sample log10(|V|) nodes (|V| is total number of nodes in the graph), or sets a custom number between [1, |V|]; sets to -2 to perform no sampling. |
max_path_length |
Integer | >0 | / | Yes | Limits the shortest paths considered to those with a length no greater than this value. Note that this doesn't affect the total number of node pairs evaluated. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results. |
limit |
Integer | ≥-1 | -1 |
Yes | Limits the number of results returned; -1 includes all results. |
order |
String | asc, desc |
/ | Yes | Sorts the results by betweenness_centrality. |
File Writeback
CALL algo.betweenness_centrality.write("my_hdc_graph", {
return_id_uuid: "id"
}, {
file: {
filename: "betweenness_centrality"
}
})
algo(betweenness_centrality).params({
projection: "my_hdc_graph",
return_id_uuid: "id"
}).write({
file: {
filename: "betweenness_centrality"
}
})
Result:
_id,betweenness_centrality
Dave,0.666667
Billy,0
May,0.133333
Mark,0.266667
Jay,0.133333
Ann,0.266667
Sue,0
DB Writeback
Writes the betweenness_centrality values from the results to the specified node property. The property type is float.
CALL algo.betweenness_centrality.write("my_hdc_graph", {},
{
db: {
property: "bc"
}
})
algo(betweenness_centrality).params({
projection: "my_hdc_graph"
}).write({
db:{
property: 'bc'
}
})
Full Return
CALL algo.betweenness_centrality.run("my_hdc_graph", {
max_path_length: 2,
return_id_uuid: "id",
order: "desc",
limit: 3
}) YIELD bc
RETURN bc
exec{
algo(betweenness_centrality).params({
max_path_length: 2,
return_id_uuid: "id",
order: "desc",
limit: 3
}) as bc
return bc
} on my_hdc_graph
Result:
| _id | betweenness_centrality |
|---|---|
| Dave | 0.4 |
| May | 0.133333 |
| Mark | 0.133333 |
Stream Return
CALL algo.betweenness_centrality.stream("my_hdc_graph", {
return_id_uuid: "id",
edge_schema_property: "strength"
}) YIELD r
FILTER r.betweenness_centrality > 0.6
RETURN r
exec{
algo(betweenness_centrality).params({
return_id_uuid: "id",
edge_schema_property: "strength"
}).stream() as r
where r.betweenness_centrality > 0.6
return r
} on my_hdc_graph
Result:
| _id | betweenness_centrality |
|---|---|
| Dave | 0.6 |

