Overview
The k-Core algorithm identifies the maximal connected subgraph where all nodes have a minimum degree of k. It is commonly employed to extract closely connected groups in a graph for further analysis. The algorithm is widely utilized in various research domains including financial risk control, social network analysis, and biology. One of the key advantages of the k-Core algorithm is its low time complexity (linear), making it efficient for large-scale graph processing. Additionally, the resulting subgraphs have good intuitive interpretability, aiding in the understanding of the graph's structural patterns and relationships.
The commonly accepted concept of k-core was first proposed by Seidman:
- S.B. Seidman, Network Structure And Minimum Degree. Soc Netw 5:269-287 (1983)
Concepts
k-Core
The k-core of a graph is obtained through an iterative pruning process. Starting with the original graph, nodes with a degree less than k are successively removed until only nodes with degrees greater than or equal to k remain.
Below is the pruning process to get the 3-core of the graph. In the first round, nodes {a, d, f} with degree less than 3 are removed , which then affects the removal of node b in the second round. After the second round, all remaining nodes have a degree of at least 3. Therefore, the pruning process ends, and the 3-core of this graph is induced by nodes {c, e, g, h}.

Ultipa's k-Core algorithm identifies the k-core in each connected component.
Considerations
- The k-Core algorithm ignores self-loops in the graph. Any self-loop present is not considered when calculating the degree of the respective node.
- The k-Core algorithm ignores the direction of edges but calculates them as undirected edges.
Example Graph
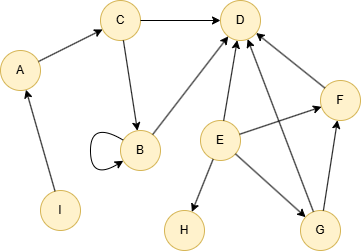
To create this graph:
// Runs each row separately in order in an empty graphset
insert().into(@default).nodes([{_id:"A"}, {_id:"B"}, {_id:"C"}, {_id:"D"}, {_id:"E"}, {_id:"F"}, {_id:"G"}, {_id:"H"}, {_id:"I"}])
insert().into(@default).edges([{_from:"A", _to:"C"}, {_from:"B", _to:"B"}, {_from:"B", _to:"D"}, {_from:"C", _to:"B"}, {_from:"C", _to:"D"}, {_from:"E", _to:"D"}, {_from:"E", _to:"F"}, {_from:"E", _to:"G"}, {_from:"E", _to:"H"}, {_from:"F", _to:"D"}, {_from:"G", _to:"D"}, {_from:"G", _to:"F"}, {_from:"I", _to:"A"}])
Running on HDC Graphs
Creating HDC Graph
To load the entire graph to the HDC server hdc-server-1 as hdc_kcore:
CALL hdc.graph.create("hdc-server-1", "hdc_kcore", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
})
hdc.graph.create("hdc_kcore", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true,
update: "static",
query: "query",
default: false
}).to("hdc-server-1")
Parameters
Algorithm name: k_core
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
k |
Integer | ≥1 | / | No | Specifies the minimum degree k for nodes to be included in the k-core subgraph. |
return_id_uuid |
String | uuid, id, both |
uuid |
Yes | Includes _uuid, _id, or both to represent nodes in the results; this option is only valid in File Writeback. |
File Writeback
CALL algo.k_core.write("hdc_kcore", {
params: {
k: 3,
return_id_uuid: "id"
},
return_params: {
file: {
filename: "3-core.txt"
}
}
})
algo(k_core).params({
projection: "hdc_kcore",
k: 3,
return_id_uuid: "id"
}).write({
file: {
filename: "3-core.txt"
}
})
Result:
_id
G
F
E
D
Full Return
CALL algo.k_core("hdc_kcore", {
params: {
k: 2
},
return_params: {}
}) YIELD k2
RETURN k2
exec{
algo(k_core).params({
k: 2
}) as result
return result
} on hdc_kcore
[{"id":"G","uuid":"13690943966717935617","schema":"default","values":{}}]
[{"id":"D","uuid":"288231475663339522","schema":"default","values":{}}]
[{"id":"F","uuid":"2882304861028745219","schema":"default","values":{}}]
[{"id":"B","uuid":"3530823207370096641","schema":"default","values":{}}]
[{"id":"E","uuid":"10520409829049106435","schema":"default","values":{}}]
[{"id":"C","uuid":"12033619303845593090","schema":"default","values":{}}]
Stream Return
CALL algo.k_core("hdc_kcore", {
params: {
k: 3
},
return_params: {
stream: {}
}
}) YIELD r
FOR node in r
RETURN node._id
exec{
algo(k_core).params({
k: 3
}).stream() as r
uncollect r as node
return node._id
} on hdc_kcore
Result:
| node._id |
|---|
| G |
| D |
| F |
| E |
Running on Distributed Projections
Creating Distributed Projection
To project the entire graph to its shard servers as dist_kcore:
create().projection("dist_kcore", {
nodes: {"*": ["*"]},
edges: {"*": ["*"]},
direction: "undirected",
load_id: true
})
Parameters
Algorithm name: k_core
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
k |
Integer | ≥1 | / | No | Specifies the minimum degree k for nodes to be included in the k-core subgraph. |
File Writeback
CALL algo.k_core.write("dist_kcore", {
params: {
k: 3
},
return_params: {
file: {
filename: "3-core.txt"
}
}
})
algo(k_core).params({
projection: "dist_kcore",
k: 3
}).write({
file: {
filename: "3-core.txt"
}
})
_id
E
D
F
G

