Overview

The Bipartite algorithm is used to determine whether a given graph is a bipartite graph. By applying the algorithm, it becomes possible to identify and utilize the inherent structure of bipartite graphs in different scenarios, enabling efficient resource allocation, task assignment, and grouping optimization.

The Bipartite algorithm returns 1 if the graph is bipartite and 0 otherwise.

Concepts

Bipartite Graph

A bipartite graph, also known as a bigragh, is a graph which the nodes can be divided into two disjoint sets, such that every edge in the graph connects a node from one set to a node from the other set. In other words, there are no edges that connect nodes within the same set.

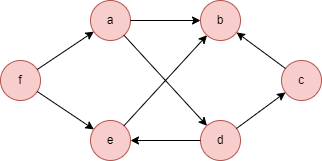
This example graph is bipartite. The nodes can be partitioned into sets V₁ = {A, D, E} and V₂ = {B, C, F}.

Coloring Method

To determine if a graph is bipartite, one common approach is to perform a graph traversal and assign each visited node to one of two different sets. This process is often referred to as "coloring" the nodes. During the traversal, if an edge is encountered that connects two nodes within the same set, then the graph is not bipartite. Conversely, if all edges connect nodes from different sets, the graph is bipartite.

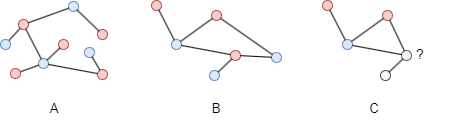
In this example, both graph A and graph B are bipartite. Graph C is not bipartite as it contains an odd cycle. An odd cycle is a cycle that has an odd number of nodes. Bipartite graphs cannot contain odd cycles because it is not possible to color all the nodes of an odd cycle using only two colors while still meeting the requirement of bipartiteness. This property, where bipartite graphs never contain any odd cycles, is a fundamental characteristic of bipartite graphs.

Considerations

• Two endpoints of a self-loop are the same node, thus graphs that have any self-loop are not bipartite.
• The Bipartite algorithm ignores the direction of edges but calculates them as undirected edges.

Example Graph

To create this graph:

// Runs each row separately in order in an empty graphset
insert().into(@default).nodes([{_id:"a"}, {_id:"b"}, {_id:"c"}, {_id:"d"}, {_id:"e"}, {_id:"f"}])
insert().into(@default).edges([{_from:"a", _to:"b"}, {_from:"a", _to:"d"}, {_from:"c", _to:"b"}, {_from:"d", _to:"c"}, {_from:"d", _to:"e"}, {_from:"e", _to:"b"}, {_from:"f", _to:"a"}, {_from:"f", _to:"e"}])

Creating HDC Graph

To load the entire graph to the HDC server hdc-server-1 as hdc_bipartite:

CALL hdc.graph.create("hdc-server-1", "hdc_bipartite", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
})

hdc.graph.create("hdc_bipartite", {
  nodes: {"*": ["*"]},
  edges: {"*": ["*"]},
  direction: "undirected",
  load_id: true,
  update: "static",
  query: "query",
  default: false
}).to("hdc-server-1")

Parameters

Algorithm name: bipartite

The algorithm does not require any parameters.

Full Return

CALL algo.bipartite("hdc_bipartite", {params: {}}) YIELD r
RETURN r

exec{
  algo(bipartite).params() as r
  return r
} on hdc_bipartite

Result:

Stream Return

CALL algo.bipartite("hdc_bipartite", {
  params: {},
  return_params: {
  	stream: {}
  }
}) YIELD result
RETURN result

exec{
  algo(bipartite).params().stream() as result
  return result
} on hdc_bipartite

Result:

Stats Return

CALL algo.bipartite("hdc_bipartite", {
  params: {},
  return_params: {
  	stats: {}
  }
}) YIELD result
RETURN result

exec{
  algo(bipartite).params().stats() as result
  return result
} on hdc_bipartite

Result: