Overview
Closeness centrality of a node is measured by the average shortest distance from the node to all other reachable nodes. The closer a node is to all other nodes, the more central the node is. This algorithm is widely used in applications such as discovering key social nodes and finding best locations for functional places.
Closeness Centrality algorithm is best to be applied in connected graph. For disconnected graph, its variant, the Harmonic Centrality, is recommended.
Closeness centrality takes on values between 0 to 1, nodes with higher scores have shorter distances to all other nodes.
Closeness centrality was originally defined by Alex Bavelas in 1950:
- A. Bavelas, Communication patterns in task-oriented groups (1950)
Concepts
Shortest Distance
The shortest distance of two nodes is the number of edges contained in the shortest path between them. Shortest path is searched by the BFS principle, if node A is regarded as the start node and node B is one of the K-hop neighbors of node A, then K is the shortest distance between A and B. Please read K-Hop All for the details about BFS and K-hop neighbor.
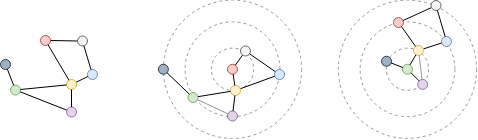
Examine the shortest distance between the red and green nodes in the above graph. Since the graph is undirected, no matter which node (red or green) to start, the other node is the 2-hop neighbor. Thus, the shortest distance between them is 2.
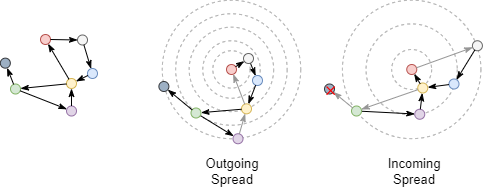
Examine the shortest distance between the red and green nodes after converting the undirected graph to directed graph, the edge direction should be considered now. Outgoing shortest distance from the red node to the green node is 4, incoming shortest distance from the green node to the red node is 3.
Closeness Centrality
Closeness centrality score of a node defined by this algorithm is the inverse of the arithmetic mean of the shortest distances from the node to all other reachable nodes. The formula is:
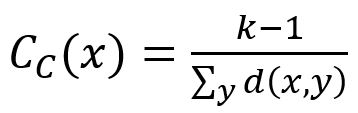
where x is the target node, y is any node that connects with x along edges (x itself is excluded), k-1 is the number of y, d(x,y) is the shortest distance between x and y.
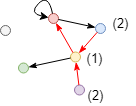
Calculate closeness centrality score of the red node in the incoming direction in the graph above. Only the blue, yellow and purple three nodes can reach the red node in this direction, so the score is 3 / (2 + 1 + 2) = 0.6. Since the green and grey nodes cannot reach the red node in the incoming direction, they are not included in the calculation.
Closeness Centrality algorithm consumes considerable computing resources. For a graph with V nodes, it is recommended to perform (uniform) sampling when V > 10,000, and the suggested number of samples is the base-10 logarithm of the number of nodes (
log(V)).
For each execution of the algorithm, sampling is performed only once, centrality score of each node is computed based on the shortest distance between the node and all sample nodes.
Considerations
- The closeness centrality score of isolated nodes is 0.
- When computing closeness centrality for a node, the unreachable nodes are excluded. For example, isolated nodes, nodes in other connected components, or nodes in the same connected component although cannot access in the specified direction, etc.
Syntax
- Command:
algo(closeness_centrality) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Yes | ID/UUID of the nodes to calculate, calculate for all nodes if not set |
| direction | string | in, out |
/ | Yes | Direction of all edges in each shortest path, in for incoming direction, out for outgoing direction |
| sample_size | int | -1, -2, [1, V] |
-2 |
Yes | Number of samples to compute centrality scores; -1 means to sample log(V) nodes; -2 means not to perform sampling; a number within [1, V] means to sample the set number of nodes; sample_size is only valid when ids (uuids) is ignored or when it specifies all nodes |
| limit | int | ≥-1 | -1 |
Yes | Number of results to return, -1 to return all results |
| order | string | asc, desc |
/ | Yes | Sort nodes by the centrality score |
Examples
The example graph is as follows:
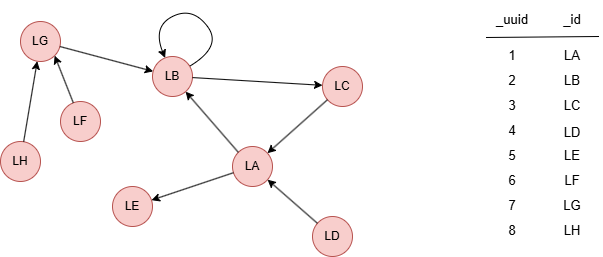
File Writeback
| Spec | Content |
|---|---|
| filename | _id,centrality |
algo(closeness_centrality).params().write({
file:{
filename: 'centrality'
}
})
Results: File centrality
LA,0.583333
LB,0.636364
LC,0.5
LD,0.388889
LE,0.388889
LF,0.368421
LG,0.538462
LH,0.368421
Property Writeback
| Spec | Content | Write to | Data Type |
|---|---|---|---|
| property | centrality |
Node property | float |
algo(closeness_centrality).params().write({
db:{
property: 'cc'
}
})
Results: Centrality score for each node is written to a new property named cc
Direct Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perNode | Node and its centrality | _uuid, centrality |
algo(closeness_centrality).params({
direction: 'out',
order: 'desc',
limit: 3
}) as cc
return cc
Results: cc
| _uuid | centrality |
|---|---|
| 1 | 0.75000000 |
| 3 | 0.60000002 |
| 2 | 0.50000000 |
Stream Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perNode | Node and its centrality | _uuid, centrality |
algo(closeness_centrality).params({
direction: 'in'
}).stream() as cc
where cc.centrality == 0
return cc
Results: cc
| _uuid | centrality |
|---|---|
| 4 | 0.0000000 |
| 6 | 0.0000000 |

