Overview
The Local Clustering Coefficient algorithm calculates the density of connection among the immediate neighbors of a node. It quantifies the ratio of actual connections among the neighbors to the maximum possible connections.
The local clustering coefficient provides insights into the cohesion of a node's ego network. In the context of a social network, the local clustering coefficient helps understand the degree of interconnectedness among an individual's friends or acquaintances. A high local clustering coefficient suggests that the person's friends are likely to be connected to each other, indicating the presence of a closely-knit social group, such as a family. Conversely, a low local clustering coefficient indicates a more dispersed or loosely interconnected ego network, where the person's friends do not have strong connections with each other.
Concepts
Local Clustering Coefficient
Mathematically, the local clustering coefficient of a node in an undirected graph is calculated as the ratio of the number of connected neighbor pairs to the total number of possible neighbor pairs:
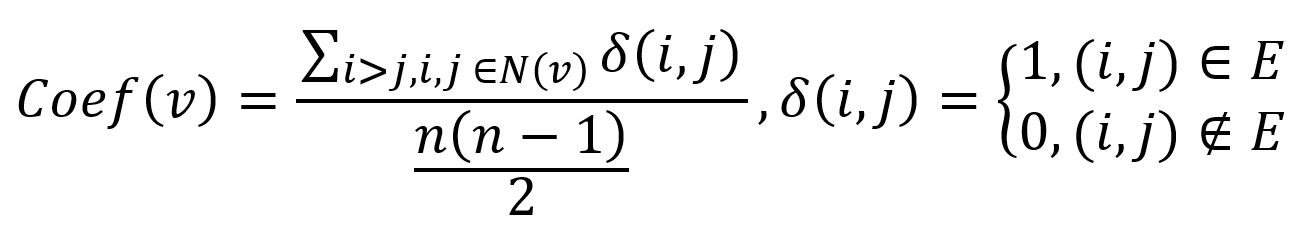
where n is the number of nodes contained in the 1-hop neighborhood of node v (denoted as N(v)), i and j are any two distinct nodes within N(v), δ(i,j) is equal to 1 if i and j are connected, and 0 otherwise.
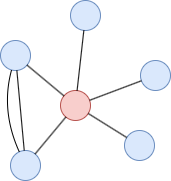
In this example, the local clustering coefficient of the red node is 1/(5*4/2) = 0.1.
Considerations
- The Local Clustering Coefficient algorithm ignores the direction of edges but calculates them as undirected edges.
Syntax
- Command:
algo(clustering_coefficient) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Yes | ID/UUID of nodes to calculate the local clustering coefficient, calculate for all nodes if not set |
| limit | int | ≥-1 | -1 |
Yes | Number of results to return, -1 to return all results |
| order | string | asc, desc |
/ | Yes | Sort nodes by the value of the local clustering coefficient |
Examples
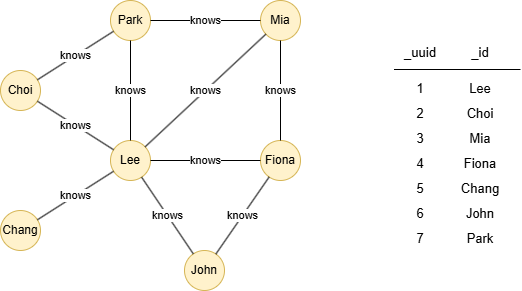
The example graph is as follows:
File Writeback
| Spec | Content |
|---|---|
| filename | _id,centrality |
algo(clustering_coefficient).params({
ids: ['Lee', 'Choi']
}).write({
file:{
filename: 'lcc'
}
})
Results: File lcc
Lee,0.266667
Choi,1
Property Writeback
| Spec | Content | Write to | Data Type |
|---|---|---|---|
| property | centrality |
Node property | float |
algo(clustering_coefficient).params().write({
db:{
property: 'lcc'
}
})
Results: The value of the local clustering coefficient for each node is written to a new property named lcc
Direct Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | []perNode | Node and its local clustering coefficient | _uuid, centrality |
algo(clustering_coefficient).params({
order: 'desc'
}) as lcc
return lcc
Results: lcc
| _uuid | centrality |
|---|---|
| 2 | 1 |
| 6 | 1 |
| 3 | 0.666667 |
| 4 | 0.666667 |
| 7 | 0.666667 |
| 1 | 0.266667 |
| 5 | 0 |
Stream Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | []perNode | Node and its local clustering coefficient | _uuid, centrality |
algo(clustering_coefficient).params().stream() as lcc
where lcc.centrality == 1
return count(lcc)
Results: 2

