Overview
The Leiden algorithm is a community detection algorithm designed to maximize modularity in a graph. It was developed to address potential issues in the results obtained by the popular Louvain algorithm, where some communities may not be well-connected or even disconnected. The Leiden algorithm is faster compared to the Louvain algorithm and guarantees to produce partitions in which all communities are internally connected. The algorithm is also named after the location of its authors.
- V.A. Traag, L. Waltman, N.J. van Eck, From Louvain to Leiden: guaranteeing well-connected communities (2019)
- V.A. Traag, P. Van Dooren, Y. Nesterov, Narrow scope for resolution-limit-free community detection (2011)
Concepts
Modularity
The concept of modularity is explained in the Louvain algorithm. The modularity formula used in the Leiden algorithm is extended to handle different levels of community granularity:
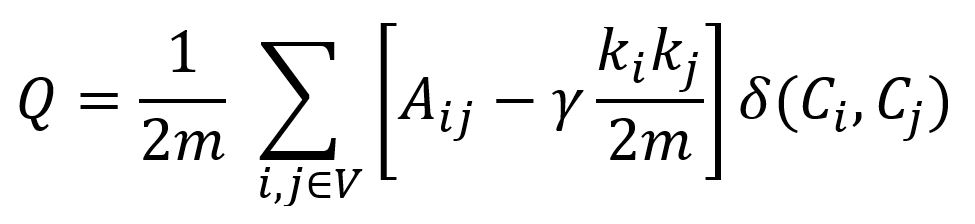
γ > 0 is the resolution parameter that modulates the density of connections within communities and between communities. When γ > 1, it leads to more, smaller and well-connected communities; when γ < 1, it leads to fewer, larger and less well-connected communities.
Leiden
The Leiden algorithm starts from a singleton partition, in which each node is in its own community. Then algorithm iteratively runs through passes, and each pass is made of three phases:
First Phase: Fast Modularity Optimization
Unlike the first phase of the Louvain algorithm, which keeps visiting all nodes in the graph until no node movements can increase the modularity; the Leiden algorithm takes a more efficient approach, it only visits all nodes once, afterwards it visits only nodes whose neighborhood has changed. To do that, the Leiden algorithm maintains a queue and initializes it by adding all nodes in the graph in a random order.
Then repeat the following steps until the queue is empty:
- Remove the first node from the front of the queue.
- Reassign the node to a different community which has the maximum gain of modularity (ΔQ); or keep the node in its original community if there is no positive gain.
- If the node is moved to a different community, add to the rear of the queue all neighbors of the node that do not belong to the node’s new community and that are not yet in the queue.
The first phase ends with a partition P of the base or aggregate graph.
Second Phase: Refinement
This phase is designed to get a refined partition Prefined of P to guarantee that all communities are well-connected.
Prefined is initially set to a singleton partition, in which each node in the base or aggregate graph is in its own community. Refine each community C ∈ P as follows.
1. Consider only nodes v ∈ C that are well-connected within C:
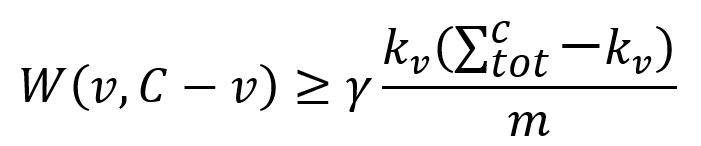
where,
- W(v,C-v) is the sum of edge weights between node v and the rest of nodes in C;
- kv is the sum of weights of all edges attached to node v;
- the sum of weights of all edges attached to nodes in C.
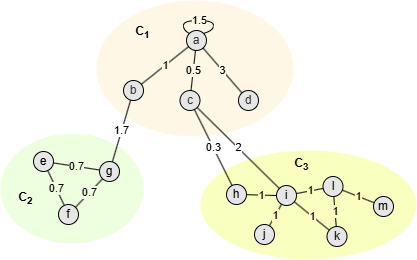
Take community C1 in the above graph as example, where
- m = 18.1
- = ka + kb + kc + kd = 6 + 2.7 + 2.8 + 3 = 14.5
Set γ as 1.2, then:
- W(a, C1) - γ/m ⋅ ka ⋅ (
∑ tot C 1 - W(b, C1) - γ/m ⋅ kb ⋅ (
∑ tot C 1 - W(c, C1) - γ/m ⋅ kc ⋅ (
∑ tot C 1 - W(d, C1) - γ/m ⋅ kd ⋅ (
∑ tot C 1
In this case, only nodes a and d are considered well-connected in community C1.
2. Visit each node v in random order, if it is still on its own in a community in Prefined, randomly merge it to a community C' ∈ Prefined for which the modularity increases. It is required that C' must be well-connected with C:
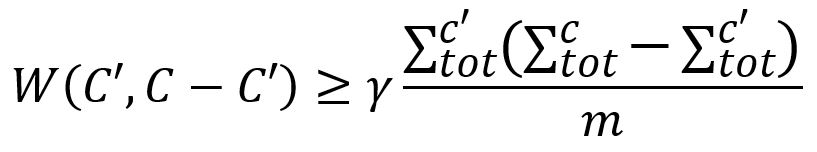
Note that in this phase, each node is not necessarily greedily merged with the community that yields the maximum gain of modularity. However, the larger the gain, the more likely a community is to be selected. The degree of randomness in the selection of a community is determined by a parameter θ > 0:
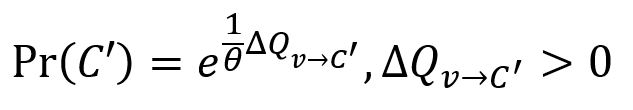
Randomness in the selection of a community allows the partition space to be explored more broadly.
After the refinement phase is concluded, communities in P often are split into multiple communities in Prefined, but not always.
Third Phase: Community Aggregation
The aggregate graph is created based on Prefined. However, the partition for the aggregate graph is based on P. The aggregation process is the same as Louvain.
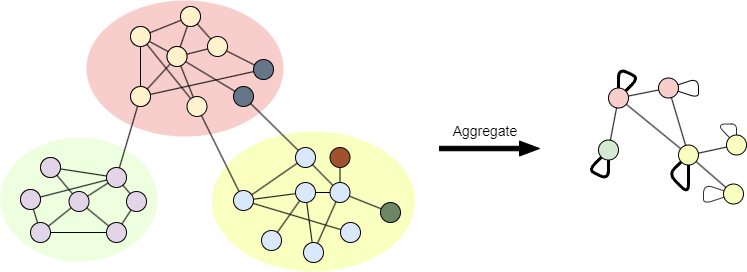
Once this third phase is completed, another pass is applied to the aggregate graph. The passes are iterated until there are no more changes, and a maximum modularity is attained.
Considerations
- If node i has any self-loop, when calculating ki, the weight of self-loop is counted only once.
- The Leiden algorithm ignores the direction of edges but calculates them as undirected edges.
Syntax
- Command:
algo(leiden) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| phase1_loop_num | int | ≥1 | 5 |
Yes | The maximum loop number of the first phase during each pass |
| min_modularity_increase | float | [0,1] | 0.01 |
Yes | The minimum gain of modularity (ΔQ) to move a node to another community in the first phase |
| edge_schema_property | []@<schema>?.<property> |
Numeric type, must LTE | / | Yes | Edge properties to use as weights, where the values of multiple properties are summed up; all edge weights are considered as 1 if not set |
| gamma | float | >0 | 1 | Yes | The resolution parameter γ |
| theta | float | >0 | 0.01 | Yes | The parameter θ which controls the degree of randomness during community merging in the second phase |
| limit | int | ≥-1 | -1 |
Yes | Number of results to return, -1 to return all results |
| order | string | asc, desc |
/ | Yes | Sort communities by the number of nodes in it (only valid in mode 2 of the stream() execution) |
Examples
File Writeback
| Spec | Content | Description |
|---|---|---|
| filename_community_id | _id,community_id |
Node and its community ID |
| filename_ids | community_id,_id,_id,... |
Community ID and the ID of nodes in it |
| filename_num | community_id,count |
Community ID and the number of nodes in it |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
file:{
filename_community_id: 'communityID',
filename_ids: 'ids',
filename_num: 'num'
}
})
Property Writeback
| Spec | Content | Write to | Data Type |
|---|---|---|---|
| property | community_id |
Node property | uint32 |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
db:{
property: 'communityID'
}
})
Direct Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | []perNode | Node and its community ID | _uuid, community_id |
| 1 | KV | Number of communities, modularity | community_count, modularity |
algo(leiden).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}) as results, stats
return results, stats
Stream Return
| Spec | Content | Alias Ordinal | Type | Description | Columns |
|---|---|---|---|---|---|
| mode | 1 or if not set |
0 | []perNode | Node and its community ID | _uuid, community_id |
2 |
[]perCommunity | Community and the number of nodes in it | community_id, count |
algo(leiden).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}).stream() as results
group by results.community_id
return table(results.community_id, max(results._uuid))
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
order: "desc"
}).stream({
mode: 2
}) as results
return results
Stats Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | KV | Number of communities, modularity | community_count, modularity |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1
}).stats() as stats
return stats

