Overview
The single-source shortest path (SSSP) problem is that of computing, for each node that is reachable from the source node, the shortest path with the minimum total edge weights among all possible paths; or in the case of unweighted graphs, the shortest path with the minimum number of edges. The cost (or distance) of the shortest path is the total edge weights or the number of edges.
The Delta-Stepping algorithm can be viewed as a variant of Dijkstra's algorithm with its potential for parallelism.
Related material of the algorithm:
- U. Meyer, P.Sanders, Δ-Stepping: A Parallel Single Source Shortest Path Algorithm (1998)
Concepts
Delta-Stepping Single-Source Shortest Path
The Delta-Stepping Single-Source Shortest Path (SSSP) algorithm introduces the concept of "buckets" and performs relaxation operations in a more coarse-grained manner. The algorithm utilizes a positive real number parameter delta (Δ) to achieve the following:
- Maintain an array B of buckets such that B[i] contains nodes whose distance falls within the range [iΔ, (i+1)Δ). Thus Δ is also called the "step width" or "bucket width".
- Distinguish between light edges with weight ≤ Δ and heavy edges with weight > Δ in the graph. Light-edge nodes are prioritized during relaxation as they have lower weights and are more likely to yield shorter paths.
The term relaxation refers to the process of updating the distance of a node v that is connected to node u to a potential shorter distance by considering the path through node u. Specifically, the distance of node v is updated to dist(v) = dist(u) + w(u,v), where w(u,v) is the weight of the edge (u,v). This update is performed only if the current dist(v) is greater than dist(u) + w(u,v).
In the Delta-Stepping SSSP algorithm, the relaxation also includes assigning the relaxed node to the corresponding bucket based on its updated distance value.
Below is the description of the basic Delta-Stepping SSSP algorithm, along with an example to compute the weighted shortest paths in an undirected graph starting from the source node b, and Δ is set to 3:
1. At the begining of the algorithm, all nodes have the distance as infinity except for the source node as 0. The source node is assigned to bucket B[0].

2. In each iteration, remove all nodes from the first nonempty bucket B[i]:
- Relax all light-edge neighbors of the removed nodes, the relaxed nodes might be assigned to B[i] or B[i+1]; defer the relaxation of the heavy-edge neighbors.
- If B[i] is refilled, repeat the above operation until B[i] is empty.
- Relax all deferred heavy-edge neighbors.

Relax light-edge neighbors a with dist(a) = min(0+2,∞) = 2, and d with dist(b) = min(0+3,∞) = 3.

Light-edge neighbor b cannot be relaxed.
Relax heavy-edge neighbor c with dist(c) = min(0+5,∞) = 5, d cannot be relaxed.
3. Repeat step 2 until all buckets are empty.
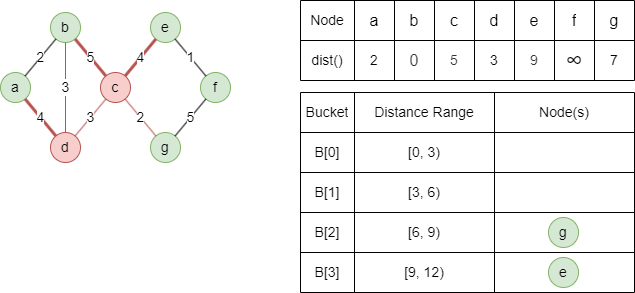
Relax light-edge neighbor g with dist(g) = min(5+2,∞) = 7, b, c and d cannot be relaxed.
Relax heavy-edge neighbor e with dist(e) = min(5+4,∞) = 9, a and b cannot be relaxed.

Light-edge neighbor c cannot be relaxed.
Relax heavy-edge neighbor f with dist(f) = min(7+5,∞) = 12.
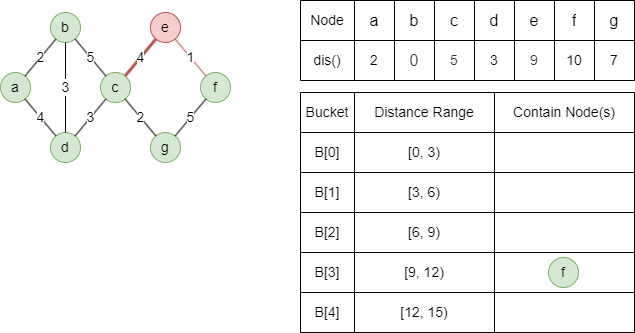
Relax light-edge neighbor f with dist(f) = min(9+1,12) = 10.
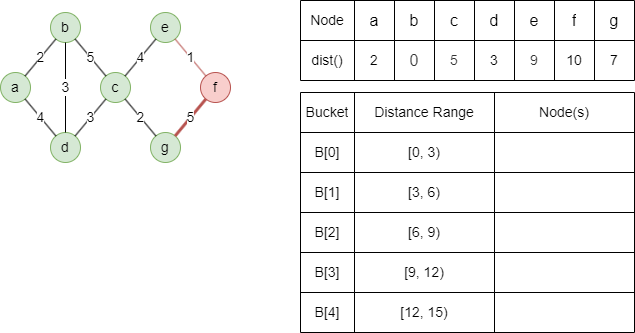
Light-edge neighbor e cannot be relaxed.
Heavy-edge neighbor g cannot be relaxed.
The algorithm ends here since all buckets are empty.
By dividing the nodes into buckets and processing them in parallel, the Delta-Stepping algorithm can exploit the available computational resources more efficiently, making it suitable for large-scale graphs and parallel computing environments.
Considerations
- The Delta-Stepping SSSP algorithm is only applicable to graphs with non-negative edge weights. If negative weights are present, the Delta-Stepping SSSP algorithm might produce false results. In this case, a different algorithm like the SPFA should be used.
- If there are multiple shortest paths exist between two nodes, all of them will be found.
- In disconnected graphs, the algorithm only outputs the shortest paths from the source node to all nodes belonging to the same connected component as the source node.
Syntax
- Command:
algo(sssp) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| ids / uuids | _id / _uuid |
/ | / | No | ID/UUID of the single source node |
| direction | string | in, out |
/ | Yes | Direction of the shortest path, ignore the edge direction if not set |
| edge_schema_property | []@schema?.property |
Numeric type, must LTE | / | Yes | One or multiple edge properties to be used as edge weights, where the values of multiple properties are summed up; treat the graph as unweighted if not set |
| record_path | int | 0, 1 |
0 |
Yes | 1 to return the shortest paths, 0 to return the shortest distances |
| sssp_type | string | delta_stepping |
dijkstra |
No | To run the Delta-Stepping SSSP algorithm, keep it as delta_stepping |
| delta | float | >0 | 2 |
Yes | The value of delta |
| limit | int | ≥-1 | -1 |
Yes | Number of results to return, -1 to return all results |
| order | string | asc, desc |
/ | Yes | Sort nodes by the shortest distance from the source node |
Examples
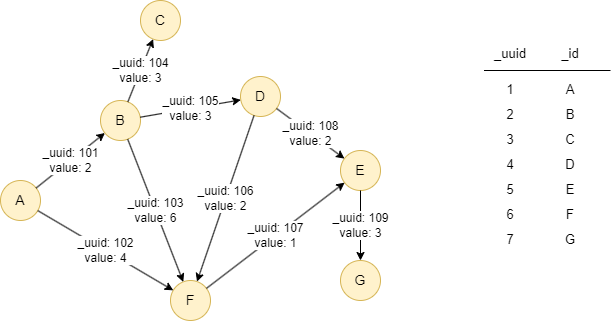
The example graph is as follows:
File Writeback
| Spec | record_path |
Content | Description |
|---|---|---|---|
| filename | 0 | _id,totalCost |
The shortest distance/cost from the source node to each other node |
| 1 | _id--_uuid--_id |
The shortest path from the source node to each other node, the path is represented by the alternating ID of nodes and UUID of edges that form the path |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2
}).write({
file: {
filename: 'costs'
}
})
Results: File costs
G,8
F,4
E,5
D,5
C,5
B,2
A,0
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2,
record_path: 1
}).write({
file: {
filename: 'paths'
}
})
Results: File paths
A--[102]--F--[107]--E--[109]--G
A--[102]--F--[107]--E
A--[101]--B--[105]--D
A--[101]--B--[104]--C
A--[102]--F
A--[101]--B
A
Direct Return
| Alias Ordinal | record_path |
Type | Description | Columns |
|---|---|---|---|---|
| 0 | 0 | []perNode | The shortest cost/distance from the source node to each other node | _uuid, totalCost |
| 1 | []perPath | The shortest path from the source node to each other node, the path is represented by the alternating UUID of nodes and UUID of edges that form the path | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
delta: 2,
order: 'desc'
}) as costs
return costs
Results: costs
| _uuid | totalCost |
|---|---|
| 7 | 8 |
| 5 | 5 |
| 4 | 5 |
| 3 | 5 |
| 6 | 4 |
| 2 | 2 |
| 1 | 0 |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
direction: 'out',
record_path: 1,
sssp_type: 'delta_stepping',
delta: 2,
order: 'asc'
}) as paths
return paths
Results: paths
| 1 |
| 1--[101]--2 |
| 1--[102]--6 |
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6--[107]--5--[109]--7 |
Stream Return
| Alias Ordinal | record_path |
Type | Description | Columns |
|---|---|---|---|---|
| 0 | 0 | []perNode | The shortest cost/distance from the source node to each other node | _uuid, totalCost |
| 1 | []perPath | The shortest path from the source node to each other node, the path is represented by the alternating UUID of nodes and UUID of edges that form the path | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping'
}).stream() as costs
where costs.totalCost <> [0,5]
return costs
Results: costs
| _uuid | totalCost |
|---|---|
| 6 | 4 |
| 2 | 2 |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
sssp_type: 'delta_stepping',
record_path: 1
}).stream() as p
where length(p) <> [0,3]
return p
Results: p
| 1--[102]--6--[107]--5 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2--[104]--3 |
| 1--[102]--6 |
| 1--[101]--2 |

