Overview
The HANP (Hop Attenuation & Node Preference) algorithm extends the traditional Label Propagation algorithm (LPA) by incorporating a label score attenuation mechanism and considering the influence of neighbor node degree on neighbor label weight. The goal of HANP is to improve the accuracy and robustness of community detection in networks, it was proposed in 2009:
- I.X.Y. Leung, P. Hui, P. Liò, J. Crowcroft, Towards real-time community detection in large networks (2009)
Concepts
Hop Attenuation
HANP associates each label with a score which decreases as it propagates from its origin. All labels are initially given a score of 1. Each time a node adopts new label from its neighborhood, a new attenuated score would be assigned to this new label by subtracting the hop attenuation δ (0 < δ < 1).
The hop attenuation mechanism limits the propagation of labels to nearby nodes and prevents them from spreading too broadly across the network.
Node Preference
In the calculation of the new maximal label, HANP incorporates node preference based on node degree. When node j ∈ Ni propagates its label L to node i, the weight of label L is calculated by:
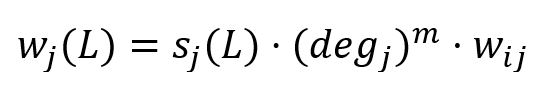
where,
- sj(L) is the score of label L in j.
- degj is the degree of j. When m > 0, more preference is given to node with high degree; m < 0, more preference is given to node with low degree; m = 0, no node preference is applied.
- wij is the sum of edge weights between i and j.
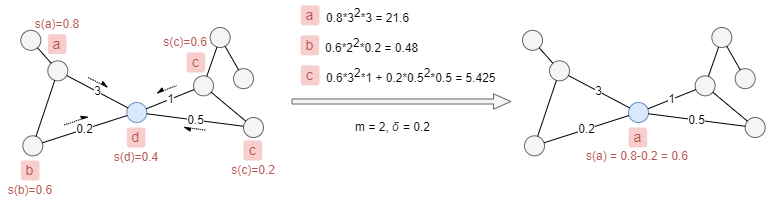
As the edge weights and label scores denoted in the example below, set m = 2 and δ = 0.2, the label of the blue node will be updated from d to a, and the score of label a in the blue node will be attenuated to 0.6.
Considerations
- HANP ignores the direction of edges but calculates them as undirected edges.
- Node with self-loops propagates its current label(s) to itself, and each self-loop is counted twice.
- When the selected label is equal to the current label, let δ = 0.
- HANP follows the synchronous update principle when updating node labels. This means that all nodes update their labels simultaneously based on the labels of their neighbors. The label score mechanism can prevent label oscillations.
- Due to factors such as the order of nodes, the random selection of labels with equal weights, and parallel calculations, the community division results of HANP may vary.
Syntax
- Command:
algo(hanp) - Parameters:
| Name | Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| node_label_property | @<schema>?.<property> |
Numeric/String type, must LTE | / | Yes | Node property to initialize node labels, nodes without the property are not involved in label propagation; UUID is used as label for all nodes if not set |
| edge_weight_property | @<schema>?.<property> |
Numeric type, must LTE | / | Yes | Edge property to use as edge weight |
| m | float | / | 0 |
Yes | The power exponent of the degree of neighbor node: when m > 0, more preference is given to node with high degree; m < 0, more preference is given to node with low degree; m = 0, no node preference is applied |
| delta | float | [0, 1] | 0 |
Yes | Hop attenuation δ |
| loop_num | int | ≥1 | 5 |
Yes | Number of propagation iterations |
| limit | int | ≥-1 | -1 |
Yes | Number of results to return, -1 to return all results |
Examples
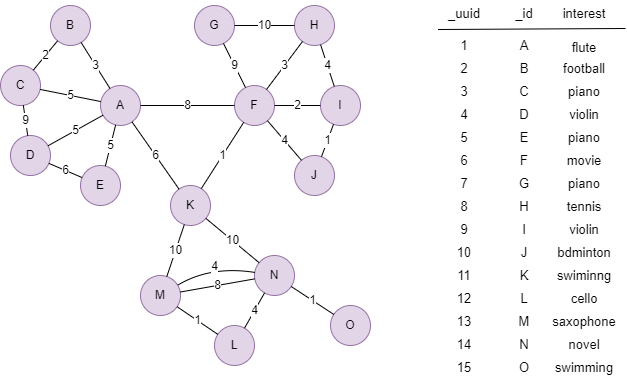
The example graph is as follows, nodes are of schema user, edges are of schema connect, the value of @connect.strength is shown in the graph:
File Writeback
| Spec | Content |
|---|---|
| filename | _id,label_1,score_1 |
algo(hanp).params({
loop_num: 10,
edge_weight_property: 'strength',
m: 2,
delta: 0.2
}).write({
file:{
filename: 'hanp'
}
})
Statistics: label_count = 4
Results: File hanp
O,13,-0.600000,
N,6,-1.000000,
M,6,-1.000000,
L,13,-0.600000,
K,13,-0.600000,
J,1,-0.200000,
I,1,-0.200000,
H,1,-0.200000,
G,1,-0.200000,
F,14,-1.000000,
E,6,-0.200000,
D,6,-0.200000,
C,6,-0.200000,
B,6,-0.200000,
A,6,-0.400000,
Property Writeback
Spec |
Content | Write to |
Data Type |
|---|---|---|---|
| property | label_1,score_1 |
Node property | Label: string,Label score: float |
algo(hanp).params({
node_label_property: '@user.interest',
m: 0.1,
delta: 0.3
}).write({
db:{
property: 'lab'
}
})
Statistics: label_count = 3
Results: The label and label score of each node is written to new properties lab_1 and score_1
Direct Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | []perNode | Node and its label, label score | _uuid, label_1, score_1 |
| 1 | KV | Number of labels | label_count |
algo(hanp).params({
loop_num: 12,
node_label_property: '@user.interest',
m: 1,
delta: 0.2
}) as res, stats
return res, stats
Results: res and stats
| _uuid | label_1 | score_1 |
|---|---|---|
| 15 | movie | -1.400000 |
| 14 | movie | -0.400000 |
| 13 | saxophone | -0.200000 |
| 12 | saxophone | -0.200000 |
| 11 | saxophone | -0.400000 |
| 10 | flute | -0.200000 |
| 9 | flute | -0.200000 |
| 8 | flute | -0.200000 |
| 7 | flute | -0.200000 |
| 6 | movie | -0.400000 |
| 5 | movie | -0.200000 |
| 4 | movie | -0.200000 |
| 3 | movie | -0.200000 |
| 2 | movie | -0.200000 |
| 1 | movie | -0.400000 |
| label_count |
|---|
| 3 |
Stream Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | []perNode | Node and its label, label score | _uuid, label_1, score_1 |
algo(hanp).params({
loop_num: 12,
node_label_property: '@user.interest',
m: 1,
delta: 0.2
}).stream() as hanp
group by hanp.label_1
with count(hanp) as labelCount
return table(hanp.label_1, labelCount)
order by labelCount desc
Results: table(hanp.label_1, labelCount)
| hanp.label_1 | labelCount |
|---|---|
| movie | 8 |
| flute | 4 |
| saxophone | 3 |
Stats Return
Alias Ordinal |
Type |
Description | Columns |
|---|---|---|---|
| 0 | KV | Number of labels | label_count |
algo(hanp).params({
loop_num: 5,
node_label_property: 'interest',
m: 0.6,
delta: 0.2
}).stats() as count
return count
Results: count
| label_count |
|---|
| 5 |

