Overview
The k-Means algorithm is a widely used clustering algorithm that aims to classify nodes in a graph into k clusters based on their similarity. The algorithm assigns each node to the cluster whose centroid is closest to it in terms of distance. The distance between a node and a centroid can be calculated using different distance metrics, such as Euclidean distance or cosine similarity.
The concept of the k-Means algorithm dates back to 1957, but it was formally named and popularized by J. MacQueen in 1967:
- J. MacQueen, Some methods for classification and analysis of multivariate observations (1967)
Since then, the algorithm has found applications in various domains, including vector quantization, clustering analysis, feature learning, computer vision, and more. It is often used as a preprocessing step for other algorithms or as a standalone method for exploratory data analysis.
Concepts
Centroid
The centroid or geometric center of an object in an N-dimensional space is the mean position of all the points in all of the N coordinate directions.
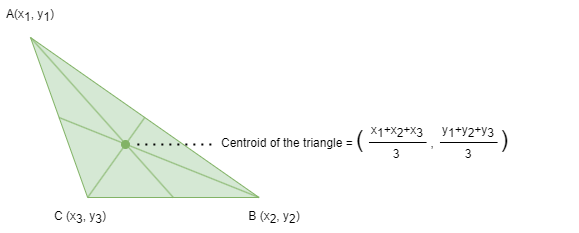
In the context of clustering algorithms like k-Means, a centroid refers to the geometric center of a cluster. By specifying several node properties as node features, centroid is the representative point that summarizes the features of the nodes within the cluster. To find the centroid of a cluster, the algorithm calculates the mean feature value for each dimension across all the nodes assigned to that cluster.
The algorithm begins with k nodes as initial centroids, which can be specified manually or sampled randomly by the system.
Distance Metrics
Ultipa's k-Means algorithm computes distance between a node and a centroid through Euclidean Distance or Cosine Similarity.
Clustering Iterations
During each iterative process of k-Means, each node in the graph calculates its distance to each of the cluster centroids and is assigned to the cluster of minimum distance from it. After organizing all nodes into clusters, the centroids are updated by recalculating their values based on the nodes assigned to the respective clusters.
The iteration ends when the clustering results stabilize to certain threshold, or the number of iterations reaches the limit.
Considerations
- The success of the k-Means algorithm depends on appropriately choosing the value of k and selecting appropriate distance metrics for the given problem. The selection of the initial centroids would also affect the final clustering results.
- If there are two or more same centroids exist, only one of them will take effect while the other equivalent centroids form empty clusters.
Syntax
- Command:
algo(k_means) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| start_ids | []_uuid |
/ | / | Yes | Specify nodes as the initial centroids, the length of UUID array must be equal to k; or let the system to choose if not set |
| k | int | [1, |V|] | 1 |
No | Number of desired clusters |
| distance_type | int | 1, 2 |
1 |
Yes | Type of the distance metric: 1 for Euclidean Distance, 2 for Cosine Similarity |
| node_schema_property | []@<schema>?.<property> |
Numeric type, must LTE | / | No | Two or more node properties to use as node features |
| loop_num | int | ≥1 | / | No | The maximum number of iterations |
Examples
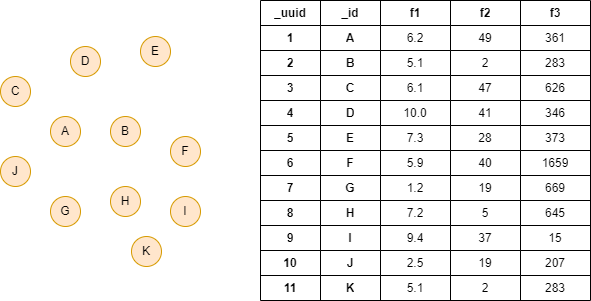
The example graph has 11 nodes (edges are ignored), and each node has properties f1, f2 and f3:
File Writeback
Spec |
Content |
|---|---|
| filename | community:_id,_id,... |
algo(k_means).params({
start_ids: [1,2,5],
k: 3,
distance_type: 2,
node_schema_property: ['f1', 'f2', 'f3'],
loop_num: 3
}).write({
file:{
filename: 'communities'
}
})
Results: File communities
0:I,
1:K,H,G,B,F,
2:J,C,A,E,D,
Direct Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perCommunity | Cluster and nodes in the cluster | community, uuids |
algo(k_means).params({
start_ids: [1,2,5],
k: 3,
distance_type: 1,
node_schema_property: ['@default.f1', '@default.f2', '@default.f3'],
loop_num: 3
}) as k3
return k3
Results: k3
| community | uuids |
|---|---|
| 0 | 11,5,4,2,1, |
| 1 | 10,9, |
| 2 | 8,7,6,3, |
Stream Return
| Alias Ordinal | Type | Description |
Columns |
|---|---|---|---|
| 0 | []perCommunity | Cluster and nodes in the cluster | community, uuids |
algo(k_means).params({
k: 2,
node_schema_property: ['f1', 'f2', 'f3'],
loop_num: 5
}).stream() as c
return c
Results: c
| community | uuids |
|---|---|
| 0 | 3,6,8,7, |
| 1 | 5,9,11,10,4,2,1, |

