Overview
A topological sorting of a directed graph is an ordering of its nodes into a sequence, where the start node of every edge appears before its end node. Topological sorting is applicable only to directed acyclic graphs (DAGs) that do not contain any cycles.
Topological sorting have various applications in computer science and other fields. In project management and job scheduling, topological sorting plays a crucial role in determining the optimal order of task execution based on their dependencies. It is also useful for resolving dependencies between modules, libraries, or components in software development. By utilizing this algorithm, dependencies can be resolved in the correct sequence, mitigating conflicts and potential errors.
Concepts
Directed Acyclic Graph (DAG)
A directed acyclic graph (DAG) is a type of directed graph with no directed cycles. That is, it is not possible to start at any node v and follow a directed path to return back to v in a DAG.
As shown here, the first and second graphs are DAGs, while the third graph does contain a directed cycle (B→C→D→B) and therefore does not qualify as a DAG.
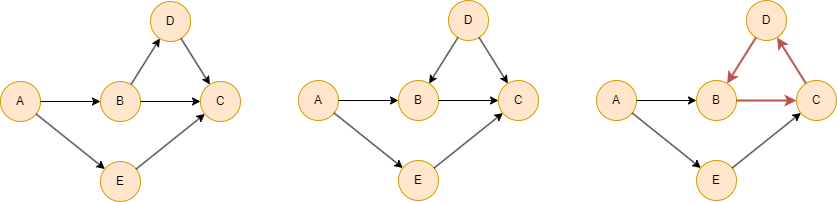
A directed graph is a DAG if and only if it can be topologically sorted.
Topological Sort
Every DAG has at least one topological sorting.
In the above examples, nodes in the first graph has 3 possible sortings:
- A, E, B, D, C
- A, B, E, D, C
- A, B, D, E, C
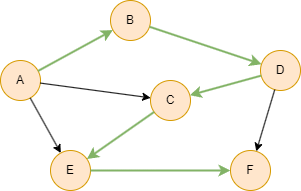
A DAG has a unique topological sorting if and only if it has a directed path containing all the nodes, in which case the sorting is the same as the order in which the nodes appear in the path.
In the following example, nodes only has 1 possible sorting: A, B, D, C, E, F.
Considerations
Running the Topogical Sort algorithm on a graph with cycles will cause the omitting of some nodes. The omitted nodes are:
- Nodes that are part of a cycle (including self-cycles).
- Nodes that are reachable from the above nodes through outgoing edges.
In the given example, first is to omit nodes C, D and G, which form the cycle. Then, nodes F, J and H which are reachable from them are also omitted. As a result, the topological sorting result is A, I, B, E.
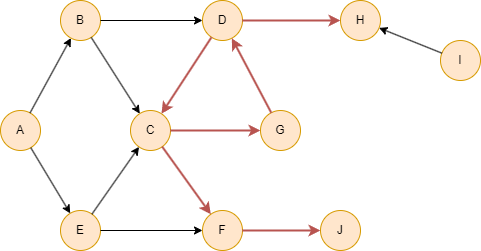
If a graph is disconnected, or becomes disconnected after omiting nodes that form the cycle and nodes influenced by them, the topological sorting is performed within each connected component. The sorting results are then returned consistently across all components. Isolated nodes are also included in the results and are not overlooked.
Syntax
- Command:
algo(topological_sort) - This algorithm has no parameters.
Examples
The example graph is as follows:
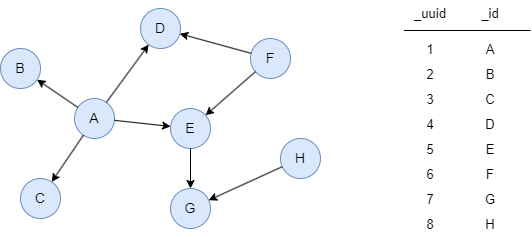
File Writeback
| Spec | Content |
|---|---|
| filename | _id,_id,... |
algo(topological_sort).params().write({
file: {
filename: 'sort'
}
})
Results: File sort
H
F
A
B
C
D
E
G
Direct Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []nodes |
Array of sorted nodes |
algo(topological_sort).params() as nodes
return nodes
Results: nodes
| 8 |
| 6 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 7 |
Stream Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []nodes |
Array of sorted nodes |
algo(topological_sort).params().stream() as n
find().nodes(n) as nodes
return nodes{*}
Results: nodes
| _id | _uuid |
|---|---|
| H | 8 |
| F | 6 |
| A | 1 |
| B | 2 |
| C | 3 |
| D | 4 |
| E | 5 |
| G | 7 |

