Overview
The k-hop clause khop().src().depth() retrieves the neighbor nodes a node can reach in K hops (through K edges) the shortest. These neighbors are commonly referred to as the k-hop neighbors of the source node.
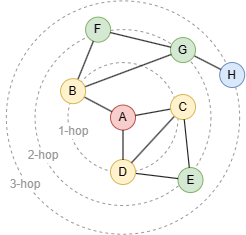
K-hop neighbor is one of the fundamental concepts in graph theory. In the graph above, nodes B, C and D are the 1-hop neighbors of node A, nodes E, F and G are the 2-hop neighbors of node A, and node H is the 3-hop neighbor of node A.
The value of k is unique and depends on the length of the shortest paths between two nodes. For example, although there are many paths exist between nodes A and C (A-C, A-D-C, A-D-E-C), the shortest distance is 1. Node C shouldn't appear in the results other than 1-hop neighbors.
The results of k-hop queries are deduplicated. For example, there are two shortest paths exist between nodes A and E, but E should only appear once in the 2-hop query of node A.
Ultipa's k-hop query adopts the BFS traversal technique to find the shortest paths and the k-hop neighbors. Optimizations have been applied to improve the performance of the k-hop query. It's recommended to use the k-hop query instead of other path query methods for the same purpose.
Syntax
- Clause alias: NODE type
- Methods:
Method |
Param Type |
Param Spec |
Required |
Description | Alias |
|---|---|---|---|---|---|
src() |
Filter | / | Yes | The conditions to specify the one and only one source node | NODE |
depth() |
Range | / | Yes | Depth for search (N≥1):depth(N): N hopsdepth(:N): 1~N hopsdepth(M:N): M~N hops (M≥0)When a range is set, the clause returns neighbor nodes in order from nearest to farthest |
N/A |
node_filter() |
Filter | / | No | The conditions to specify all nodes (other than the source node) in the querying paths | N/A |
edge_filter() |
Filter | / | No | The conditions to specify all edges in the querying paths | N/A |
direction() |
String | left, right |
No | Direction of all edges in the querying paths | N/A |
limit() |
Integer | ≥-1 | No | Number of results to return for each subquery, -1 signifies returning all |
N/A |
The exclusion of certain nodes or edges through
node_filter()oredge_filter()might induce structural change to the graph, potentially influencing the query outcomes. See examples under Node Filtering and Edge Filtering.
Examples
Example Graph
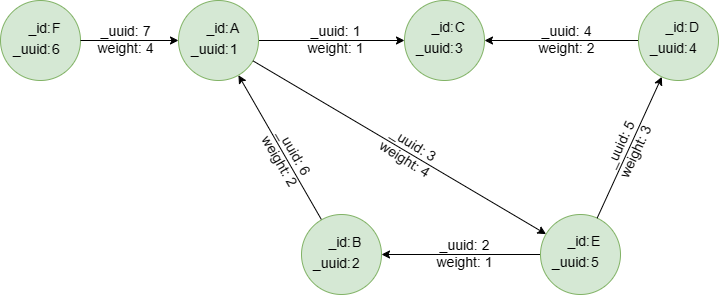
Run these UQLs row by row in an empty graphset to create this graph:
create().edge_property(@default, "weight", int32)
insert().into(@default).nodes([{_id:"A", _uuid:1}, {_id:"B", _uuid:2}, {_id:"C", _uuid:3}, {_id:"D", _uuid:4}, {_id:"E", _uuid:5}, {_id:"F", _uuid:6}])
insert().into(@default).edges([{_uuid:1, _from_uuid:1, _to_uuid:3, weight:1}, {_uuid:2, _from_uuid:5, _to_uuid:2 , weight:1}, {_uuid:3, _from_uuid:1, _to_uuid:5 , weight:4}, {_uuid:4, _from_uuid:4, _to_uuid:3 , weight:2}, {_uuid:5, _from_uuid:5, _to_uuid:4 , weight:3}, {_uuid:6, _from_uuid:2, _to_uuid:1 , weight:2}, {_uuid:7, _from_uuid:6, _to_uuid:1 , weight:4}])
Set Depth
Find the 3-hop neighbors of node D.
khop().src({_id == "D"}).depth(3) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| F | 6 |
Find 1-hop to 3-hop neighbors of node D.
khop().src({_id == "D"}).depth(:3) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| F | 6 |
| B | 2 |
| A | 1 |
| C | 3 |
| E | 5 |
Return Source Node
Find the 1- to 2-hop neighbors of node D. Return node D at the same time.
khop().src({_id == "D"}).depth(0:2) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| B | 2 |
| A | 1 |
| C | 3 |
| E | 5 |
| D | 4 |
Node Filtering
Find the 3-hop neighbors of node D while excluding node E.
khop().src({_id == "D"}).depth(3).node_filter({_id != "E"}) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| F | 6 |
| B | 2 |
When node E (and its adjacent edges) is excluded, node B becomes the 3-hop neighbor of node D.
Edge Filtering
Find the 3-hop neighbors of node D while excluding edge 5.
khop().src({_id == "D"}).depth(3).edge_filter({_uuid != 5}) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| E | 5 |
| F | 6 |
| B | 2 |
When edge 5 is excluded, node E and B become the 3-hop neighbor of node D.
Set Edge Direction
Find the 1- to 2-hop neighbors of node D while ensuring that all edges that pass through point to the right.
khop().src({_id == "D"}).depth(:2).direction(right) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| C | 3 |
Call Alias in src()
Find the 1-hop neighbors of nodes D and F.
find().nodes({_id in ["D", "F"]}) as start
khop().src(start).depth(1).direction(right) as n
return table(start._id, n._id)
Result:
| start._id | n._id |
|---|---|
| D | C |
| F | A |
Use limit()
Find three 1- to 3-hop neighbors of node D.
khop().src({_id == "D"}).depth(:3).limit(3) as n
return n{*}
Result:
| _id | _uuid |
|---|---|
| A | 1 |
| C | 3 |
| E | 5 |
The k-hop clause returns neighbor nodes in order from nearest to farthest, starting with 1-hop, followed by 2-hop, and then 3-hop.
Use OPTIONAL
Find the 2-hop neighbors of nodes A and D while ensuring that all edges that pass through point to the right. Return null if no neighbors are found.
find().nodes({_id in ["A", "D"]}) as start
optional khop().src(start).depth(2).direction(right) as n
return table(start._id, n._id)
Result:
| start._id | n._id |
|---|---|
| A | D |
| A | B |
| D | null |

