Ultipa Now Supports Vector Search

We are delighted to introduce Vector Search in the latest Ultipa Powerhouse (v5) - a critical capability to empower advanced similarity matchings in AI applications.

Vector Embedding

Vector embedding is a great way to capture meanings. Consider the following two paragraphs:

Paragraph A:

Imagine you're baking cookies and find a recipe that works perfectly. Instead of figuring it out from scratch each time, you keep the recipe so you can follow the same steps whenever you want more cookies. It saves time and ensures your cookies turn out just the way you like them.

Paragraph B:

When you discover a reliable way to solve a problem, saving that approach lets you tackle similar challenges faster in the future without starting from scratch.

These two paragraphs, though different in lengths and vocabulary, a human can easily link the metaphors and sees high-level similarity between them - the core idea of reusability of a proven solution. But how can computers mimic our understanding of language?

Traditional similarity analysis like Jaccard Similarity reply on surface-level overlap between word sets. After tokenizing (removing punctuation, lowering cases, filtering stop words, etc.), the two paragraphs yield:

Set A = [imagine, bake, cookie, recipe, work, perfectly, figure, scratch, time, keep, follow, step, want, save, ensure, turn, way, like]
Set B = [discover, reliable, solve, problem, save, approach, let, tackle, similar, challenge, fast, future, start, scratch, way]

The two sets share only 3 words ("scratch", "save", and "way") out of a combined 30. Jaccard Similarity is computed as the ratio of the size of the intersection of two sets and the size of their union:

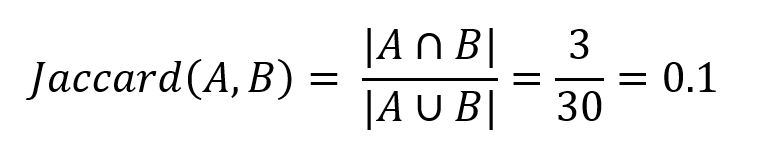
This low score (0.1) fails to reflect their semantic similarity.

To tackle this problem, the technique of vector embedding is developed to represent data – text and almost any kind of data, like images, videos, music, whatever – as points in a N-dimensional vector space. Each point is represented by N numbers, i.e.,(d₁,d₂, …, d_n), indicating its location in that space. Importantly, the closer two points are, the more similar they are.

For example, if we embed individual words into a 2-dimensional space, you will find that words like "cat" and "kitten", "computer" and "laptop", lie close together, while "computer" and "cat" are far apart.

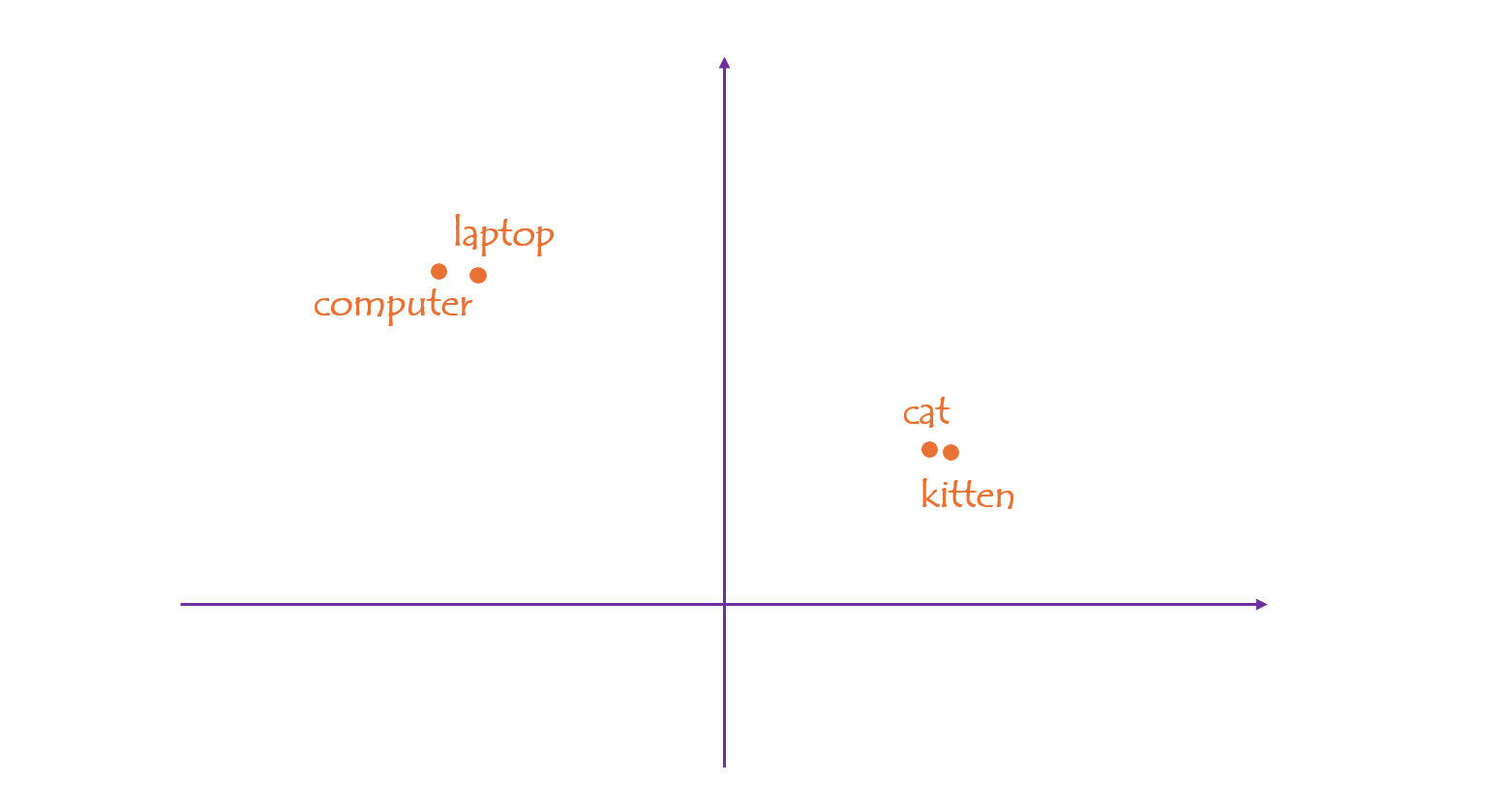
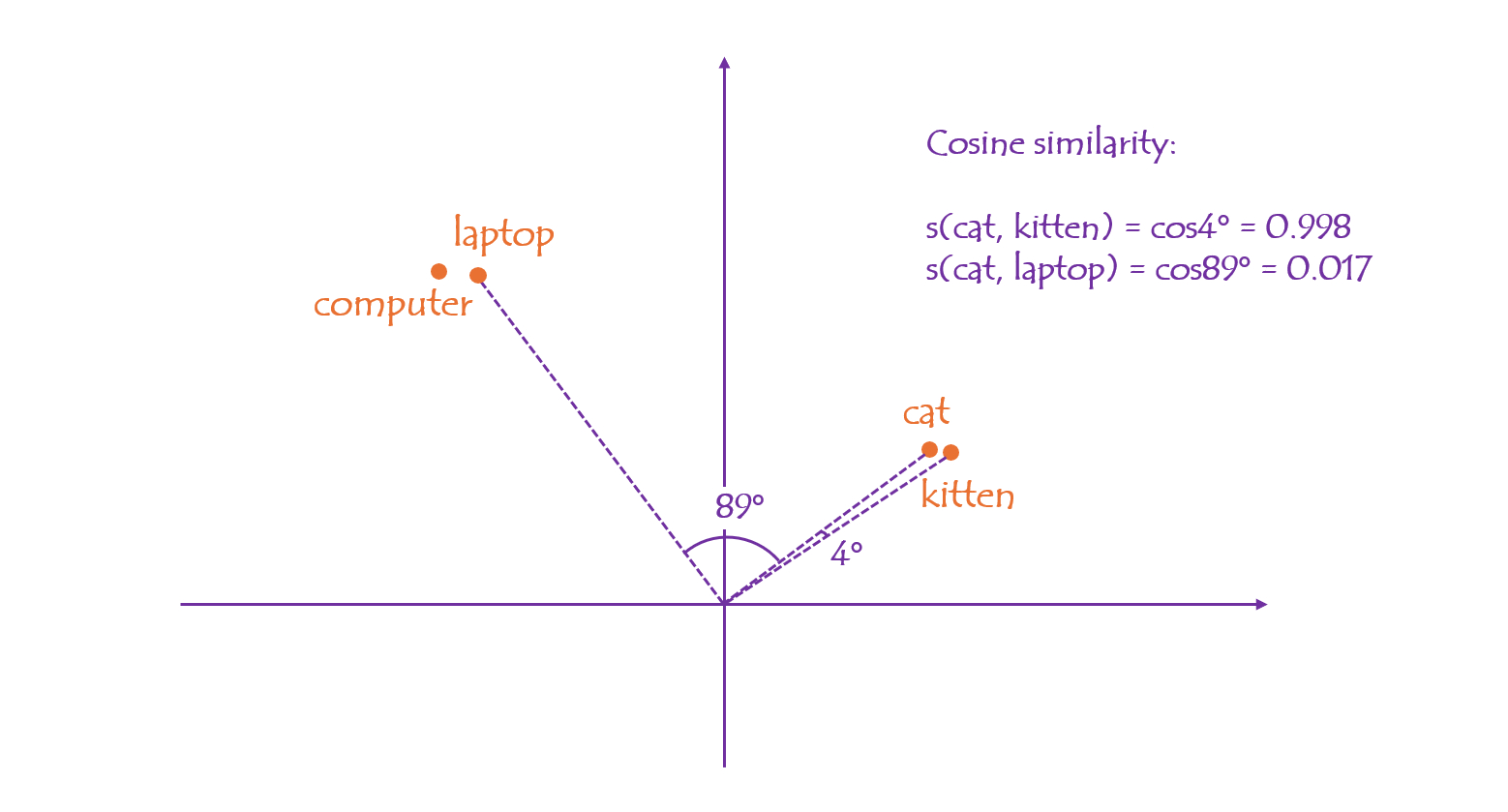
In a vector space, the proximity between points can be easily computed in various ways:

• Cosine Similarity uses the cosine value of the angle between two vectors (pointing from the origin to the point) to indicate their similarity. The cosine similarity between "cat" and "kitten” is 0.998, while "cat" and "laptop" is only 0.017.

• Euclidean distance of two points is the length of the straight line between them. The distance between "cat" and "kitten” is calculated as 0.151, while "cat" and "laptop" is 3.362.

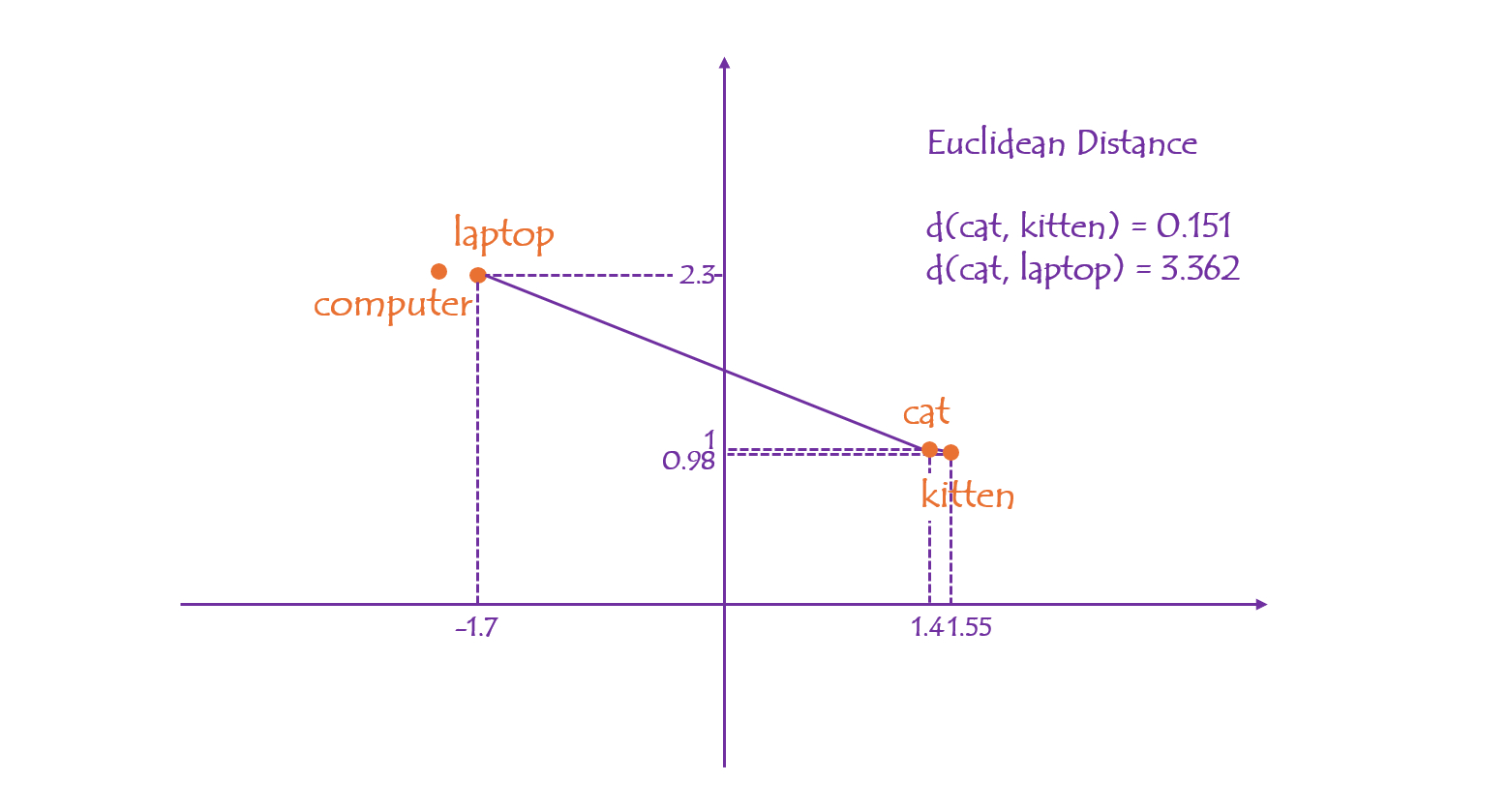
A 2D embedding is extremely limited. In real-world practices, the embedding dimensionality typically spans hundreds or thousands. High-dimensional embeddings capture rich and latent data features, leading to greater expressiveness. Though these spaces can’t be visualized directly like 2D, the underlying principle of proximity still holds.

What we haven’t covered yet is where vector embeddings come from. They are created through a machine learning process, where a model is trained to convert data into numeric embeddings. Many models have emerged, each typically specialized for a certain type of data.

We use a high-quality embedding model named e5-large-v2 by Intfloat, which is designed to produce sentence and document embeddings, to embed the two paragraphs given above. It outputs 1024-dimensional embeddings and the cosine similarity score between them is 0.882, which reflects high semantic similarity.

Python:

from sentence_transformers import SentenceTransformer
import numpy as np

model = SentenceTransformer("intfloat/e5-large-v2")
paragraphs = [    
    "Imagine you're baking cookies and find a recipe that works perfectly. Instead of figuring it out from scratch each time, you keep the recipe so you can follow the same steps whenever you want more cookies. It saves time and ensures your cookies turn out just the way you like them.",
     "When you discover a reliable way to solve a problem, saving that approach lets you tackle similar challenges faster in the future without starting from scratch."
]
embeddings = model.encode(paragraphs)
print("embedding_1 =", embeddings[0])
print("embedding_2 =", embeddings[1])

def cosine_similarity(a, b):    
    return np.dot(a, b) / (np.linalg.norm(a) * np.linalg.norm(b))

similarity = cosine_similarity(embeddings[0], embeddings[1])
print("Cosine similarity =", similarity)

Output:

embedding_1 = [ 0.00295209 -0.02910747 -0.00792895 ... -0.04337425 0.03010108 0.02038435]
embedding_2 = [ 0.00636229 -0.05014171 0.0041308 ... -0.03840123 0.03446656 0.02002169]
Cosine similarity = 0.88193464

Storing Vector Embeddings in Ultipa

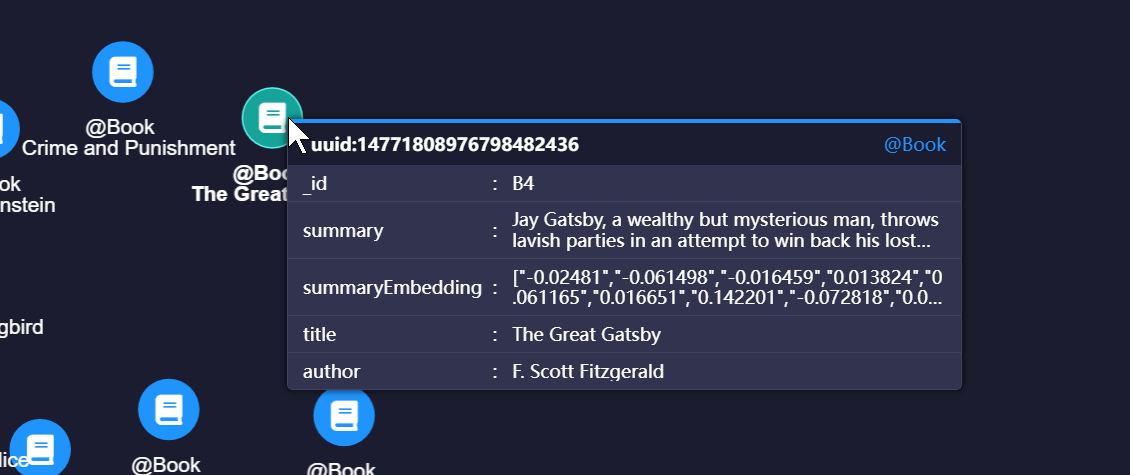
Ultipa allows you to store high-dimensional embeddings as properties of nodes or edges using list types (list<float> or list<double>).

For example, you can store the embeddings of book summaries in a property summaryEmbedding of Book nodes:

Performing Vector Search in Ultipa

Vector search, also known as vector similarity search, is to find the most similar items to a given item by comparing their vector embeddings. To make the vector search faster and more efficient, Ultipa also supports vector indexing.

Here’s how you create a vector index using GQL in Ultipa:

CREATE VECTOR INDEX "vIndex" ON NODE Book (summaryEmbedding)
OPTIONS {
    similarity_function: "COSINE",
    index_type: "HNSW",
    dimensions: 1024,
    vector_server: "vector_server_1"
}

This creates a vector index (named vIndex) for the summaryEmbedding property of Book nodes. Some configurations are required such as the similarity function, index type, and dimensions.

Now you can run a vector search like this:

MATCH (target:Book {title: "Pride and Prejudice"})
CALL vector.queryNodes("vIndex", 3, target.summaryEmbedding)
YIELD result
RETURN result

In this GQL query, the MATCH statement first specifies the target book, Pride and Prejudice, then the CALL statement invokes the created vector index (vIndex) to find the most similar 3 books whose summaryEmbedding is close to that of the target book.

For more information of vector search and index in Ultipa, refer to https://www.ultipa.com/docs/gql/vector-index.