Graph Database Benchmarks Demystified (Part 2)
June 30, 2022
Ricky Sun
Founder & CEO
Ultipa Inc.

This section is dedicated to query results validation of 3 types of operations:
- K-hop
- Shortest-Path
- Graph Algorithms
Let’s start with K-hop queries. First, let’s be clear of the definition of K-hop, there have been 2 types of K-hop:
- Kth-Hop Neighbors, which are exactly K hops away from the source vertex
- All Neighbors from the 1st Hop all the way to the Kth Hop
No matter which type of K-hop you are looking at, 2 essential points affect the correctness of the query:
- K-hop should be implemented using BFS, instead of DFS
- Results Deduplication: The results will not contain duplicated vertices on the same hop or across different hops (Many graph DBMS do have this dedup problem as we speak.)
Some vendors use DFS to find shortest paths, this approach has 2 fatal problems:
- Outright Wrong: There is a high probability that the results are wrong as DFS can’t guarantee a vertex belongs to the right hop (depth).
- Inefficient: On large and densely populated datasets, it’s impractical to traverse all possible paths, for instance, Twitter-2010 has many hotspot nodes having millions of neighbors, any 2-hop or deeper queries mean astronomical computational complexity!
Let’s validate the 1-Hop result of vertex ID=27960125 in Twitter-2010, first, we start from the source file which shows 8 edges (rows of connecting neighbors), but, what exactly is its 1-hop?
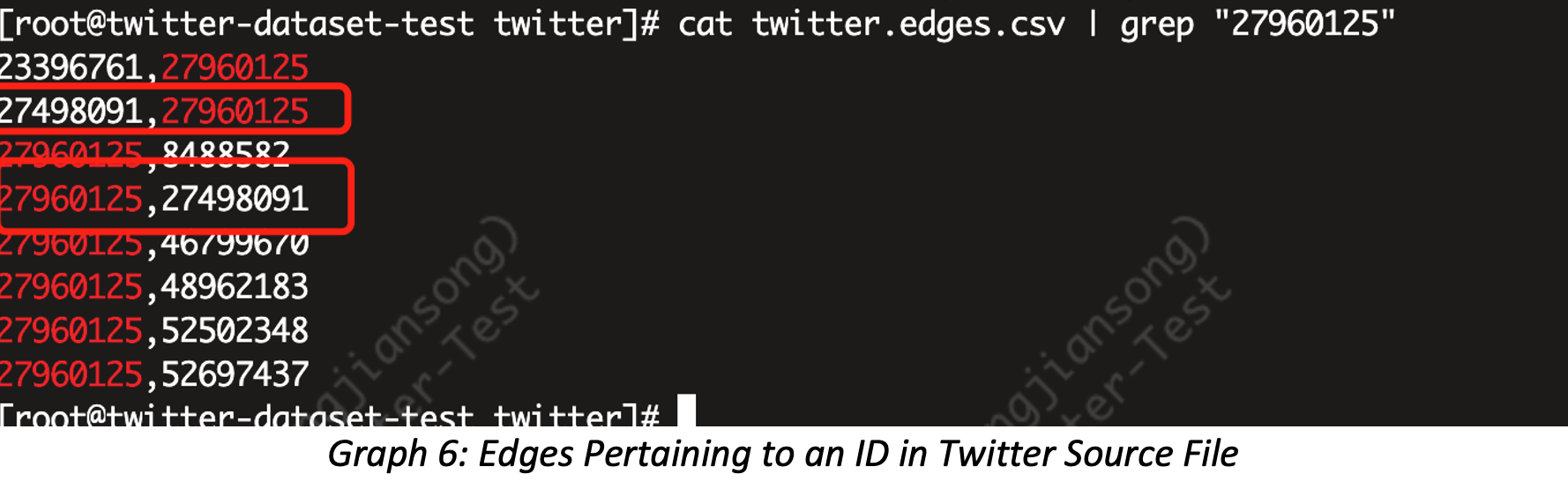
The correct answer is 7! Because the node 27960125 has a neighbor ID=27498091 which appears twice, because there are 2 edges in between these 2 vertices. If we deduplicate, we have 7.


To expand here on K-hop queries, it is possible to launch K-hop per edge direction, the screenshots below show 4 ways for running K-hop: regular bidirectional K-hop, outbound K-hop, inbound K-hop and K-hop with all neighbors. These queries combined can help validate any K-hop query.
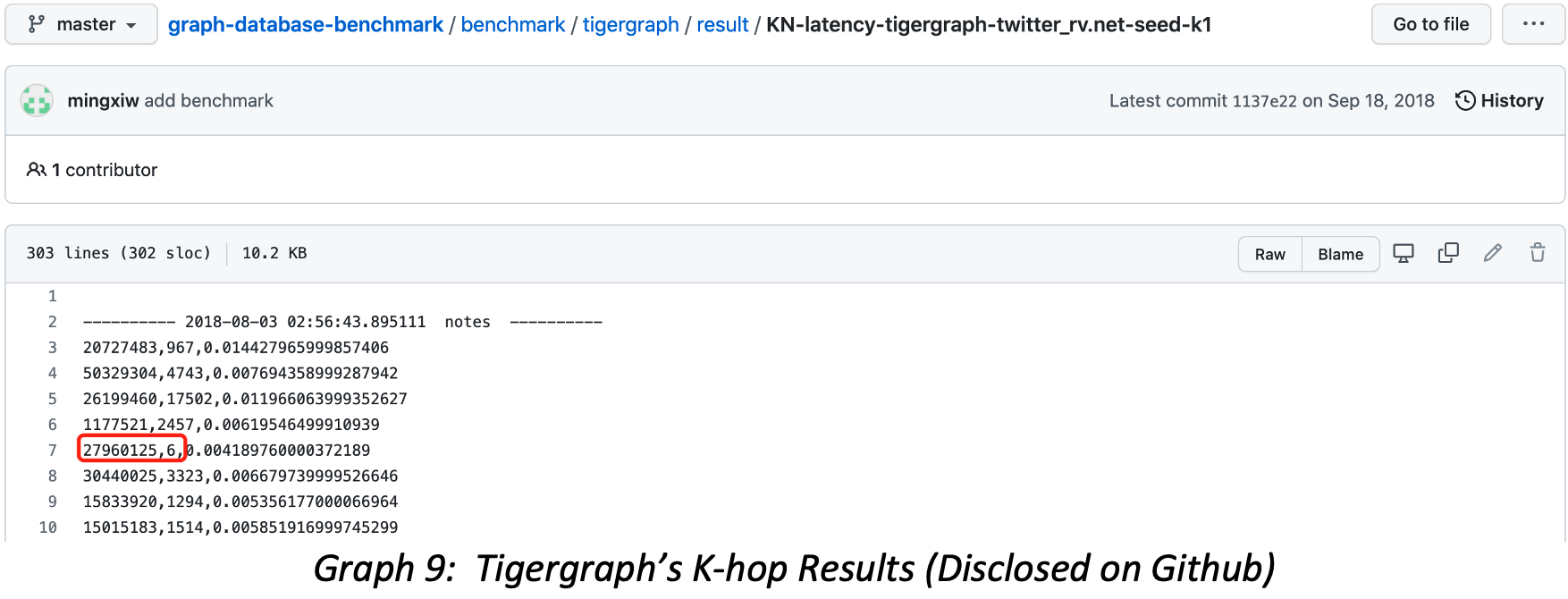
If we compare with publicly accessible Tigergraph’s K-hop query results, the vertex ID=27960125 has only 6 1-hop neighbors (shown in Graph 9), and the similar counting mistakes prevail throughout the entire published results on Github.
**********************
There are 3 possible causes for the Tigergraph K-hop problem:
- Data Modeling Mistake: Each edge is stored only once (unidirectionally), so that inverted edge traversal is impossible
- Query Method Mistake: The K-hop query is only conducted unidirectionally, instead of bidirectionally
- Code Implementation Bug: Such as results not being deduplicated, we’ll continue our examination in multiple hop queries later
Data modeling mistake is fatal, it means business logic will NOT be correctly reflected in the underpinning data models. Taking anti-fraud, AML or BI scenarios as an example, account A receives a transaction from account B, however, the system only stores an edge pointing from A to B (A-->B) but not the inverted edge from B to A (B<--A), this would make it impossible to trace the transaction starting from account B. This clearly is unacceptable.
Similarly, query method and coding-logic bugs are also serious, query should go bidirectionally instead of unidirectionally, the former is exponentially more complex when traversing multiple hops. The same holds true for storage space usage and data ingestion time.
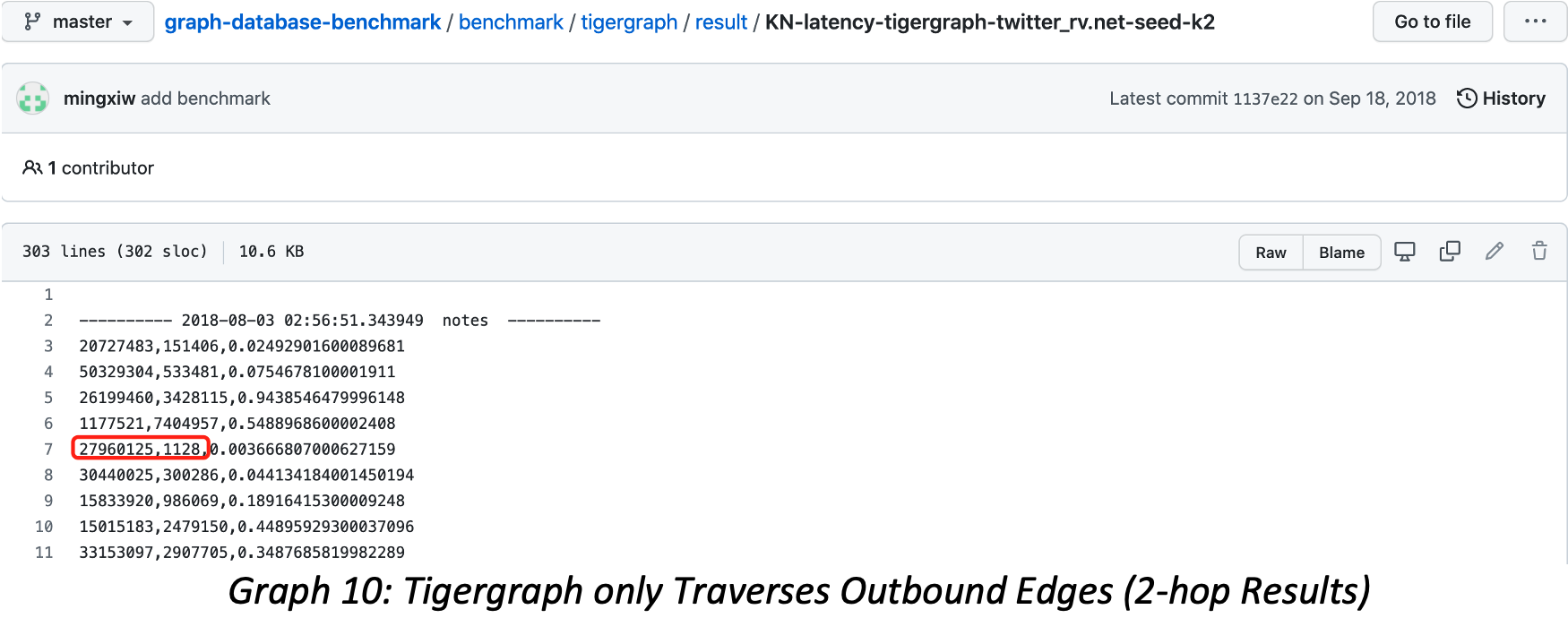
If we continue to track vertex ID=27960125’s 2-hop result, the Tigergraph’s mistakes become more dramatic yet more difficult to validate. Note Tigergraph returns 1128 neighbors, but there are duplicated neighbors, and the result is only based on outbound edges. The correct number of 2-Hop neighbors should be 533108, the difference here is 473 times, 47,300%! Tigergraph’s query results carry 3 mistakes simultaneously: data-modeling mistake, query method mistake and deduplication mistake.
Unfortunately, Tigergraph’s problem isn’t an exception, we are seeing similar problems with Neo4j, ArangoDB and other graph systems as well. For instance, Neo4j by default does NOT deduplicate K-hop results, if you force it to dedup, it will run exponentially slower. And, ArangoDB has a form of shortest-path query that returns only 1 path, which is fast but ridiculously wrong when there are many paths in the results pool.

Graph 11 shows 4 ways for conducting K-hop queries using Ultipa CLI, which helps validate query results with ease with precision.
GUI tools can help us visually and intuitively query and interact with the dataset and results. The screenshot below shows the 1-hop query results for a vertex with 13 neighbors.
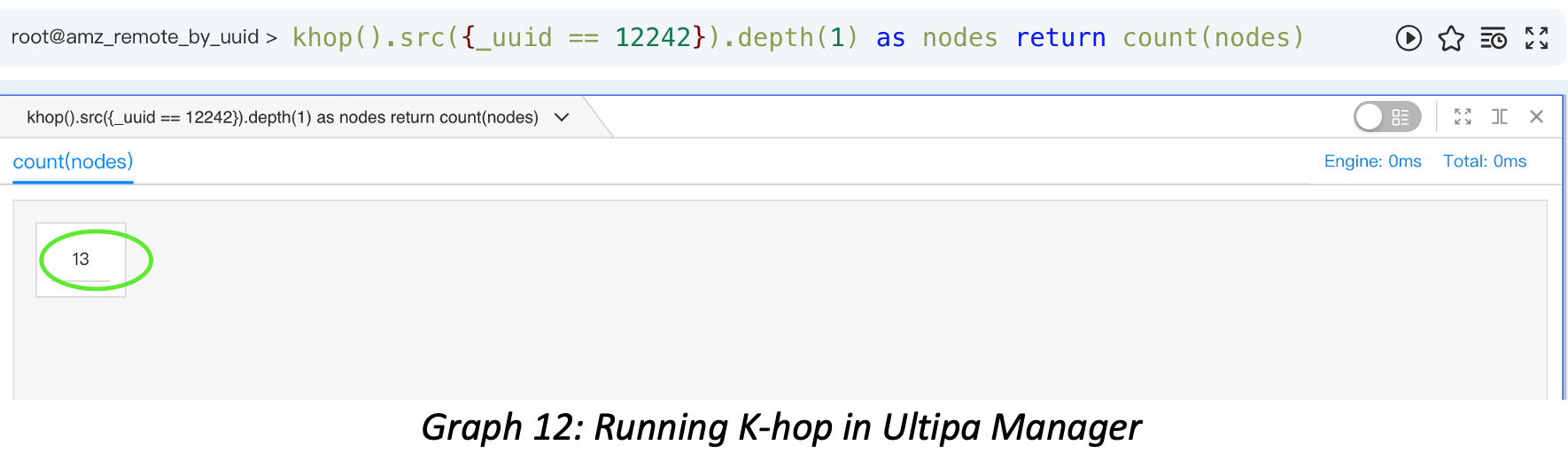
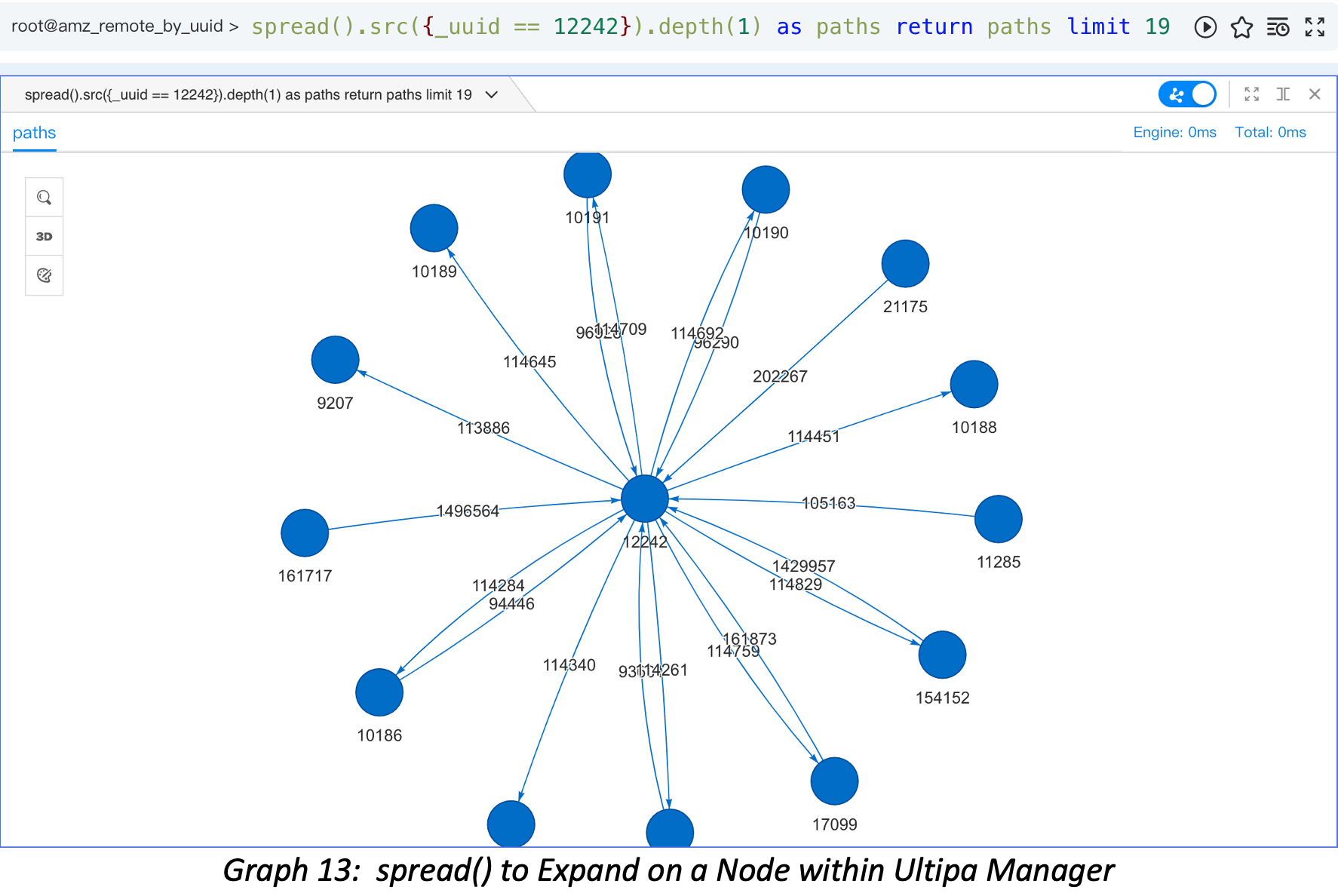
How to validate the results from above? A simple way is to expand on the vertex in BFS fashion and expand for only 1 layer (hop). The diagram below shows when expanding on the subject vertex using spread() function, it has 19 connecting edges, but the unique neighbors are only 13, after 6 edges are de-duplicated.
Now let’s address validations for shortest-path and graph algorithm.
We now know shortest-path is a special form of K-hop query, it’s different by 2 characteristics:
- High-dimensional results which are comprised of paths that are further composed of nodes and edges that are assembled in a certain sequence
- All paths are to be returned: Only calculating and returning 1 path is NOT enough. In financial fraud detection, AML, BI attribution analysis, there may exist many paths and returning just one is totally unacceptable.

The 2 diagrams above show that there are multiple shortest paths between ID 12 and 13 in Twitter dataset in regular (default) search mode, however, if you search by certain direction, you may get different answers as search filtering logic kicks in. For simple cases like this, you may grep the source file to find out that there are 2 bidirectional edges in between vertex ID 12 and 13, and if you do it recursively, you can validate more sophisticated queries. Note the keyword “recursively” I just used, it’s exactly why GQL/Graph-DBMS will be mainstream and SQL/RDBMS will fade away, because SQL’s weakest link is its inability to handle recursive queries, and GQL/Graph is automated on this.
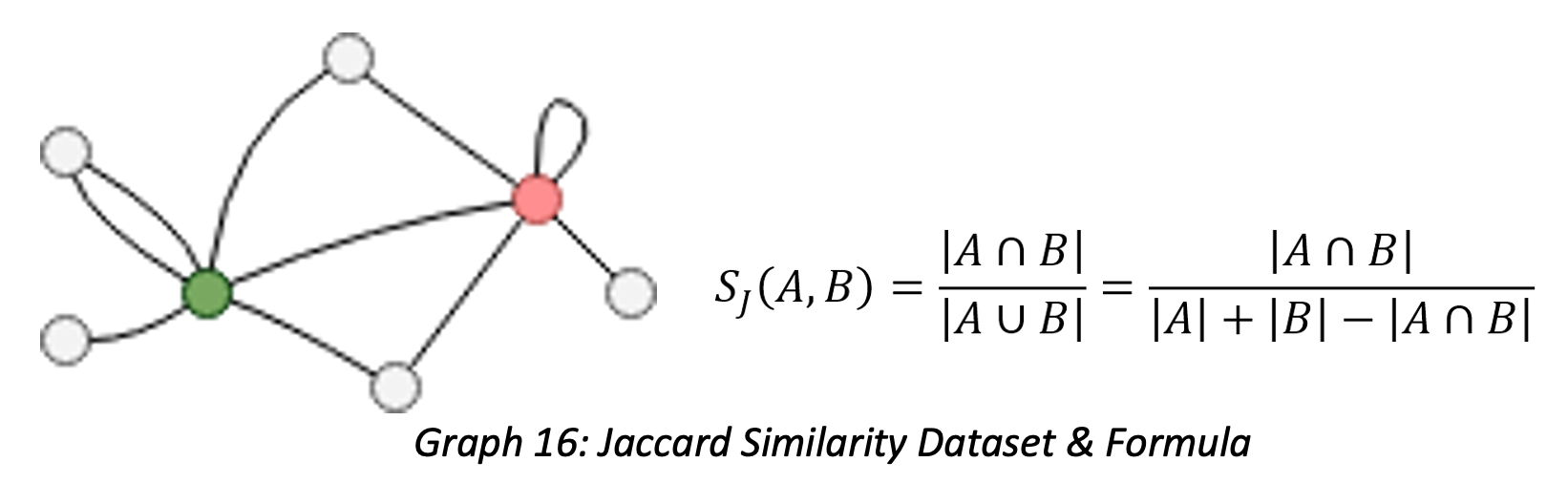
Next, we use Jaccard Similarity algorithm as an example to illustrate how to validate algorithm results. Taking the below diagram as an example, to calculate Jaccard Similarity of the green vertex and red vertex, you must find their common neighbors (2) and total neighbors (5), so that the similarity = 2/5 = 0.4 = 40%.
If the Jaccard Similarity algorithm is integrated, launching it directly will churn out the correct value of 0.4. If you desire to write several lines of GQL to implement it in an organic and white-box way, you can do this:

In Twitter-2010, computing Jaccard Similarity of any pair of vertices is to find each vertex’s 1-hop neighbors, taking ID=12 and ID=13 as an example, they both are hotspot supernodes having over 1 million neighbors, it would be impractical to validate the algorithm results manually. However, as long as you understand the logics under the hood of the algorithm, there are ways to divide and conquer it. The steps below show 2 ways to validate the algorithm:
- Launch the Jaccard algorithm:

- Validation Method 1: Using multiple GQLs to implement the Jaccard Similarity algorithm, the coding logic is the same as illustrated in Graph 17:

- Validation Method 2: First checking vertex ID 12 & 13’s 1-hop neighbors:

- Validation Method 2: Finding all distinct paths that are exactly 2-hop deep between ID 12 & 13, the number of paths is equal to the number of common neighbors of the two IDs:

- Validation Method 2: The similarity = Results-from-Step-4 / (12’s 1-hop + 13’s 1-hop – Results from step 4) = 15362638
- As you can see, the result from step 2 and step 5 are exact. We know the answer is right.
In this article, we traveled extra distance to give readers a comprehensive overview of how to read and digest a graph database system’s benchmark report, and methods to validate the results within. It’s utterly important to ensure the results are both complete and correct, after all, we are talking about data intelligence and infrastructure revolution, it would be pointless if a disruptive technology like graph DBMS can’t ensure the correctness of its data modeling or query results.