Overview
GraphSAGE (SAmple and aggreGatE) is a versatile inductive framework. Instead of training distinct embeddings for each node, it learns functions that generate embeddings by sampling and aggregating features from a node’s local neighborhood. This enables efficient generation of node embeddings for new data. GraphSAGE was proposed by W.H Hamilton et al. of Stanford University in 2017:
- W.L. Hamilton, R. Ying, J. Leskovec, Inductive Representation Learning on Large Graphs (2017)
The GraphSAGE algorithm is to produce node embeddings using a trained GraphSAGE model. The training process is outlined in GraphSAGE Train.
Concepts
Transductive and Inductive Framework
Most conventional graph embedding methods learn node embeddings by utilizing information from all nodes throughout the iterations. When new nodes are introduced to the network, the model must be retrained using the entire dataset. These transductive frameworks don't naturally extend to generalize.
GraphSAGE, on the other hand, acts as an inductive framework. It trains a collection of aggregator functions rather than creating individual embeddings for each node. This allows embeddings for newly added nodes to be derived based on the features and structural details of existing nodes, eliminating the need to reiterate the entire training procedure. This inductive capacity is crucial for high-throughput, operational machine learning systems.
GraphSAGE: Embedding Generation
Assume that we have already trained the parameters of K aggregator functions (denoted as AGGREGATEk) and K weight matrices (denoted as Wk). Let's now delve into the process of generating GraphSAGE embeddings (i.e., the forward propagation).
1. Neighborhood Sampling
In graph G = (V, E), for each target node to generate the embedding, sample some nodes from its 1st layer of neighborhood to the K-th layer of neighborhood:
- The number of nodes sampled at each layer is fixed as Sk (k = 1,2,...,K).
- Sampling proceeds from layer 1 to layer K, obtaining node sets Bk (k = K,...,1,0).
- Initialize BK with all target nodes.
- During sampling at the k-th layer, obtain set BK-k by taking the union of BK-k+1 and the collection of nodes sampled at layer k.
- The sampling is typically performed uniformly. If the number of neighbors at one layer is smaller than the set number, perform repeated sampling until the desired number of nodes is attained.
The creators of GraphSAGE observed that the value of K need not be large; practical success can be achieved even with modest values, such as K = 2, given that S1·S2 is below 500.
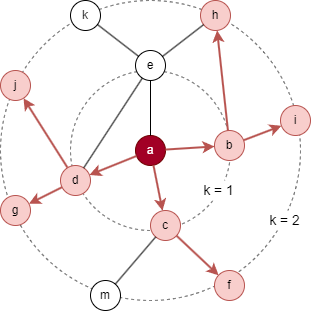
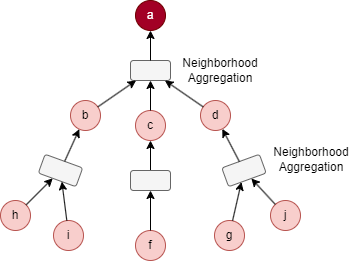
For the target node a in the above graph, considering the settings K = 2, S1 = 3, and S2 = 5. B2 is initialized as {a}.
- Sampling starts at the 1st layer: 3 immediate neighbors are selected, resulting N(a) = {b, c, d}, then B1 = B2 ⋃ N(a) = {a, b, c, d}.
- Next, sampling is performed at the 2nd layer: 5 neighbors are selcted based on nodes in N(a), resulting N(b) = {i, h}, N(c) = {f}, N(d) = {g, j}, this yields B0 = B1 ⋃ N(b) ⋃ N(c) ⋃ N(d) = {a, b, c, d, f, g, h, i, j}.
2. Feature Aggregation
For each node v ∈ B0, initialize their embedding vectors as their feature vectors:
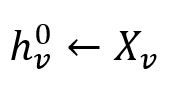
where each feature vector Xv is composed of several specified numeric property values of the node.
The final embeddings of the target nodes are computed through K iterations. In the k-th (k = 1,2,...,K) iteration, for each node v ∈ Bk:
- Aggregate the (k-1)-th vectors of its sampled neighbors into a neighborhood vector, using the aggregator function AGGREGATEk.
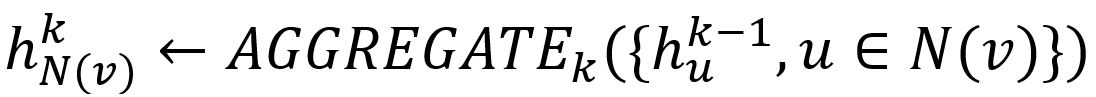
- Concatenate its (k-1)-th vector with the aggregated neighborhood vector. This concatenated vector is then refined by going through a fully connected layer weighted by matrix Wk, followed by a non-linear activation function σ (e.g., Sigmoid, ReLu).
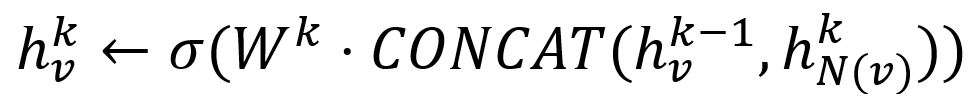
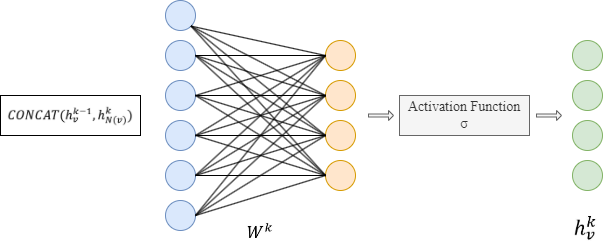
- Normalize :
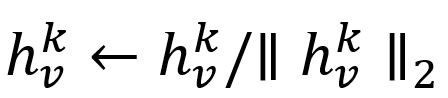
The process of feature aggregation of our example can be illustrated as below:
| 1st Iteration | 2nd Iteration |
|---|---|
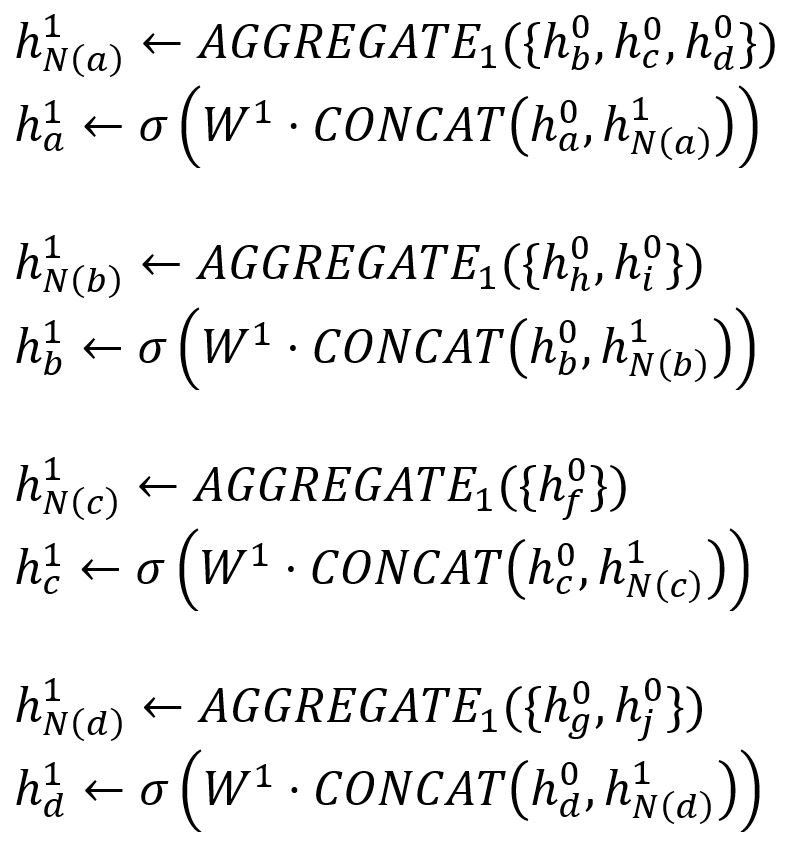 |
 |
Considerations
- The GraphSAGE algorithm ignores the direction of edges but calculates them as undirected edges.
Syntax
- Command:
algo(graph_sage) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| model_task_id | int | / | / | No | Task ID of the GraphSAGE Train algorithm that trained the model |
| ids | []_id |
/ | / | Yes | ID of the nodes to generate embeddings; generate for all nodes if not set |
| node_property_names | []<property> |
Numeric type, must LTE | Read from the model | Yes | Node properties to form the feature vectors |
| edge_property_name | <property> |
Numeric type, must LTE | Read from the model | Yes | Edge property to use as edge weight; edges are unweighted if not set |
| sample_size | []int | / | Read from the model | Yes | Elements in the list are the number of nodes sampled at layer K to layer 1 respectively; the size of the list is the number of layers |
Examples
Property Writeback
| Spec | Content | Write to | Data Type |
|---|---|---|---|
| property_name | Node embedding | Node property | string |
algo(graph_sage).params({
model_task_id: 4785,
ids: ['ULTIPA8000000000000001', 'ULTIPA8000000000000002']
}).write({
db:{
property_name: 'embedding_graphSage'
}
})
Results: Embedding for each node is written to a new property named embedding_graphSage

