Overview
The GraphSAGE Train algorithm is employed to train the GraphSAGE model. The training process occurs in a fully unsupervised setting and involves the use of techniques such as SGD and backpropagation techniques.
The trained GraphSAGE model can be used to generate node embeddings. This inductive framework is also capable of producing embeddings for newly joined nodes without necessitating model re-training. For detailed information on how to use GraphSAGE model for this purpose, please refer to the GraphSAGE algorithm.
Concepts
GraphSAGE: Learning the Parameters
According to the embedding generation (forward propagation) algorithm of GraphSAGE, we need to tune the parameters of K aggregator functions (denoted as AGGREGATEk) and K weight matrices (denoted as Wk).
The loss function is designed to encourages nearby nodes to have similar embeddings, while enforcing the embeddings of disparate nodes to be highly distinct:
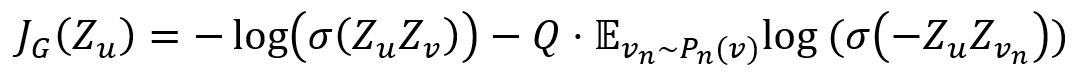
where,
- v is a node that co-occurs near u on fixed-length random walk.
- vn is a negative sample, Q is the number of negative samples, Pn is the negative sampling distribution.
- σ is the sigmoid function.
- Z is the embedding of node generated from the GraphSAGE model.
In cases where embeddings are to be used on a specific downstream task, this loss function can simply be replaced, or augmented, by a task-specific objective (e.g., cross-entropy loss).
Aggregator Functions
An aggregator function combines a set of vectors into a single vector, it is used to produce the neighborhood vector in GraphSAGE. There are two types of aggregators supported.
1. Mean Aggregator
The mean aggregator simply takes the elementwise mean of the vectors. For example, vectors [1,2], [4,3] and [3,4] will be aggregated into vector [2.667,3].
When it is used, the embedding generation algorithm of GraphSAGE directly calculates the k-th embedding of the node:

2. Pooling Aggregator
In pooling approach, each neighbor’s vector is independently fed through a fully connected neural network; following this transformation, an elementwise max-pooling operation is applied to aggregate information across the neighbor set:
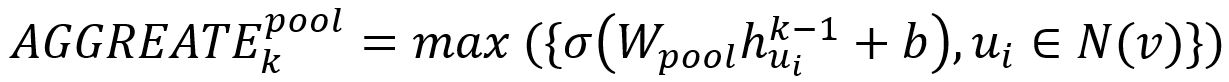
where max denotes the element-wise max operator and σ is a non-linear activation function.
Considerations
- The GraphSAGE Train algorithm ignores the direction of edges but calculates them as undirected edges.
Syntax
- Command:
algo(graph_sage_train) - Parameters:
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| dimension | int | ≥2 | 64 |
Yes | Dimension of the generated node embeddings |
| node_property_names | []<property> |
Numeric type, must LTE | / | No | Node properties to form the feature vectors |
| edge_property_name | <property> |
Numeric type, must LTE | / | Yes | Edge property to use as edge weight; edges are unweighted if not set |
| search_depth | int | ≥1 | 5 |
Yes | Maximum depth of the random walk |
| sample_size | []int | / | [25, 10] |
Yes | Elements in the list are the number of nodes sampled at layer K to layer 1 respectively; the size of the list is the number of layers |
| learning_rate | float | [0, 1] | 0.1 |
Yes | Learning rate of each training iteration |
| epochs | int | ≥1 | 10 |
Yes | Number of large training cycles; neighborhood sampling is re-done for each epoch |
| max_iterations | int | ≥1 | 10 |
Yes | Maximum training iterations per epoch; each iteration one batch is selected randomly to calculate gradient and update parameters |
| tolerance | double | >0 | 1e-10 |
Yes | The current epoch ends when the values of the loss function between iterations is less than this tolerance |
| aggregator | string | mean, pool |
mean |
Yes | The aggregator to be used |
| batch_size | int | ≥1 | Number of nodes/threads | Yes | Number of nodes per batch; this is also used as the number of negative samples |
Examples
File Writeback
| Spec | Content |
|---|---|
| model_name | The trained GraphSAGE model |
algo(graph_sage_train).params({
dimension: 10,
node_property_names: ['dbField','fField','uInt32','int32','age'],
edge_property_name: 'rank',
search_depth: 5,
sample_size: [25,10],
learning_rate: 0.05,
epochs: 8,
max_iterations: 10,
tolerance: 1e-10,
aggregator: 'mean',
batch_size: 100
}).write({
file:{
model_name: 'SAGE_model'
}
})
Results: File SAGE_model.json; this model can be used in the GraphSAGE algorithm to generate node embeddings

