Vue d’ensemble
L'algorithme Shortest Path Faster (SPFA) est une amélioration de l'algorithme de Bellman-Ford qui calcule le plus court chemin entre un node source et tous les nodes accessibles (c'est-à-dire les plus courts chemins à source unique) dans un graph. L'algorithme convient particulièrement aux graphs qui contiennent des edges de poids négatif.
L'algorithme SPFA a été d'abord publié par E.F. Moore en 1959, mais le nom, "Shortest Path Faster Algorithm (SPFA)", a été donné par FanDing Duan, qui redécouvrit l'algorithme en 1994.
- F. Duan, 关于最短路径的SPFA快速算法 [À propos de l'algorithme SPFA] (1994)
Concepts
Algorithme Shortest Path Faster (SPFA)
Étant donné un graph G = (V, E) et un node source s∈V, le tableau d[] est utilisé pour stocker les distances des plus courts chemins de s à tous les nodes. Initialisez tous les éléments de d[] avec l'infini, sauf pour d[s] = 0.
L'idée de base de SPFA est la même que celle de l'algorithme de Bellman-Ford en ce que chaque node est utilisé comme candidat pour détendre ses nodes adjacents. L'amélioration par rapport à ce dernier est que, au lieu d'essayer tous les nodes de manière inutile, SPFA maintient une file d'attente premier entré, premier sorti Q pour stocker les nodes candidats et n'ajoute un node à la file que s'il est détendu.
Le terme relaxation se réfère au processus de mise à jour de la distance d'un node v connectée au node u à une distance potentiellement plus courte en considérant le chemin à travers le node u. Spécifiquement, la distance du node v est mise à jour à d[v] = d[u] + w(u,v), où w(u,v) est le poids du edge (u,v). Cette mise à jour est effectuée uniquement si le d[v] courant est supérieur à d[u] + w(u,v).
Au début de l'algorithme, tous les nodes ont comme distance l'infini sauf le node source qui est à 0. Le node source est considéré comme détendu pour la première fois et poussé dans la file d'attente.
À chaque itération, SPFA retire un node u de Q en tant que candidat. Pour chaque edge (u,v) dans le graph, si le node v peut être détendu, les étapes suivantes sont effectuées :
- Détendre le node v: d[v] = d[v] + w(u,v).
- Pousser le node v dans Q si v n'est pas dans Q.
Ce processus se répète jusqu'à ce qu'aucun node ne puisse plus être détendu.
Les étapes ci-dessous illustrent comment calculer le SPFA avec le node source A et trouver les plus courts chemins pondérés dans la direction sortante :
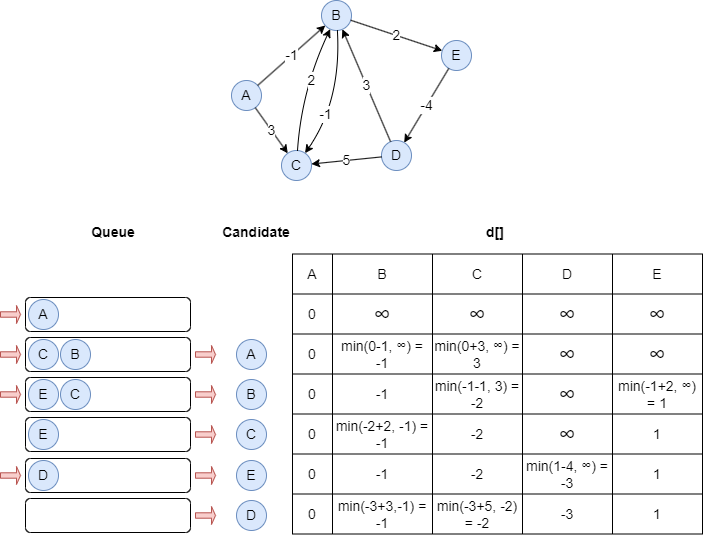
Considérations
- SPFA peut manipuler des graphs avec des poids négatifs sous les conditions que (1) le node source ne peut accéder à aucun node dans un cycle négatif, et (2) les plus courts chemins sont dirigés. Un cycle négatif est un cycle où la somme des poids des edges est négative. Lorsque des cycles négatifs sont présents ou que les plus courts chemins sont non dirigés lorsque des poids négatifs existent, l'algorithme produira des résultats infinis. Cela se produit parce qu'il traverse de manière répétée le cycle négatif ou l'edge négatif, conduisant à des coûts continuellement décroissants à chaque parcours.
- Si plusieurs plus courts chemins existent entre deux nodes, tous seront trouvés.
- Dans des graphs déconnectés, l'algorithme ne produit que les plus courts chemins du node source à tous les nodes appartenant à la même composante connectée que le node source.
Syntaxe
- Commande :
algo(sssp) - Paramètres :
Nom |
Type |
Spécification |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | _id / _uuid |
/ | / | No | ID/UUID du node source unique |
| direction | string | in, out |
/ | Oui | Direction du plus court chemin, ignorer la direction de l'edge si non défini |
| edge_schema_property | []@schema?.property |
Type numérique, doit être LTE | / | Oui | Une ou plusieurs edge properties à utiliser comme poids des edges, où les valeurs de plusieurs properties sont additionnées ; considérer le graph comme non pondéré si non défini |
| record_path | int | 0, 1 |
0 |
Oui | 1 pour retourner les plus courts chemins, 0 pour retourner les plus courtes distances |
| sssp_type | string | spfa |
dijkstra |
Non | Pour exécuter le SPFA, laissez spfa |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par la plus courte distance depuis le node source |
Exemples
Le graph d'exemple est le suivant :
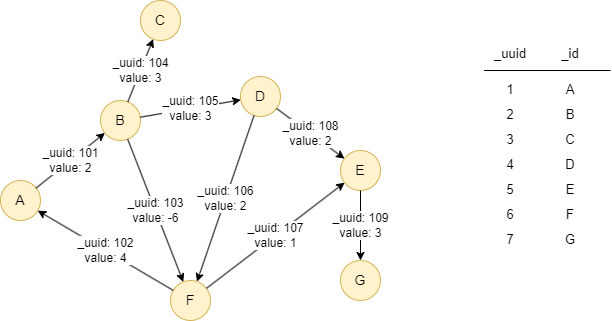
File Writeback
| Spécification | record_path |
Content | Description |
|---|---|---|---|
| filename | 0 | _id,totalCost |
La plus courte distance/coût du node source à chaque autre node |
| 1 | _id--_uuid--_id |
Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'ID alterné des nodes et l'UUID des edges qui forment le chemin |
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
direction: 'out',
sssp_type: 'spfa'
}).write({
file: {
filename: 'costs'
}
})
Résultats : Fichier costs
A,0
B,2
C,5
D,5
E,-3
F,-4
G,0
algo(sssp).params({
uuids: 1,
edge_schema_property: '@default.value',
direction: 'out',
sssp_type: 'spfa',
record_path: 1
}).write({
file: {
filename: 'paths'
}
})
Résultats : Fichier paths
A--[101]--B--[104]--C
A--[101]--B--[105]--D
A--[101]--B
A
A--[101]--B--[103]--F--[107]--E--[109]--G
A--[101]--B--[103]--F--[107]--E
A--[101]--B--[103]--F
Direct Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | La plus courte distance/coût du node source à chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'UUID alterné des nodes et l'UUID des edges qui forment le chemin | / |
algo(sssp).params({
uuids: 1,
edge_schema_property: 'value',
sssp_type: 'spfa',
record_path: 0,
direction: 'in'
}) as costs
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 1 | 0 |
| 2 | -2 |
| 4 | 6 |
| 6 | 4 |
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
sssp_type: 'spfa',
direction: 'in',
record_path: 1
}) as paths
return paths
Résultats : paths
| 1--[102]--6--[106]--4 |
| 1--[102]--6 |
| 1 |
| 1--[102]--6--[103]--2 |
Stream Return
| Alias Ordinal | record_path |
Type | Description | Colonnes |
|---|---|---|---|---|
| 0 | 0 | []perNode | La plus courte distance/coût du node source à chaque autre node | _uuid, totalCost |
| 1 | []perPath | Le plus court chemin du node source à chaque autre node, le chemin est représenté par l'UUID alterné des nodes et l'UUID des edges qui forment le chemin | / |
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
sssp_type: 'spfa',
direction: 'out'
}).stream() as costs
where costs.totalCost < 0
return costs
Résultats : costs
| _uuid | totalCost |
|---|---|
| 5 | -3 |
| 6 | -4 |
algo(sssp).params({
ids: 'A',
edge_schema_property: '@default.value',
sssp_type: 'spfa',
direction: 'out',
record_path: 1
}).stream() as p
where length(p) <> [0,3]
return p
Résultats : p
| 1--[101]--2--[104]--3 |
| 1--[101]--2--[105]--4 |
| 1--[101]--2 |
| 1--[101]--2--[103]--6 |

