Vue d’ensemble
L'algorithme HyperANF (Hyper-Approximate Neighborhood Function) est utilisé pour évaluer la distance moyenne dans un graph. Il offre un compromis entre précision et efficacité computationnelle, ce qui le rend adapté aux graphes de grande taille où calculer la distance moyenne exacte peut être irréalisable ou chronophage.
Matériel connexe de l'algorithme :
- P. Boldi, M. Rosa, S. Vigna, HyperANF: Approximating the Neighbourhood Function of Very Large Graphs on a Budget (2011)
Concepts
Distance Moyenne dans un Graph
La distance moyenne dans un graph est une métrique utilisée pour mesurer le nombre moyen d'étapes ou d'arêtes nécessaires pour se déplacer entre n'importe quelles deux nodes dans un graph. Elle quantifie la connectivité globale ou la proximité des nodes dans le graph.
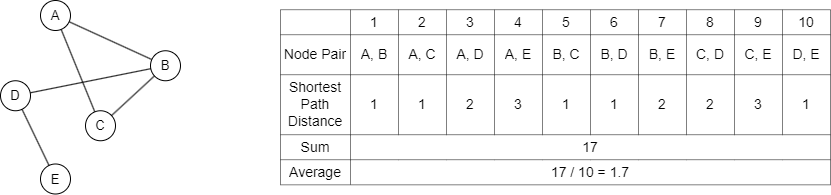
Comme montré ci-dessus, la distance moyenne dans un graph est généralement calculée en effectuant une traversée de graph pour calculer la distance du plus court path entre chaque paire de nodes, puis en additionnant les distances et en divisant par le nombre total de paires de nodes pour obtenir la moyenne.
Fonction de Voisinage Approximative (ANF)
Les traversées de graph peuvent être coûteuses en termes de calcul et gourmandes en mémoire, surtout pour les graphes de grande échelle. Dans de tels cas, les algorithmes de fonction de voisinage approximative (ANF) sont couramment utilisés pour estimer de manière plus efficace la distance moyenne dans un graph.
Les algorithmes ANF visent à estimer la fonction de voisinage (NF) :
- La fonction de voisinage (NF) d'un graph, notée
N(t), renvoie le nombre de paires de nodes telles que les deux nodes peuvent se joindre en t étapes ou moins. - La fonction de voisinage individuelle (INF) d'un node x dans un graph, notée
N(x,t), renvoie le nombre de nodes pouvant être atteints à partir de x avec t étapes ou moins. - Dans un graph non dirigé G = (V, E), la relation entre NF et INF est :
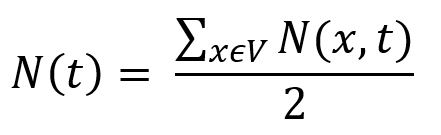
La NF peut aider à révéler certaines caractéristiques des graphes, y compris la distance moyenne dans un graph:
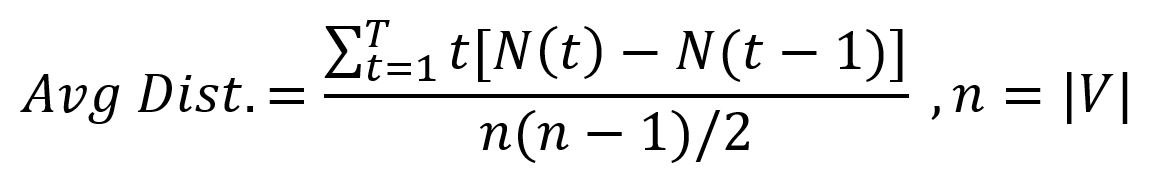
Le calcul du graph d'exemple ci-dessus est montré ci-dessous :

Cependant, il est très coûteux de calculer la NF exactement sur de grands graphes. En approximant la fonction de voisinage, les algorithmes ANF peuvent estimer la distance moyenne dans un graph sans parcourir l'ensemble du graph.
Compteur HyperLogLog
Le compteur HyperLogLog est utilisé pour compter approximativement le nombre d'éléments distincts (c'est-à-dire la cardinalité) dans un grand ensemble ou flux d'éléments. Calculer la cardinalité exacte nécessite souvent une quantité de mémoire proportionnelle à la cardinalité, ce qui est impraticable pour des ensembles de données très larges. HyperLogLog prend significativement moins de mémoire, avec une complexité spatiale de O(log(log n)) (c'est la raison pour laquelle ces compteurs sont appelés HyperLogLog).
Un compteur HyperLogLog peut être vu comme un tableau de m = 2b registres, et chaque registre est initialisé à -∞. Par exemple, b = 3, donc M[0] = M[1] = ... = M[7] = -∞.
Le nombre de registres dépend de la précision souhaitée de l'estimation. Plus de registres peuvent fournir une estimation plus précise, mais nécessitent également plus de mémoire.
D'abord, chaque élément x de l'ensemble est mappé en une séquence binaire de taille fixe par une fonction de hachage h(). Par exemple, h(x) = 0100001110101....
Ensuite, mettre à jour les registres. Pour chaque élément x de l'ensemble :
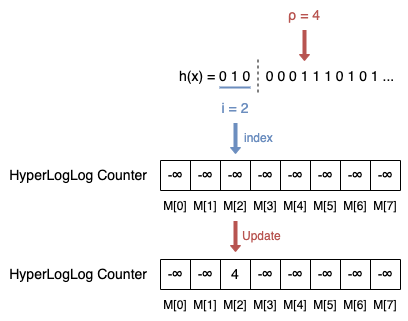
- Calculer l'indice i du registre par la valeur entière des b bits les plus à gauche de h(x), c'est-à-dire hb(x). Dans l'exemple, i = hb(x) = 010 = 0*22 + 1*21 + 0*20 = 2.
- Laisser hb(x) être la séquence de bits restants de h(x), et ρ(hb(x)) être la position du 1 le plus à gauche de hb(x). Dans l'exemple, ρ(hb(x)) = ρ(0001110101...) = 4.
- Mettre à jour le registre M[i] = max(M[i], ρ(hb(x))). Dans l'exemple, M[2] = max(-∞, 4) = 4.
Après avoir lu tous les éléments, la cardinalité est calculée par le compteur HyperLogLog comme suit :
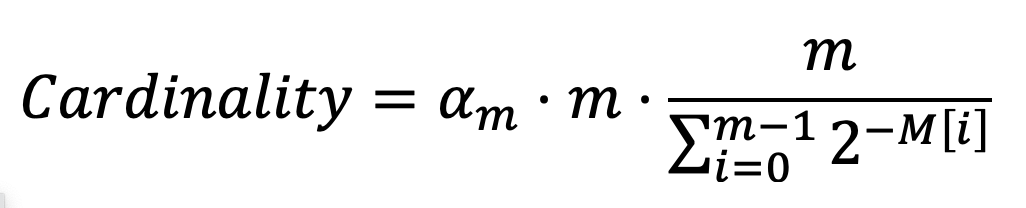
Il s'agit en fait d'une version normalisée de la moyenne harmonique des 2M[i], où αm est une constante calculée par m comme suit :
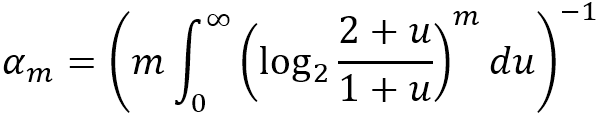
HyperANF
HyperANF est un algorithme ANF populaire, c'est une avancée significative en termes de vitesse et d'évolutivité.
L'algorithme est basé sur l'observation que B(x,t), l'ensemble des nodes atteignables à partir du node x avec une distance t ou moins, satisfait
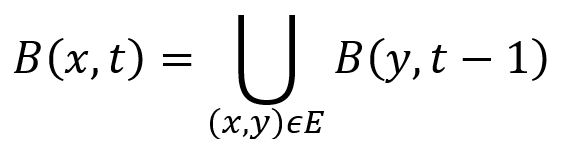
Dans le graph d'exemple ci-dessous, le node a a 3 arêtes adjacentes (a,b), (a,c) et (a,d), donc B(a,3) = B(b,2) ∪ B(c,2) ∪ B(d,2).
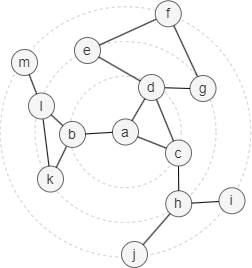
Au lieu de suivre B(x,t), l'algorithme HyperANF utilise des compteurs HyperLogLog pour simplifier le processus de calcul, comme expliqué ci-dessous avec le graph d'exemple ci-dessus :
- Chaque node x est mappé à une représentation binaire h(x), et se voit attribuer un compteur HyperLogLog Cx(t). Réglez b = 2, donc chaque compteur a m = 2b = 4 registres.
- Cx(0) est alors calculé par la valeur de i et ρ. Remarque : nous utilisons 0 au lieu de -∞ pour le calcul, le résultat est identique.
- À la t-ième itération, pour chaque node x, l'union de
B(y,t-1)((x,y)∈E) est réalisée en combinant les compteurs de tous les voisins du node x, c'est-à-dire en maximisant les valeurs du compteur du node x registre par registre. - La valeur de tous les compteurs reste inchangée après 6 itérations, la raison étant que le diamètre du graph est 6.
|B(x,t)|est calculé à chaque itération par l'équation de cardinalité avec la constante αm = 0.53243.
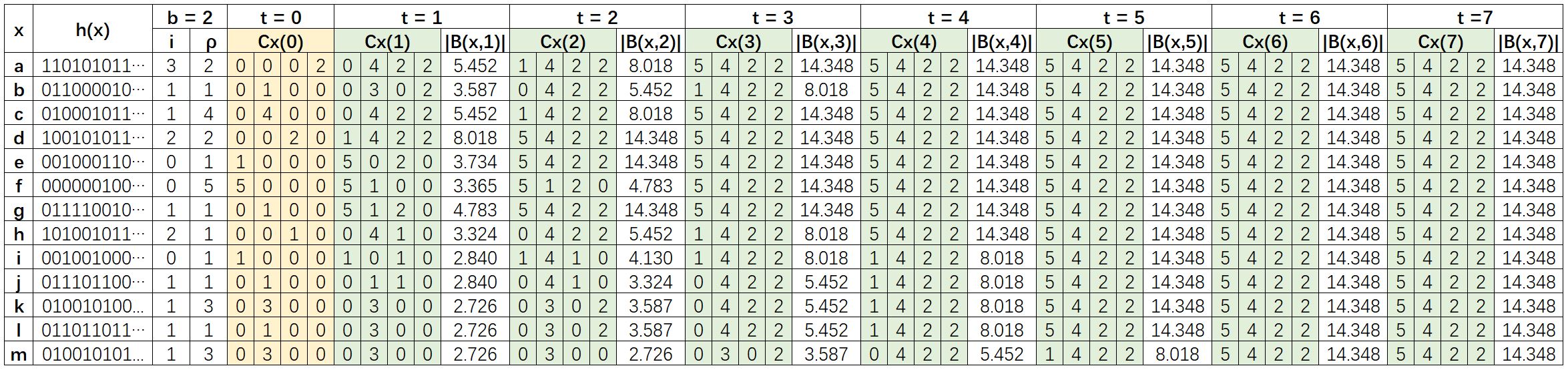
Puisque B(x,0) = {x}, alors |N(x,t)| = |B(x,t)| - 1. Dans cet exemple, la distance moyenne dans un graph calculée par l'algorithme est 3.2041. La distance moyenne exacte du graph dans cet exemple est 3.
Considérations
- L'algorithme HyperANF est généralement mieux adapté aux graphes connectés. Pour les graphes déconnectés, l'algorithme peut ne pas fournir de résultats précis.
- L'algorithme HyperANF ignore la direction des arêtes mais les calcule comme des arêtes non dirigées.
Syntaxe
- Commande :
algo(hyperANF) - Paramètres :
Nom |
Type |
Spec |
Default |
Optionnel |
Description |
|---|---|---|---|---|---|
| loop_num | int | >=1 | / | Non | Le nombre maximal d'itérations |
| register_num | int | [4,30] | / | Non | La valeur de b qui détermine le nombre de registres (m = 2b) dans les compteurs HyperLogLog |
Exemples
Le graph d'exemple est ci-dessous :
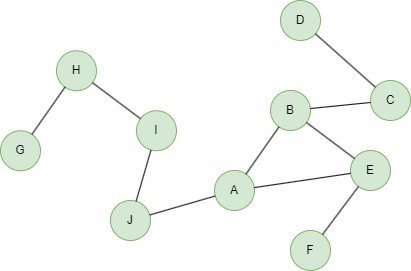
Direct Return
| Alias Ordinal | Type |
Description |
Columns |
|---|---|---|---|
| 0 | KV | La distance moyenne estimée du graph | hyperANF_result |
algo(hyperANF).params({
loop_num: 5,
register_num: 4
}) as distance
return distance
Résultats : distance
| hyperANF_result |
|---|
| 2.50702004427638 |
Stream Return
| Alias Ordinal | Type |
Description |
Columns |
|---|---|---|---|
| 0 | KV | La distance moyenne estimée du graph | hyperANF_result |
algo(hyperANF).params({
loop_num: 7,
register_num: 5
}).stream() as distance
return round(distance.hyperANF_result)
Résultats : 3
Stats Return
| Alias Ordinal | Type |
Description |
Columns |
|---|---|---|---|
| 0 | KV | La distance moyenne estimée du graph | hyperANF_result |
algo(hyperANF).params({
loop_num: 7,
register_num: 10
}).stats() as distance
return distance
Résultats : distance
| hyperANF_result |
|---|
| 2.90383835352478 |

