Vue d’ensemble
La centralité de vecteur propre mesure le pouvoir ou l'influence d'un node. Dans un réseau orienté, le pouvoir d'un node provient de ses voisins entrants. Ainsi, le score de centralité de vecteur propre d'un node dépend non seulement du nombre de liens entrants qu'il a, mais aussi de la puissance de ses voisins entrants. Les connexions avec des nodes à score élevé contribuent davantage au score du node que les connexions avec des nodes à faible score. Dans le scénario de propagation de maladie, un node avec une plus haute centralité de vecteur propre est plus susceptible d'être proche de la source d'infection, ce qui nécessite des précautions particulières.
Le bien connu PageRank est une variante de la centralité de vecteur propre.
La centralité de vecteur propre prend des valeurs entre 0 et 1, les nodes avec des scores plus élevés étant plus influents dans le réseau.
Concepts
Centralité de Vecteur Propre
La puissance (score) de chaque node peut être calculée de manière récursive. Prenez le graph ci-dessous comme exemple, la matrice adjacente A reflète les liens entrants de chaque node. En initialisant que chaque node a un score de 1, et il est représenté par le vecteur s(0).

À chaque tour de transition de puissance, mettez à jour le score de chaque node par la somme des scores de tous ses voisins entrants. Après un tour, le vecteur s(1) = As(0) est comme suit, la normalisation L2 est appliquée pour remettre à l'échelle :

Après k itérations, s(k) = As(k-1) = Aks(0). À mesure que k augmente, s(k) se stabilise. Dans cet exemple, la stabilisation est atteinte après environ 20 tours.
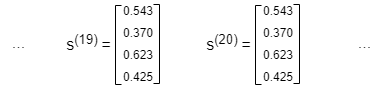
En fait, s(k) converge vers le vecteur propre de la matrice A qui correspond à la plus grande valeur propre absolue, d'où les éléments dans s(k) sont appelés centralité de vecteur propre.
Valeur Propre et Vecteur Propre
Étant donné A est une matrice carrée n x n, λ est une constante, x est un vecteur non-nul n x 1. Si l'équation Ax = λx est vraie, alors λ est appelée la valeur propre de A, et x est le vecteur propre de A qui correspond à la valeur propre λ.
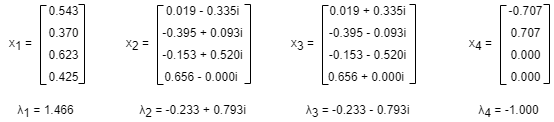
La matrice ci-dessus A a 4 valeurs propres λ1, λ2, λ3 et λ4 qui correspondent respectivement aux vecteurs propres x1, x2, x3 et x4. x1 est le vecteur propre correspondant à la valeur propre dominante λ1 qui a la plus grande valeur absolue.
Selon le théorème de Perron-Forbenius, si la matrice A a des valeurs propres |λ1| > |λ2| ≥ |λ3| ≥ ... ≥ |λn|, alors à mesure que k → ∞, la direction de s(k) = Aks(0) converge vers x1, et s(0) peut être n'importe quel vecteur non nul.
Itération de Puissance
Pour la meilleure efficacité de calcul et précision, cet algorithme adopte l'approche d'itération de puissance pour calculer le vecteur propre dominant (x1) de la matrice A:
- s(1) = As(0)
- s(2) = As(1) = A2s(0)
- ...
- s(k) = As(k-1) = Aks(0)
L'algorithme continue jusqu'à ce que s(k) converge dans certaines tolérances, ou que le nombre maximum d'itérations soit atteint.
Considérations
- L'algorithme utilise la somme de la matrice d'adjacence et de la matrice unité (c'est-à-dire, A = A + I) plutôt que seulement la matrice d'adjacence pour garantir la convergence.
- Le score de centralité de vecteur propre des nodes sans lien entrant converge vers 0.
- La boucle sur soi-même est comptée comme un lien entrant, son poids n'étant compté qu'une seule fois (graph pondéré).
Syntaxe
- Commande :
algo(eigenvector_centrality) - Paramètres :
Nom |
Type |
Spéc |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| max_loop_num | int | ≥1 | 20 |
Oui | Nombre maximum de tours d'itérations ; l'algorithme se termine après avoir fonctionné pour tous les tours, même si la condition de tolerance n'est pas respectée |
| tolerance | float | (0,1) | 0.001 |
Oui | Lorsque tous les scores changent moins que la tolérance entre les itérations, le résultat est considéré comme stable et l'algorithme se termine |
| edge_weight_property | @<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Propriété(s) de l'arête à utiliser comme poids des arêtes, où les valeurs de plusieurs propriétés sont additionnées |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par le score de centralité |
Exemples
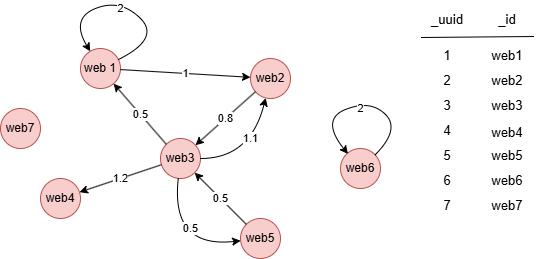
L'exemple est un réseau web, la propriété d'arête @link.value peut être utilisée comme pondération :
File Writeback
| Spéc | Contenu |
|---|---|
| filename | _id,rank |
algo(eigenvector_centrality).params({
max_loop_num: 15,
tolerance: 0.01
}).write({
file: {
filename: 'rank'
}
})
Résultats : Fichier rank
web7,4.63007e-06
web6,0.0198426
web5,0.255212
web3,0.459901
web4,0.255214
web2,0.573512
web1,0.573511
Property Writeback
| Spéc | Contenu | Écrire dans | Type de données |
|---|---|---|---|
| property | rank |
Node property | float |
algo(eigenvector_centrality).params({
edge_weight_property: 'value'
}).write({
db: {
property: 'ec'
}
})
Résultats : Le score de centralité pour chaque node est écrit dans une nouvelle propriété nommée ec
Direct Return
| Ordre Alias | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []parNode | Node et sa centralité | _uuid, rank |
algo(eigenvector_centrality).params({
max_loop_num: 20,
tolerance: 0.01,
edge_weight_property: '@link.value',
order: 'desc'
}) as ec
return ec
Résultats : ec
| _uuid | rank |
|---|---|
| 1 | 0.73133802 |
| 6 | 0.48346400 |
| 2 | 0.43551901 |
| 3 | 0.17412201 |
| 4 | 0.098612003 |
| 5 | 0.041088000 |
| 7 | 0.0000000 |
Stream Return
| Ordre Alias | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []parNode | Node et sa centralité | _uuid, rank |
Exemple : Calculez la centralité de vecteur propre pondérée pour tous les nodes, comptez le nombre de nodes avec un score supérieur à 0,4 ou autrement respectivement
algo(eigenvector_centrality).params({
edge_weight_property: '@link.value'
}).stream() as ec
with case
when ec.rank > 0.4 then 'attention'
when ec.rank <= 0.4 then 'normal'
END as r
group by r
return table(r, count(r))
Résultats : table(r, count(r))
| r | count(r) |
|---|---|
| attention | 3 |
| normal | 4 |

