Vue d’ensemble
La clause k-hop khop().src().depth() récupère les nodes voisins qu'un node peut atteindre en K sauts (à travers K arêtes) les plus courts. Ces voisins sont communément appelés les voisins k-hop du node source.
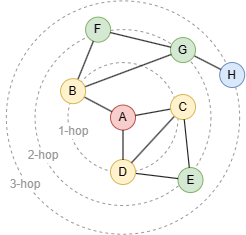
Le voisin k-hop est l'un des concepts fondamentaux de la théorie des graphes. Dans le graphe ci-dessus, les nodes B, C et D sont les voisins à 1 saut du node A, les nodes E, F et G sont les voisins à 2 sauts du node A, et le node H est le voisin à 3 sauts du node A.
La valeur de k est unique et dépend de la longueur des chemins les plus courts entre deux nodes. Par exemple, bien qu'il existe de nombreux chemins entre les nodes A et C (A-C, A-D-C, A-D-E-C), la distance la plus courte est 1. Le node C ne devrait pas apparaître dans les résultats autres que les voisins à 1 saut.
Les résultats des requêtes k-hop sont dédupliqués. Par exemple, il existe deux chemins les plus courts entre les nodes A et E, mais E devrait n'apparaître qu'une seule fois dans la requête à 2 sauts du node A.
La requête k-hop d'Ultipa adopte la technique de parcours BFS pour trouver les chemins les plus courts et les voisins k-hop. Des optimisations ont été appliquées pour améliorer la performance de la requête k-hop. Il est recommandé d'utiliser la requête k-hop au lieu d'autres méthodes de requête de chemin pour cet objectif.
Syntaxe
- Alias de la clause : type NODE
- Méthodes :
Méthode |
Type de Paramètre |
Spécification du Paramètre |
Requis |
Description | Alias |
|---|---|---|---|---|---|
src() |
Filtre | / | Oui | Les conditions pour spécifier le seul node source | NODE |
depth() |
Intervalle | / | Oui | Profondeur pour la recherche (N≥1) :depth(N): N sautsdepth(:N): 1~N sautsdepth(M:N): M~N sauts (M≥0)Quand une plage est définie, la clause retourne les nodes voisins dans l'ordre du plus proche au plus éloigné |
N/A |
node_filter() |
Filtre | / | Non | Les conditions pour spécifier tous les nodes (autres que le node source) dans les chemins de requête | N/A |
edge_filter() |
Filtre | / | Non | Les conditions pour spécifier toutes les arêtes dans les chemins de requête | N/A |
direction() |
Chaîne | gauche, droite |
Non | Direction de toutes les arêtes dans les chemins de requête | N/A |
limit() |
Entier | ≥-1 | Non | Nombre de résultats à retourner pour chaque sous-requête, -1 signifie retourner tous |
N/A |
L'exclusion de certains nodes ou arêtes via
node_filter()ouedge_filter()pourrait induire un changement structurel au graphe, influençant potentiellement les résultats de la requête. Voir les exemples sous Filtrage de Nœud et Filtrage d'Arête.
Exemples
Exemple de Graphe
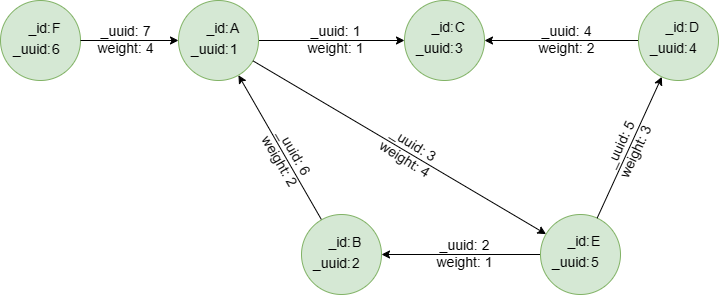
Exécutez ces UQLs ligne par ligne dans un graphset vide pour créer ce graphe :
create().edge_property(@default, "weight", int32)
insert().into(@default).nodes([{_id:"A", _uuid:1}, {_id:"B", _uuid:2}, {_id:"C", _uuid:3}, {_id:"D", _uuid:4}, {_id:"E", _uuid:5}, {_id:"F", _uuid:6}])
insert().into(@default).edges([{_uuid:1, _from_uuid:1, _to_uuid:3, weight:1}, {_uuid:2, _from_uuid:5, _to_uuid:2 , weight:1}, {_uuid:3, _from_uuid:1, _to_uuid:5 , weight:4}, {_uuid:4, _from_uuid:4, _to_uuid:3 , weight:2}, {_uuid:5, _from_uuid:5, _to_uuid:4 , weight:3}, {_uuid:6, _from_uuid:2, _to_uuid:1 , weight:2}, {_uuid:7, _from_uuid:6, _to_uuid:1 , weight:4}])
Définir la Profondeur
Trouver les voisins à 3 sauts du node D.
khop().src({_id == "D"}).depth(3) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| F | 6 |
Trouver les voisins de 1 à 3 sauts du node D.
khop().src({_id == "D"}).depth(:3) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| F | 6 |
| B | 2 |
| A | 1 |
| C | 3 |
| E | 5 |
Retourner le Nœud Source
Trouver les voisins de 1 à 2 sauts du node D. Retourner en même temps le node D.
khop().src({_id == "D"}).depth(0:2) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| B | 2 |
| A | 1 |
| C | 3 |
| E | 5 |
| D | 4 |
Filtrage de Nœud
Trouver les voisins à 3 sauts du node D en excluant le node E.
khop().src({_id == "D"}).depth(3).node_filter({_id != "E"}) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| F | 6 |
| B | 2 |
Lorsque le node E (et ses arêtes adjacentes) est exclu, le node B devient le voisin à 3 sauts du node D.
Filtrage d'Arête
Trouver les voisins à 3 sauts du node D en excluant l'arête 5.
khop().src({_id == "D"}).depth(3).edge_filter({_uuid != 5}) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| E | 5 |
| F | 6 |
| B | 2 |
Lorsque l'arête 5 est exclue, les nodes E et B deviennent les voisins à 3 sauts du node D.
Définir la Direction de l'Arête
Trouver les voisins de 1 à 2 sauts du node D tout en s'assurant que toutes les arêtes traversées pointent vers la droite.
khop().src({_id == "D"}).depth(:2).direction(right) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| C | 3 |
Utiliser l'Alias dans src()
Trouver les voisins à 1 saut des nodes D et F.
find().nodes({_id in ["D", "F"]}) as start
khop().src(start).depth(1).direction(right) as n
return table(start._id, n._id)
Résultat :
| start._id | n._id |
|---|---|
| D | C |
| F | A |
Utiliser limit()
Trouver trois voisins de 1 à 3 sauts du node D.
khop().src({_id == "D"}).depth(:3).limit(3) as n
return n{*}
Résultat :
| _id | _uuid |
|---|---|
| A | 1 |
| C | 3 |
| E | 5 |
La clause k-hop renvoie les nodes voisins dans l'ordre du plus proche au plus éloigné, en commençant par 1-saut, suivi de 2-sauts, puis 3-sauts.
Utiliser OPTIONAL
Trouver les voisins à 2 sauts des nodes A et D tout en s'assurant que toutes les arêtes traversées pointent vers la droite. Retourner null si aucun voisin n'est trouvé.
find().nodes({_id in ["A", "D"]}) as start
optional khop().src(start).depth(2).direction(right) as n
return table(start._id, n._id)
Résultat :
| start._id | n._id |
|---|---|
| A | D |
| A | B |
| D | null |

