Vue d’ensemble
L'algorithme d'Arbre Recouvrant Minimal (MST) calcule l'arbre recouvrant avec la somme minimale des poids des edges pour chaque composant connecté dans un graph.
Le MST a diverses applications, telles que la conception de réseaux, le clustering et les problèmes d'optimisation où la minimisation du coût ou du poids total est importante.
Concepts
Arbre Recouvrant
Un arbre recouvrant est un sous-graph connecté qui inclut tous les nodes d'un graph connecté G= = (V, E) (ou un composant connecté) et qui forme un arbre (c'est-à-dire, sans cercles). Il peut exister plusieurs arbres recouvrants pour un graph, et chaque arbre recouvrant doit avoir (|V| - 1) edges.
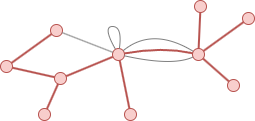
Les 11 nodes dans le graph ci-dessous, avec les 10 edges mis en évidence en rouge, forment un arbre recouvrant de ce graph :
Arbre Recouvrant Minimal (MST)
Le MST est l'arbre recouvrant qui a la somme minimale des poids des edges. La construction du MST commence à partir d'un node de départ donné. Le choix du node de départ n'affecte pas la validité de l'algorithme MST, mais il peut affecter la structure du MST et l'ordre dans lequel les edges sont ajoutés. Différents nodes de départ peuvent aboutir à différents MST, mais tous seront des MST valides pour le graph donné.
Après avoir attribué des poids aux edges dans l'exemple ci-dessus, les trois MST possibles avec différents nodes de départ sont mis en évidence en rouge ci-dessous :
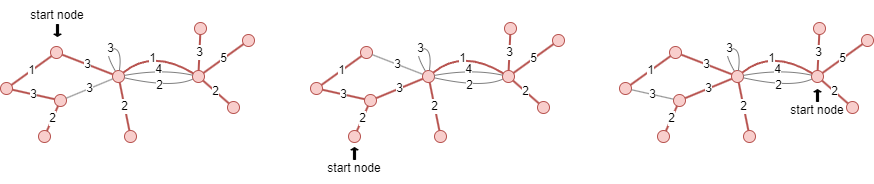
Concernant la sélection des nodes de départ :
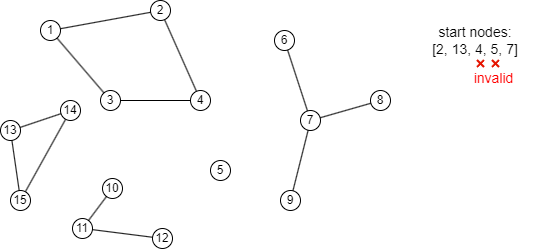
- Chaque composant connecté nécessite seulement un node de départ. Si plusieurs nodes de départ sont spécifiés, le premier sera considéré comme valide.
- Aucun MST ne sera calculé pour les composants connectés qui n'ont pas de node de départ spécifié.
- Les nodes isolés ne sont pas considérés comme des nodes de départ valides pour le calcul du MST.
Considérations
- L'algorithme MST ignore la direction des edges mais les calcule comme des edges non dirigés.
Syntaxe
- Commande :
algo(mst) - Paramètres :
Name |
Type |
Spec |
Default |
Optional |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Yes | ID/UUID des nodes de départ ; le système choisit le node de départ pour chaque composant connecté si non défini |
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | No | Propriétés des edges à utiliser comme poids ; pour chaque edge, la propriété spécifiée avec la plus petite valeur est considérée comme son poids ; les edges sans propriété spécifiée ne seront pas inclus dans aucun MST |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
Exemples
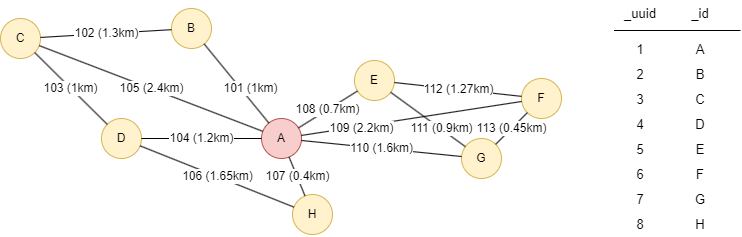
Le graph d'exemple est comme ci-dessous, le node A est un centre électrique, les nodes B~H sont les villages environnants. Chaque edge est étiqueté avec son UUID et la distance entre les emplacements connectés, ce qui représente la longueur de câble requise :
File Writeback
Spec |
Content |
Description |
|---|---|---|
| filename | _id--[_uuid]--_id |
Chemin à un seul pas dans le MST: (node de départ)--(edge)--(node de fin) |
algo(mst).params({
uuids: [1],
edge_schema_property: 'distance'
}).write({
file:{
filename: 'solution'
}
})
Résultats : Fichier solution
A--[107]--H
A--[108]--E
E--[111]--G
F--[113]--G
A--[101]--B
A--[104]--D
C--[103]--D
Direct Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []path | Chemin à un seul pas dans le MST: _uuid (node de départ) -- [_uuid] (edge) -- _uuid (node de fin) |
algo(mst).params({
ids: 'A',
edge_schema_property: '@connect.distance'
}) as mst
return mst
Résultats : mst
| 1--[107]--8 |
| 1--[108]--5 |
| 5--[111]--7 |
| 6--[113]--7 |
| 1--[101]--2 |
| 1--[104]--4 |
| 3--[103]--4 |
Stream Return
Alias Ordinal |
Type |
Description |
|---|---|---|
| 0 | []path | Chemin à un seul pas dans le MST: _uuid (node de départ) -- [_uuid] (edge) -- _uuid (node de fin) |
algo(mst).params({
uuids: [1],
edge_schema_property: 'distance'
}).stream() as mst
with pedges(mst) as mstUUID
find().edges(mstUUID) as edges
return sum(edges.distance)
Résultats : 5.65

