Vue d’ensemble
L'algorithme de Louvain est un algorithme largement reconnu et utilisé pour la détection de communautés dans les graphes. Il porte le nom du lieu d'origine de ses auteurs - Vincent D. Blondel et al. de l'Université catholique de Louvain en Belgique. L'objectif principal de l'algorithme est de maximiser la modularité du graphe, et il a acquis en popularité en raison de sa haute efficacité et de la qualité de ses résultats.
- V.D. Blondel, J. Guillaume, R. Lambiotte, E. Lefebvre, Dépliage rapide des communautés dans les grands réseaux (2008)
- H. Lu, Heuristiques parallèles pour la détection évolutive de communautés (2014)
Concepts
Modularity
Dans de nombreux réseaux, les nodes ont tendance à former naturellement des groupes ou des communautés, caractérisés par des connexions denses à l'intérieur d'une communauté et relativement rares entre les communautés.
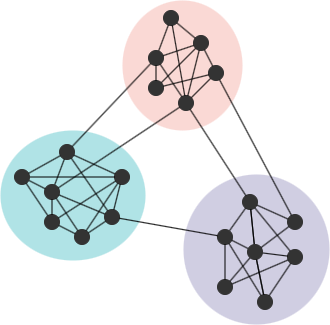
Considérez un réseau équivalent G' à G, où G' conserve la même partition communautaire et le même nombre d'edges que G, mais les edges sont placés aléatoirement. Si G présente une bonne structure communautaire, le ratio d'edges intra-communautaires au nombre total d'edges dans G devrait être plus élevé que le ratio attendu dans G'. Une plus grande disparité entre le ratio réel et la valeur attendue indique une présence plus prononcée d'une structure communautaire dans G. Cela forme le concept originel de modularité. La modularité est l'une des méthodes largement utilisées pour évaluer la qualité d'une partition communautaire, et l'algorithme de Louvain est conçu pour trouver des partitions qui maximisent la modularité.
La modularité varie de -1 à 1. Une valeur proche de 1 indique une structure communautaire plus forte, tandis que des valeurs négatives suggèrent que la partition n'est pas significative. Pour un graphe connecté, la valeur de modularité varie de -0,5 à 1.
En considérant les poids des edges dans le graphe, la modularité (Q) est définie comme suit
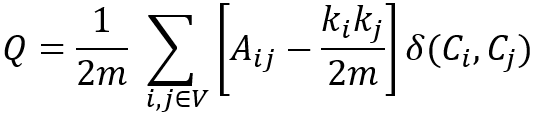
où,
- m est la somme totale des poids des edges dans le graphe ;
- Aij est la somme des poids des edges entre les nodes i et j, et 2m = ∑ijAij ;
- ki est la somme des poids de tous les edges attachés au node i ;
- Ci représente la communauté à laquelle le node i est assigné, δ(Ci,Cj) est 1 si Ci= Cj, et 0 sinon.
Notez que est la somme attendue des poids des edges entre les nodes i et j si les edges sont placés aléatoirement. A la fois Aij et
Nous pouvons également écrire la formule ci-dessus comme suit :
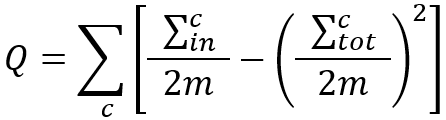
où,
∑ in c ∑ tot c - m a la même signification que ci-dessus, et 2m = ∑c
∑ tot c
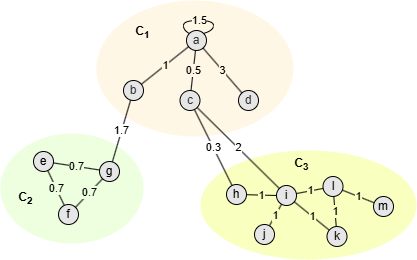
Les nodes dans ce graphe sont assignés à 3 communautés, prenons la communauté C1 en exemple :
∑ in C 1 - (
∑ tot C 1
Louvain
L'algorithme de Louvain commence par une partition singleton, dans laquelle chaque node est dans sa propre communauté. L'algorithme s'exécute ensuite itérativement par passes, et chaque passe est composée de deux phases.
Première Phase : Optimisation de la Modularity
Pour chaque node i, considérez ses voisins j de i, calculez le gain de modularité (ΔQ) qui aurait lieu en réassignant i de sa communauté actuelle à la communauté de j.
Le node i est alors placé dans la communauté qui offre le maximum de ΔQ, mais seulement si ΔQ est supérieur à un seuil positif prédéfini. Si aucun tel gain n'est possible, le node i reste dans sa communauté d'origine.
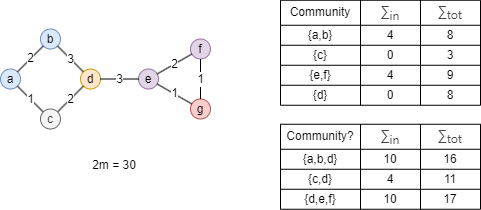
Prenez le graphe ci-dessus comme exemple, les nodes dans la même communauté sont notés de la même couleur. Si vous considérez maintenant le node d, les gains respectifs de modularité de le déplacer vers la communauté {a,b}, {c}, et {e,f} sont :
- ΔQd→{a,b} = Q{a,b,d} - (Q{a,b} + Q{d}) = 52/900
- ΔQd→{c} = Q{c,d} - (Q{c} + Q{d}) = 72/900
- ΔQd→{e,f} = Q{d,e,f} - (Q{e,f} + Q{d}) = 36/900
Si ΔQd→{c} est supérieur au seuil prédéfini de ΔQ, le node d sera déplacé vers la communauté {c}, sinon il restera dans sa communauté d'origine.
Ce processus est appliqué séquentiellement pour tous les nodes et répété jusqu'à ce qu'aucun déplacement individuel ne puisse améliorer la modularité ou que le nombre maximum de boucles soit atteint, complétant ainsi la première phase.
Deuxième Phase : Agrégation de Communautés
Dans la deuxième phase, chaque communauté est agrégée en un node, chaque node agrégé a une self-loop avec un poids correspondant au poids intra-communautaire. Les poids des edges entre ces nouveaux nodes sont donnés par la somme des poids des edges entre nodes dans les deux communautés correspondantes.
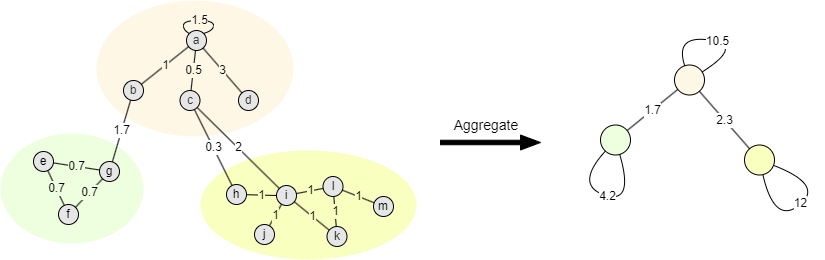
L'agrégation communautaire réduit le nombre de nodes et d'edges dans le graphe sans altérer le poids du graphe local ou entier. Après compression, les nodes à l'intérieur d'une communauté sont traités comme un tout, mais ils ne sont plus isolés pour l'optimisation de la modularité, réalisant un effet de division communautaire hiérarchique (itératif).
Une fois que cette deuxième phase est terminée, une autre passe est appliquée au graphe agrégé. Les passes sont itérées jusqu'à ce qu'il n'y ait plus de changements, et une modularité maximale est atteinte.
Considérations
- Si le node i a une self-loop, lors du calcul de ki, le poids de la self-loop est compté une seule fois.
- L'algorithme de Louvain ignore la direction des edges mais les calcule comme des edges non dirigés.
- La sortie de l'algorithme de Louvain peut varier à chaque exécution, selon l'ordre dans lequel les nodes sont considérés. Cependant, cela n'a pas d'influence significative sur la modularité obtenue.
Syntaxe
- Commande :
algo(louvain) - Paramètres :
Nom |
Type |
Spécification |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| phase1_loop_num | int | ≥1 | 5 |
Oui | Le nombre maximum de boucles de la première phase pendant chaque passe |
| min_modularity_increase | float | [0,1] | 0.01 |
Oui | Le gain minimum de modularité (ΔQ) pour déplacer un node vers une autre communauté |
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Propriétés d'edges à utiliser comme poids, où les valeurs de plusieurs propriétés sont additionnées ; tous les poids d'edges sont considérés comme 1 si non définis |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Triez les communautés par le nombre de nodes qui s'y trouvent (valide seulement en mode 2 de l'exécution stream()) |
Exemples
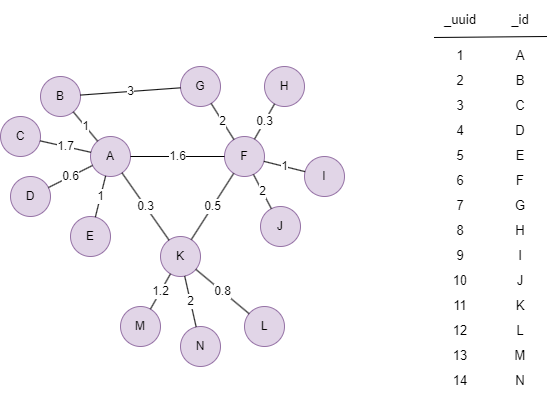
Le graphe d'exemple est le suivant :
File Writeback
| Spécification | Contenu | Description |
|---|---|---|
| filename_community_id | _id,community_id |
Node et son ID de communauté |
| filename_ids | community_id,_id,_id,... |
ID de communauté et l'ID des nodes qu'elle contient |
| filename_num | community_id,count |
ID de communauté et le nombre de nodes qu'elle contient |
algo(louvain).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
file:{
filename_community_id: 'communityID',
filename_ids: 'ids',
filename_num: 'num'
}
})
Statistiques : community_count = 4, modularity = 0.464280
Résultats : Fichiers communityID, ids, num
M,2
N,2
K,2
L,2
J,8
I,8
G,13
H,8
F,8
C,12
E,12
D,12
A,12
B,13
8,J,I,H,F,
12,C,E,D,A,
2,M,N,K,L,
13,G,B,
8,4
12,4
2,4
13,2
Property Writeback
| Spécification | Contenu | Écrire à | Type de données |
|---|---|---|---|
| property | community_id |
Node property | uint32 |
algo(louvain).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
db:{
property: 'communityID'
}
})
Statistiques : community_count = 4, modularity = 0.464280
Résultats : L'ID de communauté de chaque node est écrit dans une nouvelle propriété nommée communityID
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son ID de communauté | _uuid, community_id |
| 1 | KV | Nombre de communautés, modularité | community_count, modularity |
algo(louvain).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}) as results, stats
return results, stats
Résultats : results et stats
| _uuid | community_id |
|---|---|
| 13 | 2 |
| 14 | 2 |
| 11 | 2 |
| 12 | 2 |
| 10 | 8 |
| 9 | 8 |
| 7 | 13 |
| 8 | 8 |
| 6 | 8 |
| 3 | 12 |
| 5 | 12 |
| 4 | 12 |
| 1 | 12 |
| 2 | 13 |
| community_count | modularity |
|---|---|
| 4 | 0.46428 |
Stream Return
| Spécification | Contenu | Alias Ordinal | Type | Description | Colonnes |
|---|---|---|---|---|---|
| mode | 1 ou si non défini |
0 | []perNode | Node et son ID de communauté | _uuid, community_id |
2 |
[]perCommunity | Communauté et le nombre de nodes qu'elle contient | community_id, count |
algo(louvain).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}).stream() as results
group by results.community_id
return table(results.community_id, max(results._uuid))
Résultats : table(results.community_id, max(results._uuid))
| results.community_id | max(results._uuid) |
|---|---|
| 12 | 5 |
| 13 | 7 |
| 2 | 14 |
| 8 | 10 |
algo(louvain).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
order: "desc"
}).stream({
mode: 2
}) as results
return results
Résultats : results
| community_id | count |
|---|---|
| 8 | 4 |
| 12 | 4 |
| 2 | 4 |
| 13 | 2 |
Stats Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Nombre de communautés, modularité | community_count, modularity |
algo(louvain).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1
}).stats() as stats
return stats
Résultats : stats
| community_count | modularity |
|---|---|
| 4 | 0.397778 |
Efficacité de l'algorithme
L'algorithme de Louvain atteint une complexité temporelle plus basse que les algorithmes de détection de communautés précédents grâce à son optimisation gloutonne améliorée, qui est généralement considérée comme O(N*logN), où N est le nombre de nodes dans le graphe, et le résultat est plus intuitif. Par exemple, dans un graphe avec 10 000 nodes, la complexité de l'algorithme de Louvain est d'environ O(40000) ; dans un graphe connecté avec 100 millions de nodes, la complexité de l'algorithme est d'environ O(800000000).
Cependant, en examinant de plus près le processus de l'algorithme, nous pouvons voir que la complexité de l'algorithme de Louvain dépend non seulement du nombre de nodes, mais aussi du nombre d'edges. En gros, on peut l'approcher comme O(N * E/N) = O(E), où E est le nombre d'edges dans le graphe. Cela s'explique par le fait que la logique dominante de l'algorithme de Louvain est de calculer les poids des edges attachés à chaque node.
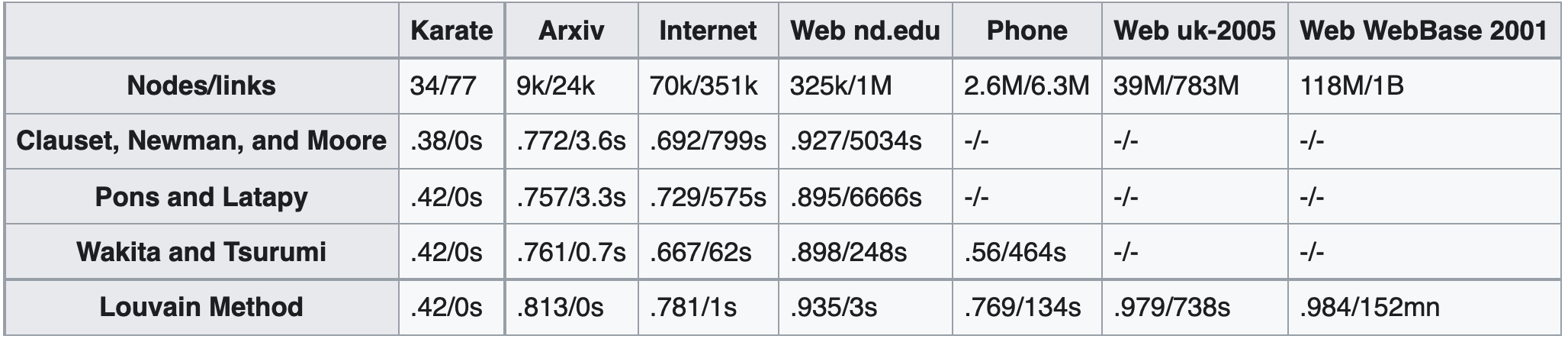
Le tableau ci-dessous montre les performances des algorithmes de détection de communautés de Clauset, Newman et Moore, de Pons et Latapy, de Wakita et Tsurumi, et Louvain, dans des réseaux de diverses tailles. Pour chaque algorithme/réseau, il donne la modularité gagnée et le temps de calcul. Une absence d'entrée indique un temps de calcul supérieur à 24 heures. Cela démontre clairement que Louvain atteint une augmentation significative (exponentielle) à la fois en modularité et en efficacité.
Le choix de l'architecture système et du langage de programmation peut avoir un impact significatif sur l'efficacité et les résultats finaux de l'algorithme de Louvain. Par exemple, une implémentation en série de l'algorithme de Louvain en Python peut entraîner des heures de calcul pour de petits graphes avec environ 10 000 nodes. De plus, la structure de données utilisée peut influencer les performances, car l'algorithme calcule fréquemment les degrés des nodes et les poids des edges.
L'algorithme natif de Louvain adopte le C++, mais il s'agit d'une implémentation en série. La consommation de temps peut être réduite en utilisant autant que possible le calcul parallèle, ce qui améliore ainsi l'efficacité de l'algorithme.
Pour un graphset de taille moyenne avec des dizaines de millions de nodes et d'edges, l'algorithme de Louvain d'Ultipa peut être complété en temps réel. Pour les grands graphes avec plus de 100 millions de nodes et d'edges, il peut être implémenté en quelques secondes à quelques minutes. De plus, l'efficacité de l'algorithme de Louvain peut être affectée par d'autres facteurs, tels que si les données sont écrites dans la propriété de la base de données ou dans un fichier disque. Ces opérations peuvent influencer le temps total de calcul de l'algorithme.

Voici les enregistrements de la modularité et du temps d'exécution de l'algorithme de Louvain s'exécutant sur un graphe avec 5 millions de nodes et 100 millions d'edges. Le processus de calcul prend environ 1 minute, et des opérations supplémentaires, telles que l'écriture dans la base de données ou la génération d'un fichier disque, ajoutent environ 1 minute au temps total d'exécution.

