Vue d’ensemble
L'algorithme de Leiden est un algorithme de détection de communautés conçu pour maximiser la modularité dans un graph. Il a été développé pour résoudre les problèmes potentiels dans les résultats obtenus par l'algorithme Louvain, où certaines communautés peuvent ne pas être bien connectées ou même déconnectées. L'algorithme de Leiden est plus rapide comparé à l'algorithme de Louvain et garantit de produire des partitions dans lesquelles toutes les communautés sont connectées en interne. L'algorithme porte également le nom de l'emplacement de ses auteurs.
- V.A. Traag, L. Waltman, N.J. van Eck, From Louvain to Leiden: guaranteeing well-connected communities (2019)
- V.A. Traag, P. Van Dooren, Y. Nesterov, Narrow scope for resolution-limit-free community detection (2011)
Concepts
Modularity
Le concept de modularité est expliqué dans l'algorithme Louvain. La formule de modularité utilisée dans l'algorithme de Leiden est étendue pour gérer différents niveaux de granularité des communautés :
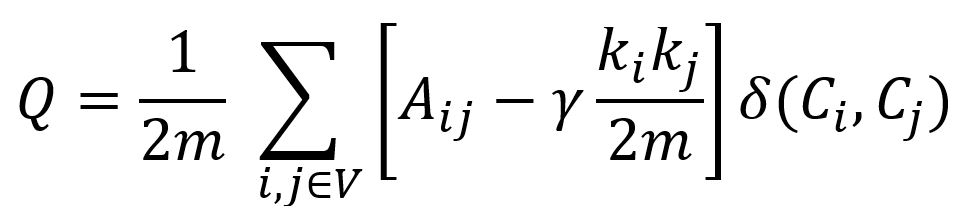
γ > 0 est le paramètre de résolution qui module la densité des connexions au sein des communautés et entre elles. Lorsque γ > 1, cela conduit à des communautés plus nombreuses, plus petites et bien connectées ; lorsque γ < 1, cela conduit à des communautés moins nombreuses, plus grandes et moins bien connectées.
Leiden
L'algorithme de Leiden commence par une partition singleton, dans laquelle chaque node se trouve dans sa propre communauté. Ensuite, l'algorithme parcourt de manière itérative des passes, chaque passe étant composée de trois phases :
Première Phase : Optimisation Rapide de la Modularity
Contrairement à la première phase de l'algorithme de Louvain, qui continue de visiter tous les nodes du graph jusqu'à ce qu'aucun mouvement de node ne puisse augmenter la modularité, l'algorithme de Leiden adopte une approche plus efficace : il visite tous les nodes une seule fois, puis ne visite que les nodes dont le voisinage a changé. Pour ce faire, l'algorithme de Leiden maintient une file d'attente et l'initialise en ajoutant tous les nodes du graph dans un ordre aléatoire.
Ensuite, répétez les étapes suivantes jusqu'à ce que la file d'attente soit vide :
- Retirez le premier node du début de la file d'attente.
- Réassignez le node à une communauté différente qui a le gain maximum de modularité (ΔQ) ; ou gardez le node dans sa communauté d'origine s'il n'y a pas de gain positif.
- Si le node est déplacé vers une communauté différente, ajoutez à l'arrière de la file d'attente tous les voisins du node qui n'appartiennent pas à la nouvelle communauté du node et qui ne sont pas encore dans la file d'attente.
La première phase se termine avec une partition P du graph de base ou agrégé.
Deuxième Phase : Affinement
Cette phase est conçue pour obtenir une partition affinée Prefined de P afin de garantir que toutes les communautés sont bien connectées.
Prefined est initialement définie comme une partition singleton, dans laquelle chaque node dans le graph de base ou agrégé est dans sa propre communauté. Affinez chaque communauté C ∈ P comme suit.
1. Considérez uniquement les nodes v ∈ C qui sont bien connectés au sein de C :
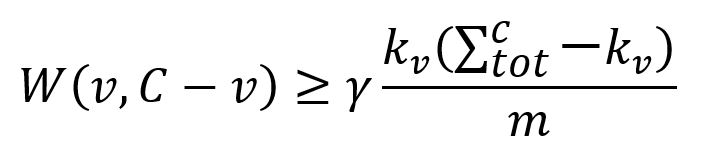
où,
- W(v,C-v) est la somme des poids des edges entre le node v et le reste des nodes de C ;
- kv est la somme des poids de tous les edges attachés au node v ;
- est la somme des poids de tous les edges attachés aux nodes de C.
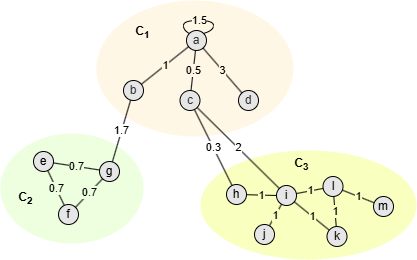
Prenez la communauté C1 dans le graph ci-dessus comme exemple, où
- m = 18,1
- = ka + kb + kc + kd = 6 + 2,7 + 2,8 + 3 = 14,5
Réglez γ à 1,2, puis :
- W(a, C1) - γ/m ⋅ ka ⋅ (
∑ tot C 1 - W(b, C1) - γ/m ⋅ kb ⋅ (
∑ tot C 1 - W(c, C1) - γ/m ⋅ kc ⋅ (
∑ tot C 1 - W(d, C1) - γ/m ⋅ kd ⋅ (
∑ tot C 1
Dans ce cas, seuls les nodes a et d sont considérés comme bien connectés dans la communauté C1.
2. Visitez chaque node v dans un ordre aléatoire, s'il est encore seul dans une communauté de Prefined, fusionnez-le aléatoirement avec une communauté C' ∈ Prefined pour laquelle la modularité augmente. Il est requis que C' soit bien connecté avec C :
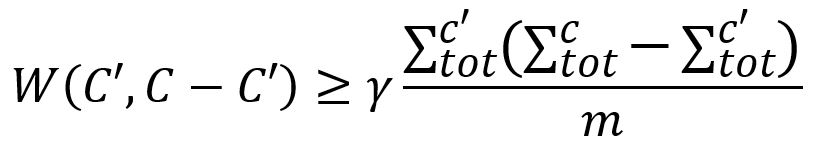
Notez que dans cette phase, chaque node n'est pas nécessairement fusionné de manière gourmande avec la communauté qui offre le gain maximum de modularité. Cependant, plus le gain est grand, plus il est probable qu'une communauté soit sélectionnée. Le degré d'aléatoire dans la sélection d'une communauté est déterminé par un paramètre θ > 0 :
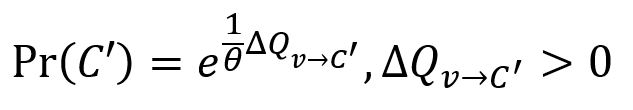
L'aléatoire dans la sélection d'une communauté permet d'explorer plus largement l'espace de partition.
Après la phase d'affinement conclue, les communautés dans P se scindent souvent en plusieurs communautés dans Prefined, mais pas toujours.
Troisième Phase : Agrégation des Communautés
Le graph agrégé est créé sur la base de Prefined. Cependant, la partition pour le graph agrégé est basée sur P. Le processus d'agrégation est le même que celui de Louvain.
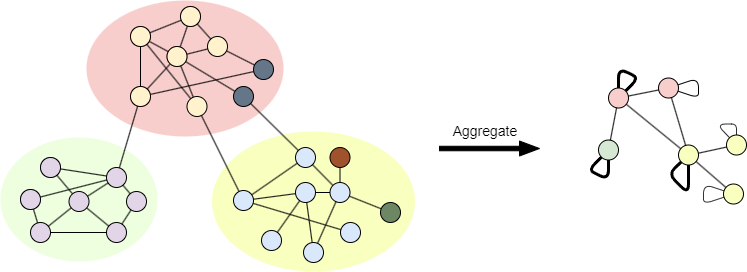
Une fois cette troisième phase terminée, une nouvelle passe est appliquée au graph agrégé. Les passes sont itérées jusqu'à ce qu'il n'y ait plus de changements et qu'une modularité maximale soit atteinte.
Considérations
- Si le node i a une boucle auto, lors du calcul de ki, le poids de la boucle auto est compté une seule fois.
- L'algorithme de Leiden ignore la direction des edges mais les calcule comme des edges non dirigées.
Syntaxe
- Commande :
algo(leiden) - Paramètres :
Nom |
Type |
Specs |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| phase1_loop_num | int | ≥1 | 5 |
Oui | Le nombre maximum de boucles de la première phase pendant chaque passe |
| min_modularity_increase | float | [0,1] | 0.01 |
Oui | Le gain minimum de modularité (ΔQ) pour déplacer un node vers une autre communauté dans la première phase |
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Oui | Les propriétés d'edge à utiliser comme poids, où les valeurs de plusieurs propriétés sont additionnées ; tous les poids d'edge sont considérés comme 1 s'ils ne sont pas définis |
| gamma | float | >0 | 1 | Oui | Le paramètre de résolution γ |
| theta | float | >0 | 0.01 | Oui | Le paramètre θ qui contrôle le degré d'aléatoire lors de la fusion des communautés dans la deuxième phase |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Tri des communautés par le nombre de nodes qu'elles contiennent (uniquement valide dans le mode 2 de l'exécution stream()) |
Exemples
File Writeback
| Specs | Contenu | Description |
|---|---|---|
| filename_community_id | _id,community_id |
Node et son identifiant de communauté |
| filename_ids | community_id,_id,_id,... |
Identifiant de la communauté et l'identifiant des nodes qui y sont inclus |
| filename_num | community_id,count |
Identifiant de la communauté et le nombre de nodes qu'elle contient |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
file:{
filename_community_id: 'communityID',
filename_ids: 'ids',
filename_num: 'num'
}
})
Property Writeback
| Specs | Contenu | Écrire à | Type de Donnée |
|---|---|---|---|
| property | community_id |
Node property | uint32 |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
edge_schema_property: 'weight'
}).write({
db:{
property: 'communityID'
}
})
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son identifiant de communauté | _uuid, community_id |
| 1 | KV | Nombre de communautés, modularité | community_count, modularity |
algo(leiden).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}) as results, stats
return results, stats
Stream Return
| Specs | Contenu | Alias Ordinal | Type | Description | Colonnes |
|---|---|---|---|---|---|
| mode | 1 ou si non défini |
0 | []perNode | Node et son identifiant de communauté | _uuid, community_id |
2 |
[]perCommunity | Communauté et le nombre de nodes qu'elle contient | community_id, count |
algo(leiden).params({
phase1_loop_num: 6,
min_modularity_increase: 0.5,
edge_schema_property: 'weight'
}).stream() as results
group by results.community_id
return table(results.community_id, max(results._uuid))
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1,
order: "desc"
}).stream({
mode: 2
}) as results
return results
Stats Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Nombre de communautés, modularité | community_count, modularity |
algo(leiden).params({
phase1_loop_num: 5,
min_modularity_increase: 0.1
}).stats() as stats
return stats

