Vue d’ensemble
L'algorithme k-Means est un algorithme de classification largement utilisé qui vise à classer les nodes dans un graph en k clusters en fonction de leur similarité. L'algorithme attribue chaque node au cluster dont le centroïde est le plus proche de celui-ci en termes de distance. La distance entre un node et un centroïde peut être calculée à l'aide de différentes métriques de distance, telles que la distance euclidienne ou la similarité cosinus.
Le concept de l'algorithme k-Means remonte à 1957, mais il a été formellement nommé et popularisé par J. MacQueen en 1967 :
- J. MacQueen, Some methods for classification and analysis of multivariate observations (1967)
Depuis lors, l'algorithme a trouvé des applications dans divers domaines, notamment la quantification vectorielle, l'analyse de clustering, l'apprentissage de fonctionnalités, la vision par ordinateur et plus encore. Il est souvent utilisé comme étape de prétraitement pour d'autres algorithmes ou comme méthode autonome pour l'analyse exploratoire des données.
Concepts
Centroïde
Le centroïde ou centre géométrique d'un objet dans un espace N-dimensionnel est la position moyenne de tous les points dans toutes les directions de coordonnées N.
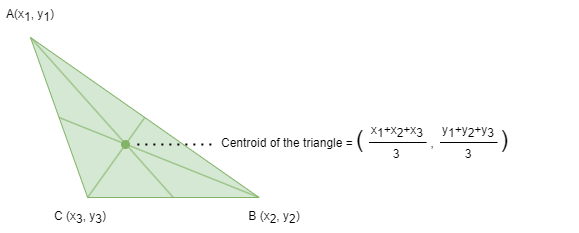
Dans le contexte des algorithmes de clustering comme k-Means, un centroïde désigne le centre géométrique d'un cluster. En spécifiant plusieurs propriétés de node comme caractéristiques de node, le centroïde est le point représentatif qui résume les caractéristiques des nodes au sein du cluster. Pour trouver le centroïde d'un cluster, l'algorithme calcule la valeur moyenne des caractéristiques pour chaque dimension à travers tous les nodes assignés à ce cluster.
L'algorithme débute avec k nodes comme centroïdes initiaux, qui peuvent être spécifiés manuellement ou échantillonnés de manière aléatoire par le système.
Métriques de Distance
L'algorithme k-Means de Ultipa calcule la distance entre un node et un centroïde en utilisant la Distance Euclidienne ou la Similarité Cosinus.
Itérations de Clustering
Pendant chaque processus itératif de k-Means, chaque node dans le graph calcule sa distance à chacun des centroïdes de clusters et est assigné au cluster dont il est le plus proche. Après avoir organisé tous les nodes en clusters, les centroïdes sont mis à jour en recalculant leurs valeurs basées sur les nodes assignés aux clusters respectifs.
L'itération se termine lorsque les résultats de clustering se stabilisent à un certain seuil, ou lorsque le nombre d'itérations atteint la limite.
Considérations
- Le succès de l'algorithme k-Means dépend du choix approprié de la valeur de k et de la sélection de métriques de distance appropriées pour le problème donné. La sélection des centroïdes initiaux affecte également les résultats finaux du clustering.
- S'il existe deux ou plusieurs mêmes centroïdes, un seul d'entre eux prendra effet tandis que les autres centroïdes équivalents formeront des clusters vides.
Syntaxe
- Commande :
algo(k_means) - Paramètres :
Nom |
Type |
Spec |
Par Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| start_ids | []_uuid |
/ | / | Oui | Spécifier des nodes comme les centroïdes initiaux, la longueur du tableau UUID doit être égale à k; ou laisser le système choisir si non défini |
| k | int | [1, |V|] | 1 |
Non | Nombre de clusters souhaités |
| distance_type | int | 1, 2 |
1 |
Oui | Type de la métrique de distance : 1 pour Distance Euclidienne, 2 pour Similarité Cosinus |
| node_schema_property | []@<schema>?.<property> |
Type numérique, doit être ≤ | / | Non | Deux ou plusieurs propriétés de node à utiliser comme caractéristiques de node |
| loop_num | int | ≥1 | / | Non | Le nombre maximum d'itérations |
Exemples
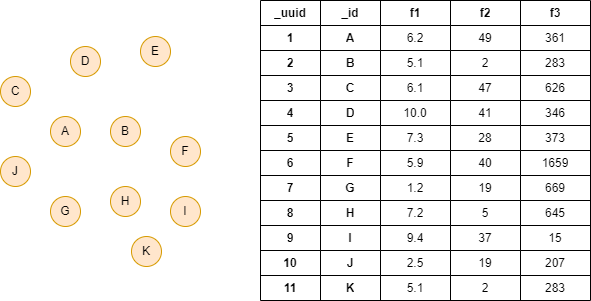
Le graph d'exemple a 11 nodes (les edges sont ignorés), et chaque node a les propriétés f1, f2 et f3 :
File Writeback
Spec |
Contenu |
|---|---|
| filename | community:_id,_id,... |
algo(k_means).params({
start_ids: [1,2,5],
k: 3,
distance_type: 2,
node_schema_property: ['f1', 'f2', 'f3'],
loop_num: 3
}).write({
file:{
filename: 'communities'
}
})
Résultats : Fichier communities
0:I,
1:K,H,G,B,F,
2:J,C,A,E,D,
Direct Return
| Ordinal Alias | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []perCommunity | Cluster et nodes dans le cluster | community, uuids |
algo(k_means).params({
start_ids: [1,2,5],
k: 3,
distance_type: 1,
node_schema_property: ['@default.f1', '@default.f2', '@default.f3'],
loop_num: 3
}) as k3
return k3
Résultats : k3
| community | uuids |
|---|---|
| 0 | 11,5,4,2,1, |
| 1 | 10,9, |
| 2 | 8,7,6,3, |
Stream Return
| Ordinal Alias | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []perCommunity | Cluster et nodes dans le cluster | community, uuids |
algo(k_means).params({
k: 2,
node_schema_property: ['f1', 'f2', 'f3'],
loop_num: 5
}).stream() as c
return c
Résultats : c
| community | uuids |
|---|---|
| 0 | 3,6,8,7, |
| 1 | 5,9,11,10,4,2,1, |

