Vue d’ensemble
L'algorithme de coloration K-1 attribue des couleurs à chaque node de manière à ce que deux nodes adjacents ne partagent pas la même couleur et que le nombre de couleurs utilisées soit minimisé.
Concepts
Coloration
Une coloration d'un graph se réfère souvent à une bonne coloration des nodes, à savoir un étiquetage des nodes du graph avec des couleurs de sorte que deux nodes partageant le même edge n'aient pas la même couleur. La coloration de graph est un problème fondamental en informatique utilisé dans des applications telles que l'ordonnancement, l'allocation de registres et l'attribution de canaux sans fil.
Nombre Chromatique
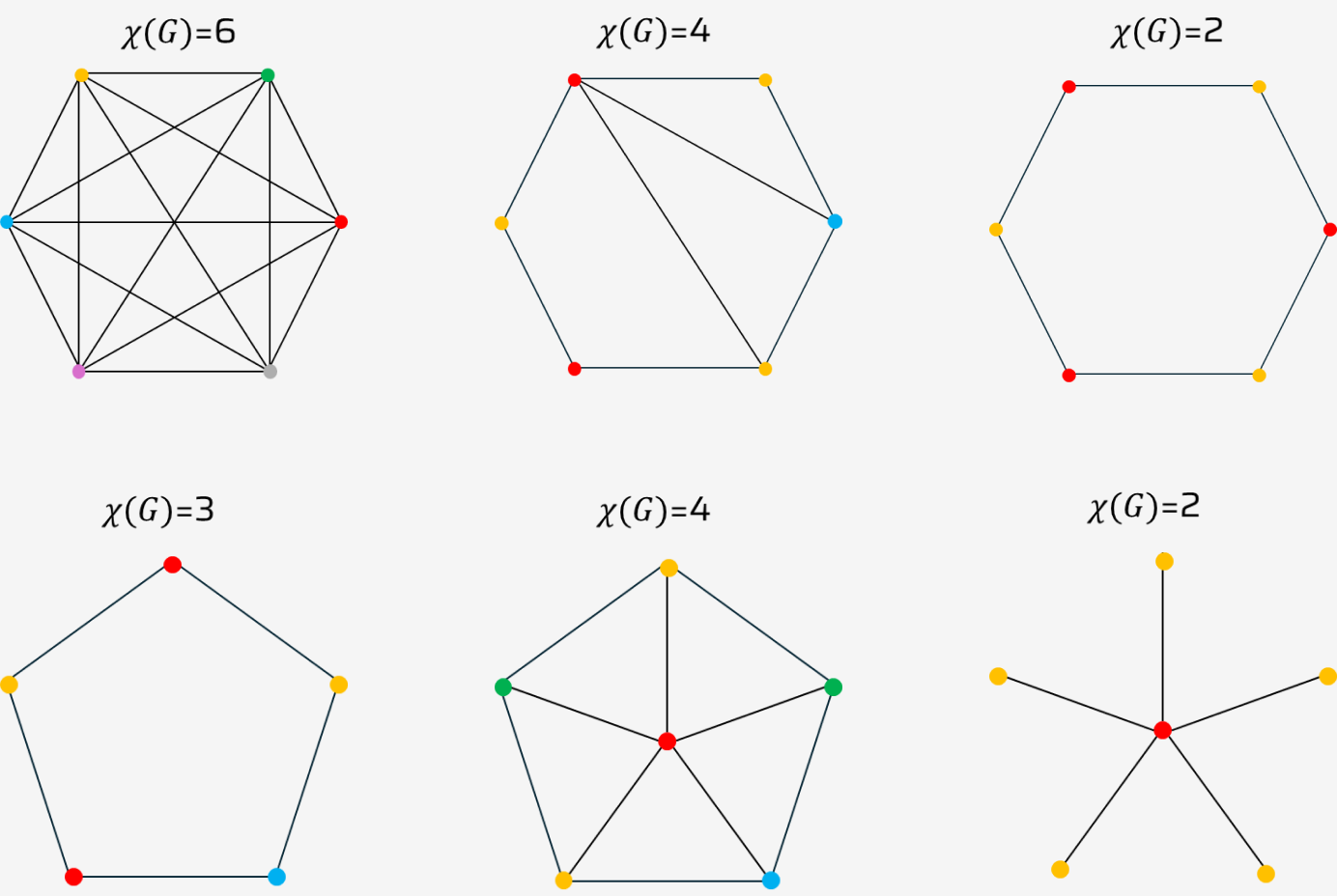
Considérations
La coloration de graph est NP-complète Il est NP-complète de décider si un graph donné admet une k-coloration et NP-difficile de calculer le nombre chromatique. En conséquence, un algorithme glouton est souvent utilisé pour résoudre le problème de coloration de graph pour les graphs de grande taille. En fait, cette approche ne garantit pas la solution optimale et peut colorer les nodes voisins de la même manière. Cependant, augmenter le nombre d'itérations peut améliorer la précision.
Syntaxe
- Commande :
algo(k1_coloring) - Paramètres :
Nom |
Type |
Spéc. |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| loop_num | int | >=1 | 5 |
Oui | Nombre d'itérations |
| version | int | 1, 2 |
2 |
Oui | 1 pour algorithme de coloration gloutonne séquentielle, 2 pour algorithme de coloration gloutonne parallèle itératif |
Exemples
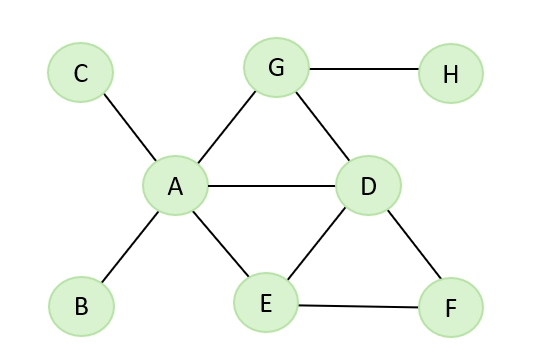
Le graph d'exemple est le suivant :
File Writeback
| Spéc. | Contenu | Description |
|---|---|---|
| filename_community_id | _id,community_id |
Node et son ID de communauté |
| filename_ids | community_id,_id,_id,... |
ID de la communauté et ID des nodes qui s'y trouvent |
| filename_num | community_id,count |
ID de la communauté et le nombre de nodes qui s'y trouvent |
Property Writeback
| Spéc. | Contenu | Écrire vers | Type de Donnée |
|---|---|---|---|
| property | community_id |
Node property | uint32??? 不是string吗 |
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son ID de communauté | _uuid, community_id |
| 1 | KV | Nombre de communautés, modularité | community_count, modularity |
Stream Return
| Spéc. | Contenu | Alias Ordinal | Type | Description | Colonnes |
|---|---|---|---|---|---|
| mode | 1 or if not set |
0 | []perNode | Node et son ID de communauté | _uuid, community_id |
2 |
[]perCommunity | Communauté et le nombre de nodes qu'elle contient | community_id, count |
Stats Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Nombre de communautés | community_count |

