Vue d’ensemble

La centralité harmonique est une variante de la centralité de proximité. La mesure de distance moyenne la plus courte proposée par la centralité harmonique est compatible avec les valeurs infinies qui se produiraient dans un graph déconnecté. La centralité harmonique a été proposée pour la première fois par M. Marchiori et V. Latora en 2000, puis par A. Dekker et Y. Rochat en 2005 et 2009 :

• M. Marchiori, V. Latora, Harmony in the Small-World (2000)
• A. Dekker, Conceptual Distance in Social Network Analysis (2005)
• Y. Rochat, Closeness Centrality Extended to Unconnected Graphs: The Harmonic Centrality Index (2009)

La centralité harmonique prend des valeurs entre 0 et 1, les nodes avec des scores plus élevés ont des distances plus courtes vers tous les autres nodes.

Concepts

Distance la Plus Courte

La distance la plus courte de deux nodes est le nombre de edges contenus dans le chemin le plus court entre eux. Veuillez vous référer à Closeness Centrality pour plus de détails.

Moyenne Harmonique

La moyenne harmonique est l'inverse de la moyenne arithmétique des inverses des variables. La formule pour calculer la moyenne arithmétique A et la moyenne harmonique H est la suivante :

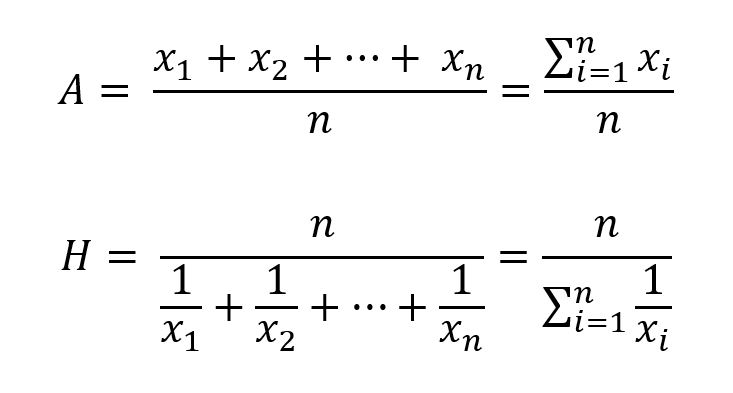
Une application classique de la moyenne harmonique est de calculer la vitesse moyenne lors d'un aller-retour à des vitesses différentes. Supposons qu'il y ait un voyage aller-retour, les vitesses aller et retour sont respectivement de 30 km/h et 10 km/h. Quelle est la vitesse moyenne pour l'ensemble du voyage ?

La moyenne arithmétique A = (30+10)/2 = 20 km/h ne semble pas raisonnable dans ce cas. Comme le voyage de retour prend trois fois plus de temps que l'aller, pendant la majeure partie du voyage, la vitesse reste à 10 km/h, donc nous nous attendons à ce que la vitesse moyenne soit plus proche de 10 km/h.

En supposant qu'une distance aller simple soit de 1, alors la vitesse moyenne qui prend en compte le temps de voyage est 2/(1/30+1/10) = 15 km/h, et c'est la moyenne harmonique, elle est ajustée en fonction du temps passé pendant chaque voyage.

Centralité Harmonique

Le score de centralité harmonique d'un node défini par cet algorithme est l'inverse de la moyenne harmonique des distances les plus courtes du node à tous les autres nodes. La formule est :

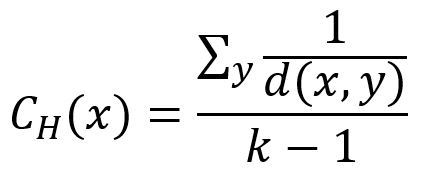
où x est le node cible, y est tout node dans le graph autre que x, k-1 est le nombre de y, d(x,y) est la distance la plus courte entre x et y, d(x,y) = +∞ lorsque x et y ne sont pas accessibles entre eux, dans ce cas 1/d(x,y) = 0.

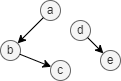
La centralité harmonique du node a dans le graph ci-dessus est (1 + 1/2 + 1/+∞ + 1/+∞) / 4 = 0.375, et la centralité harmonique du node d est (1/+∞ + 1/+∞ + 1/+∞ + 1) / 4 = 0.25.

L'algorithme de Centralité Harmonique consomme des ressources de calcul considérables. Pour un graph avec V nodes, il est recommandé d'effectuer un échantillonnage (uniforme) lorsque V > 10 000, et le nombre d'échantillons suggéré est le logarithme en base 10 du nombre de nodes (log(V)).

Pour chaque exécution de l'algorithme, un échantillonnage est effectué une seule fois, le score de centralité de chaque node est calculé en fonction de la distance la plus courte entre le node et tous les nodes d'échantillonnage.

Considérations

• Le score de centralité harmonique des nodes isolés est 0.

Syntaxe

• Commande : algo(harmonic_centrality)
• Paramètres :

Nom	Type	Spec	Par défaut	Optionnel	Description
ids / uuids	[]_id / []_uuid	/	/	Oui	ID/UUID des nodes à calculer, calcul pour tous les nodes si non défini
direction	string	in, out	/	Oui	Direction de tous les edges dans chaque chemin le plus court, in pour direction entrante, out pour direction sortante
sample_size	int	-1, -2, [1, V]	-1	Oui	Nombre d'échantillons pour calculer les scores de centralité ; -1 signifie échantillonner log(V) nodes ; -2 signifie ne pas effectuer d'échantillonnage ; un nombre dans [1, V] signifie échantillonner le nombre défini de nodes ; sample_size est valide uniquement lorsque ids (uuids) est ignoré ou lorsqu'il spécifie tous les nodes
limit	int	≥-1	-1	Oui	Nombre de résultats à retourner, -1 pour retourner tous les résultats
order	string	asc, desc	/	Oui	Trier les nodes par le score de centralité

Exemples

Le graph d'exemple est le suivant :

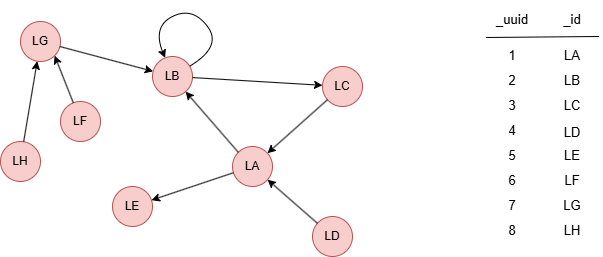
File Writeback

Spec	Contenu
filename	_id,centrality

algo(harmonic_centrality).params().write({
  file:{ 
    filename: 'centrality'
  }
})

Résultats : Fichier centrality

LH,0
LG,0.142857
LF,0.142857
LE,0.357143
LD,0.357143
LC,0.428571
LB,0.428571
LA,0.571429

Property Writeback

Spec	Contenu	Écrire dans	Type de Donnée
property	centrality	Node property	float

algo(harmonic_centrality).params().write({
  db:{ 
    property: 'hc'
  }
})

Résultats : Le score de centralité pour chaque node est écrit dans une nouvelle propriété nommée hc

Direct Return

Alias Ordinal	Type	Description	Colonnes
0	[]perNode	Node et sa centralité	_uuid, centrality

algo(harmonic_centrality).params({
  direction: 'out',
  order: 'desc',
  limit: 3
}) as hc
return hc

Résultats : hc

_uuid	centrality
1	0.35714301
4	0.33333299
3	0.28571400

Stream Return

Alias Ordinal	Type	Description	Colonnes
0	[]perNode	Node et sa centralité	_uuid, centrality

algo(harmonic_centrality).params({
  direction: 'in'
}).stream() as hc
where hc.centrality == 0
return hc

Résultats : hc

_uuid	centrality
8	0.0000000
6	0.0000000
4	0.0000000