Vue d’ensemble
L'algorithme des Composantes Connexes identifie les composantes connexes dans un graph, ce qui est l'indicateur essentiel pour examiner les caractéristiques de connectivité et de topologie du graph.
Le nombre de composantes connexes dans un graph peut servir de méthode de mesure grossière. Si le nombre de composantes connexes reste inchangé après certaines opérations ou modifications du graph, cela suggère que les caractéristiques macroscopiques de connectivité et de topologie du graph n'ont pas été significativement altérées.
Cette information est précieuse dans divers scénarios d'analyse de graph. Par exemple, dans les réseaux sociaux, si le nombre de composantes connexes reste le même au fil du temps, cela implique que les schémas de connectivité globaux et les structures communautaires au sein du réseau n'ont pas subi de changements substantiels.
Concepts
Composante Connexe
Une composante connexe est un sous-ensemble maximal de nodes dans un graph où tous les nodes de ce sous-ensemble sont accessibles les uns aux autres en suivant les edges dans le graph. Un sous-ensemble maximal signifie qu'aucun node supplémentaire ne peut être ajouté au sous-ensemble sans enfreindre l'exigence de connectivité.
Le nombre de composantes connexes dans un graph indique le niveau de déconnexion ou la présence de sous-graphs distincts au sein du graph global. Un graph qui a exactement une composante, consistant en l'ensemble du graph, est appelé un graph connecté.
Composante Faiblement Connexe et Fortement Connexe
Il y a deux concepts importants liés à la composante connexe : composante faiblement connexe (WCC) et composante fortement connexe (SCC):
- Une WCC se réfère à un sous-ensemble de nodes dans un graph dirigé ou non dirigé où il existe un chemin entre n'importe quelle paire de nodes, quelle que soit la direction des edges.
- Une SCC est un sous-ensemble de nodes dans un graph dirigé où il existe un chemin dirigé entre chaque paire de nodes. En d'autres termes, pour n'importe quels deux nodes u et v dans une SCC, il existe un chemin dirigé de u à v et aussi de v à u. Dans le chemin dirigé, tous les edges ont la même direction.
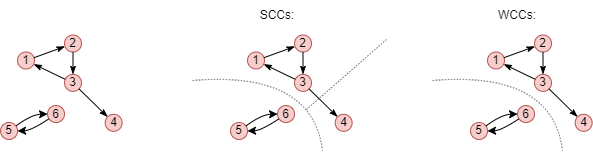
Cet exemple montre les 3 composantes fortement connexes et les 2 composantes faiblement connexes d'un graph. Le nombre de SCC dans un graph est toujours égal ou supérieur au nombre de WCC, car la détermination d'une SCC nécessite des conditions plus strictes par rapport à une WCC.
Considérations
- Chaque node isolé dans le graph est une composante connexe, et c'est à la fois une composante fortement connexe et une composante faiblement connexe.
Syntaxe
- Commande:
algo(connected_component) - Paramètres:
Nom |
Type |
Spec |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| cc_type | int | 1, 2 |
1 |
Oui | 1 signifie composante faiblement connexe (WCC), 2 signifie composante fortement connexe (SCC) |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les résultats par le nombre de nodes dans chaque composante connexe (valide seulement en mode 2 de l'exécution stream()) |
Dans l'algorithme des Composantes Connexes d'Ultipa, chaque composante connexe est désignée comme une communauté.
Exemples
Le graph d'exemple est le suivant:
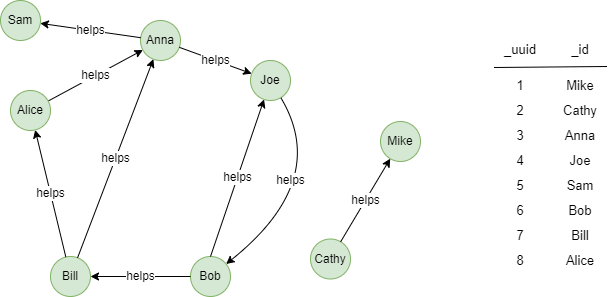
File Writeback
| Spec | Contenu |
|---|---|
| filename_community_id | _id,community_id |
| filename_ids | community_id,_id,_id,... |
| filename_num | community_id,count |
algo(connected_component).params({
cc_type: 1
}).write({
file:{
filename_community_id: 'f1',
filename_ids: 'f2',
filename_num: 'f3'
}
})
Statistiques: community_count = 2
Résultats: Fichiers f1, f2, f3
Alice,0
Bill,0
Bob,0
Sam,0
Joe,0
Anna,0
Cathy,6
Mike,6
0,Alice,Bill,Bob,Sam,Joe,Anna,
6,Cathy,Mike,
0,6
6,2
Property Writeback
| Spec | Contenu | Écrire vers | Type de Données |
|---|---|---|---|
| property | community_id |
Node property | int64 |
algo(connected_component).params().write({
db:{
property: 'wcc_id'
}
})
Statistiques: community_count = 2
Résultats: L'ID de la communauté de chaque node est écrit dans une nouvelle propriété nommée wcc_id
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son ID de communauté | _uuid, community_id |
| 1 | KV | Nombre de communautés | community_count |
algo(connected_component).params({
cc_type: 2
}) as r1, r2
return r1, r2
Résultats: r1 et r2
| _uuid | community_id |
|---|---|
| 8 | 0 |
| 7 | 0 |
| 6 | 0 |
| 5 | 3 |
| 4 | 0 |
| 3 | 0 |
| 2 | 6 |
| 1 | 7 |
| community_count |
|---|
| 4 |
Stream Return
| Spec | Contenu | Alias Ordinal | Type | Description | Colonnes |
|---|---|---|---|---|---|
| mode | 1 ou non défini |
0 | []perNode | Node et son ID de communauté | _uuid, community_id |
2 |
[]perCommunity | Communauté et le nombre de nodes qu'elle contient | community_id, count |
algo(connected_component).params({
cc_type: 2
}).stream() as r
return r
Résultats: r
| _uuid | community_id |
|---|---|
| 8 | 0 |
| 7 | 0 |
| 6 | 0 |
| 5 | 3 |
| 4 | 0 |
| 3 | 0 |
| 2 | 6 |
| 1 | 7 |
algo(connected_component).params({
cc_type: 2,
order: 'asc'
}).stream({
mode: 2
}) as r
return r
Résultats: r
| community_id | count |
|---|---|
| 6 | 1 |
| 7 | 1 |
| 3 | 1 |
| 0 | 5 |
Stats Return
| Alias Ordinal | Type | Description | Colonnes |
|---|---|---|---|
| 0 | KV | Nombre de communautés | community_count |
algo(connected_component).params().stats() as count
return count
Résultats: count
| community_count |
|---|
| 2 |

