Vue d’ensemble
L'algorithme du coefficient de clustering local calcule la densité de connexion parmi les voisins immédiats d'un node. Il quantifie le ratio des connexions réelles entre les voisins par rapport aux connexions maximales possibles.
Le coefficient de clustering local fournit des informations sur la cohésion du réseau égoïste d'un node. Dans le contexte d'un réseau social, le coefficient de clustering local aide à comprendre le degré d'interconnexion entre les amis ou connaissances d'un individu. Un coefficient de clustering local élevé suggère que les amis de la personne sont susceptibles d'être connectés les uns aux autres, indiquant la présence d'un groupe social soudé, tel qu'une famille. À l'inverse, un coefficient de clustering local faible indique un réseau égoïste plus dispersé ou lâchement interconnecté, où les amis de la personne n'ont pas de fortes connexions entre eux.
Concepts
Coefficient de Clustering Local
Mathématiquement, le coefficient de clustering local d'un node dans un graph non orienté est calculé comme le ratio du nombre de paires de voisins connectés par le nombre total de paires de voisins possibles :
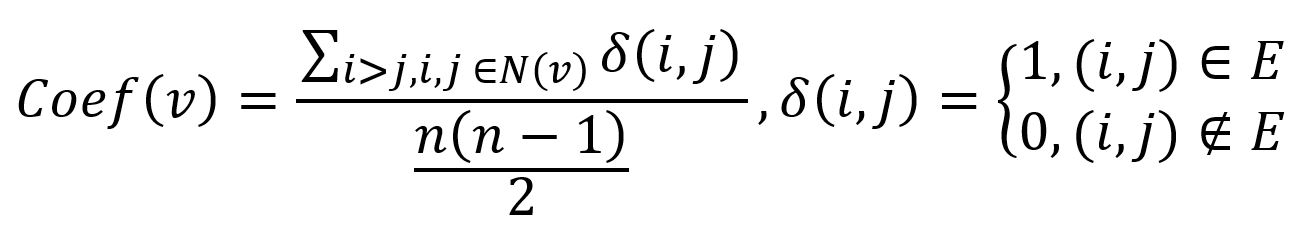
où n est le nombre de nodes contenus dans le voisinage 1-hop du node v (noté N(v)), i et j sont deux node distincts quelconques au sein de N(v), δ(i,j) est égal à 1 si i et j sont connectés, et 0 sinon.
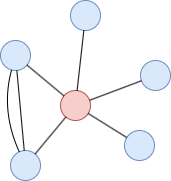
Dans cet exemple, le coefficient de clustering local du node rouge est 1/(5*4/2) = 0.1.
Considérations
- L'algorithme du coefficient de clustering local ignore la direction des edges mais les calcule comme des edges non orientés.
Syntaxe
- Commande :
algo(clustering_coefficient) - Paramètres :
Nom |
Type |
Spec |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Oui | ID/UUID des nodes pour calculer le coefficient de clustering local, calculer pour tous les nodes si non défini |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | string | asc, desc |
/ | Oui | Trier les nodes par la valeur du coefficient de clustering local |
Exemples
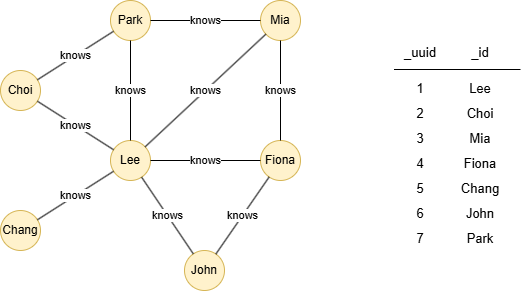
Le graph d'exemple est le suivant :
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id,centrality |
algo(clustering_coefficient).params({
ids: ['Lee', 'Choi']
}).write({
file:{
filename: 'lcc'
}
})
Résultats : Fichier lcc
Lee,0.266667
Choi,1
Property Writeback
| Spec | Contenu | Écrire dans | Type de données |
|---|---|---|---|
| property | centrality |
Node property | float |
algo(clustering_coefficient).params().write({
db:{
property: 'lcc'
}
})
Résultats : La valeur du coefficient de clustering local pour chaque node est écrite dans une nouvelle propriété nommée lcc
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son coefficient de clustering local | _uuid, centrality |
algo(clustering_coefficient).params({
order: 'desc'
}) as lcc
return lcc
Résultats : lcc
| _uuid | centrality |
|---|---|
| 2 | 1 |
| 6 | 1 |
| 3 | 0.666667 |
| 4 | 0.666667 |
| 7 | 0.666667 |
| 1 | 0.266667 |
| 5 | 0 |
Stream Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son coefficient de clustering local | _uuid, centrality |
algo(clustering_coefficient).params().stream() as lcc
where lcc.centrality == 1
return count(lcc)
Résultats : 2

