Vue d’ensemble
La centralité de proximité d’un node est mesurée par la distance moyenne la plus courte du node à tous les autres nodes accessibles. Plus un node est proche de tous les autres nodes, plus il est central. Cet algorithme est largement utilisé dans des applications telles que la découverte de nodes sociaux clés et la recherche des meilleurs emplacements pour des lieux fonctionnels.
L’algorithme de Centralité de Proximité est préférable pour un graph connecté. Pour un graph déconnecté, sa variante, la Centralité Harmonique, est recommandée.
La centralité de proximité prend des valeurs entre 0 et 1, les nodes avec des scores plus élevés ayant des distances plus courtes vers tous les autres nodes.
La centralité de proximité a été définie à l'origine par Alex Bavelas en 1950 :
- A. Bavelas, Communication patterns in task-oriented groups (1950)
Concepts
Distance la Plus Courte
La distance la plus courte entre deux nodes est le nombre d'edges contenu dans le chemin le plus court entre eux. Le chemin le plus court est recherché selon le principe BFS; si le node A est considéré comme le node de départ et le node B est un des voisins K-hop du node A, alors K est la distance la plus courte entre A et B. Veuillez lire K-Hop All pour obtenir des détails sur BFS et les voisins K-hop.
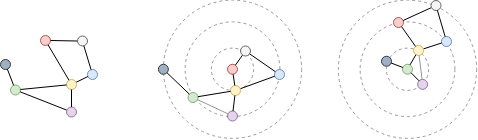
Examinez la distance la plus courte entre les nodes rouge et vert dans le graph ci-dessus. Puisque le graph est non dirigé, peu importe le node de départ (rouge ou vert), l'autre node est le voisin à 2 sauts. Ainsi, la distance la plus courte entre eux est de 2.
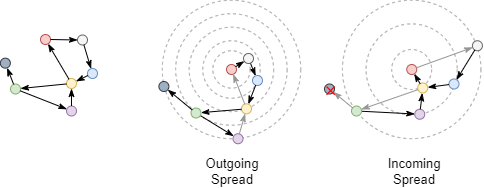
Examinez la distance la plus courte entre les nodes rouge et vert après conversion du graph non dirigé en graph dirigé; la direction des edges doit maintenant être prise en compte. La distance la plus courte sortante du node rouge au node vert est de 4, la distance la plus courte entrante du node vert au node rouge est de 3.
Centralité de Proximité
Le score de centralité de proximité d’un node défini par cet algorithme est l'inverse de la moyenne arithmétique des distances les plus courtes du node à tous les autres nodes accessibles. La formule est :
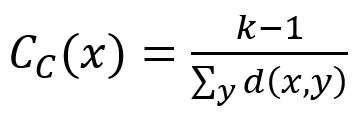
où x est le node cible, y est tout node qui se connecte avec x le long des edges (x lui-même étant exclu), k-1 est le nombre de y, d(x,y) est la distance la plus courte entre x et y.
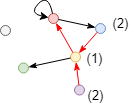
Calculez le score de centralité de proximité du node rouge dans la direction entrante dans le graph ci-dessus. Seuls les trois nodes bleu, jaune et violet peuvent atteindre le node rouge dans cette direction; le score est donc 3 / (2 + 1 + 2) = 0.6. Étant donné que les nodes vert et gris ne peuvent pas atteindre le node rouge dans la direction entrante, ils ne sont pas inclus dans le calcul.
L'algorithme de Centralité de Proximité consomme des ressources de calcul considérables. Pour un graph avec V nodes, il est recommandé de réaliser un échantillonnage (uniforme) lorsque V > 10,000, et le nombre d'échantillons suggéré est le logarithme base-10 du nombre de nodes (
log(V)).
Pour chaque exécution de l'algorithme, l'échantillonnage est effectué une seule fois; le score de centralité de chaque node est calculé en fonction de la distance la plus courte entre le node et tous les nodes échantillons.
Considérations
- Le score de centralité de proximité des nodes isolés est de 0.
- Lors du calcul de la centralité de proximité pour un node, les nodes inaccessibles sont exclus. Par exemple, les nodes isolés, les nodes dans d'autres composants connectés, ou les nodes dans le même composant connecté bien qu'ils ne puissent être atteints dans la direction spécifiée, etc.
Syntaxe
- Commande :
algo(closeness_centrality) - Paramètres :
Nom |
Type |
Spec |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| ids / uuids | []_id / []_uuid |
/ | / | Oui | ID/UUID des nodes à calculer, calculer pour tous les nodes si non défini |
| direction | chaîne | in, out |
/ | Oui | Direction de tous les edges dans chaque chemin le plus court, in pour la direction entrante, out pour la direction sortante |
| sample_size | int | -1, -2, [1, V] |
-1 |
Oui | Nombre d’échantillons pour calculer les scores de centralité ; -1 signifie échantillonner log(V) nodes; -2 signifie ne pas effectuer d’échantillonnage; un nombre compris entre [1, V] signifie échantillonner le nombre fixé de nodes; sample_size est seulement valide quand ids (uuids) est ignoré ou quand il spécifie tous les nodes |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
| order | chaîne | asc, desc |
/ | Oui | Trier les nodes par le score de centralité |
Exemples
Le graph d'exemple est le suivant :
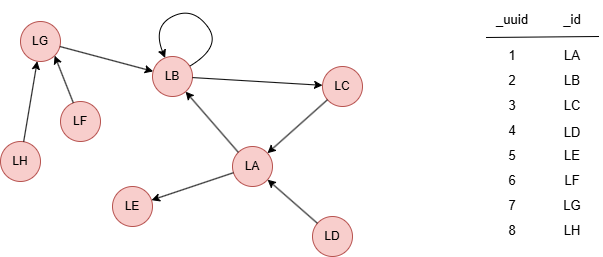
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id,centrality |
algo(closeness_centrality).params().write({
file:{
filename: 'centrality'
}
})
Résultats : Fichier centrality
LA,0.583333
LB,0.636364
LC,0.5
LD,0.388889
LE,0.388889
LF,0.368421
LG,0.538462
LH,0.368421
Property Writeback
| Spec | Contenu | Écrire à | Type de Donnée |
|---|---|---|---|
| property | centrality |
Node property | float |
algo(closeness_centrality).params().write({
db:{
property: 'cc'
}
})
Résultats : Le score de centralité pour chaque node est écrit dans une nouvelle propriété nommée cc
Direct Return
| Alias Ordinal | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et sa centralité | _uuid, centrality |
algo(closeness_centrality).params({
direction: 'out',
order: 'desc',
limit: 3
}) as cc
return cc
Résultats : cc
| _uuid | centrality |
|---|---|
| 1 | 0.75000000 |
| 3 | 0.60000002 |
| 2 | 0.50000000 |
Stream Return
| Alias Ordinal | Type | Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et sa centralité | _uuid, centrality |
algo(closeness_centrality).params({
direction: 'in'
}).stream() as cc
where cc.centrality == 0
return cc
Résultats : cc
| _uuid | centrality |
|---|---|
| 4 | 0.0000000 |
| 6 | 0.0000000 |

