Vue d’ensemble
L'algorithme CELF (Cost Effective Lazy Forward) est utilisé pour sélectionner certains nodes de départ dans un réseau comme source de propagation afin d'atteindre un maximum de nodes. Ceci est connu sous le nom de Maximisation de l'Influence (MI), où 'influence' représente tout ce qui peut être propagé à travers le réseau, tel que la contamination, l'information, la maladie, etc.
CELF a été proposé par Jure Leskovec et al. en 2007, il améliore l'algorithme Greedy traditionnel basé sur le modèle IC en tirant parti de la sous-modularité. Il ne calcule le score de propagation pour tous les nodes qu'au stade initial et ne recalcule pas pour tous les nodes par la suite, donc rentable.
Matériel lié à l'algorithme:
- J. Leskovec, A. Krause, C. Guestrin, C. Faloutsos, J. VanBriesen, N. Glance, Cost-effective Outbreak Detection in Networks (2007)
- D. Kempe, J. Kleinberg, E. Tardos, Maximizing the Spread of Influence through a Social Network (2003)
Une application typique de l'algorithme est de prévenir une épidémie en sélectionnant un petit groupe de personnes à surveiller, afin que toute maladie puisse être détectée à un stade précoce. index-1i9q251ak.js:2 ## Concepts
Fonction de Propagation - Cascade Indépendante
Cet algorithme adopte le modèle Cascade Indépendante (IC) pour simuler le processus de propagation de l'influence dans le réseau. IC est un modèle probabiliste, il commence avec un ensemble de nodes de départ actifs, et à l'étape k:
- Pour chaque node devenu actif à l'étape
k-1, il a une seule chance d'activer chaque voisin sortant inactif avec une probabilité de succès. - Le processus se déroule jusqu'à ce qu'aucune autre activation ne soit possible.
La propagation de l'ensemble de départ donné est mesurée par le nombre de nodes actifs dans le graph à la fin. Ce processus est répété un grand nombre de fois (Simulations de Monte Carlo) et nous le calculons en prenant la moyenne.
Sous-modularité
La fonction de propagation IC() est appelée sous-modulaire car le gain marginal d'un seul node v diminue à mesure que l'ensemble de départ S croît:
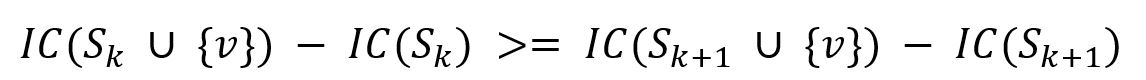
où l'ensemble de départ |Sk+1| > |Sk|, S ∪ {v} signifie ajouter le node v dans l'ensemble de départ.
La sous-modularité de la fonction de propagation est la propriété clé exploitée par CELF. CELF améliore de manière significative l'algorithme Greedy traditionnel utilisé pour résoudre le problème de maximisation de l'influence, il fonctionne beaucoup plus rapidement tout en obtenant des résultats presque optimaux.
Lazy Forward
Lorsque CELF commence, comme Greedy, il calcule la propagation pour chaque node, les met dans une liste triée par propagation décroissante. Comme l'ensemble de départ est vide maintenant, la propagation pour chaque node peut être considérée comme son gain marginal initial.
Dans la première itération, le node en tête de liste est déplacé de la liste à l'ensemble de départ.
Dans l'itération suivante, ne calculez que le gain marginal pour le node actuel en tête. Après le tri, si ce node reste en tête, déplacez-le dans l'ensemble de départ; sinon, répétez le processus pour le nouveau node en tête.
Contrairement à Greedy, CELF évite de calculer le gain marginal pour tous les autres nodes à chaque itération, c'est là que la sous-modularité de la fonction de propagation est prise en compte - le gain marginal de chaque node dans ce tour est toujours inférieur au tour précédent. Donc, si le node en tête reste en tête, nous pouvons le mettre directement dans l'ensemble départ sans calculer pour les autres nodes.
L'algorithme s'arrête lorsque l'ensemble de départ atteint la taille de l'ensemble. index-1i9q251ak.js:2 ## Syntaxe
- Commande :
algo(celf) - Paramètres :
Nom |
Type |
Spécification |
Par défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| seedSetSize | int | >0 | 1 |
Oui | La taille de l'ensemble de départ |
| monteCarloSimulations | int | >0 | 1000 |
Oui | Le nombre de simulations de Monte Carlo |
| propagationProbability | float | (0,1) | 0.1 |
Oui | La probabilité que chaque voisin sortant soit activé avec succès par un node ayant la capacité d'activation dans certains tours |
| index-1i9q251ak.js:2 ## Exemples |
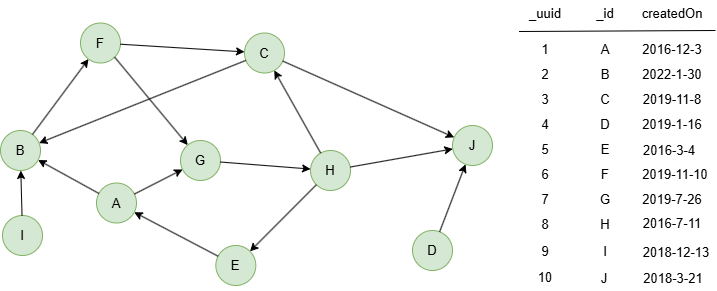
Le graph d'exemple est le suivant :
File Writeback
| Spécification | Contenu | Description |
|---|---|---|
| filename | _id,spread |
Node et son gain marginal lorsqu'il rejoint l'ensemble de départ |
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.5
}).write({
file:{
filename: 'seeds'
}
})
Résultats: Fichier seeds
I,4.687
D,1.261
X,1
Direct Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son gain marginal lorsqu'il rejoint l'ensemble de départ | _uuid, spread |
algo(celf).params({
seedSetSize: 2,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}) as seeds
return seeds
Résultats: seeds
| _uuid | spread |
|---|---|
| 9 | 5.345 |
| 4 | 1.262 |
Stream Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node et son gain marginal lorsqu'il rejoint l'ensemble de départ | _uuid, spread |
algo(celf).params({
seedSetSize: 3,
monteCarloSimulations: 1000,
propagationProbability: 0.6
}).stream() as seeds
find().nodes({_uuid == seeds._uuid}) as nodes
return table(nodes._id, nodes.createdOn, seeds.spread)
Résultats: table(nodes._id, nodes.createdOn, seeds.spread)
| nodes._id | nodes.createdOn | seeds.spread |
|---|---|---|
| I | 2018-12-13 00:00:00 | 5.345 |
| D | 2019-01-16 00:00:00 | 1.262 |
| X | 2022-06-13 00:00:00 | 1 |

