Vue d’ensemble
L’algorithme bipartite est utilisé pour déterminer si un graph donné est un graph bipartite. En appliquant l’algorithme, il devient possible d'identifier et d'exploiter la structure inhérente des graph bipartites dans différents scénarios, permettant ainsi une allocation efficace des ressources, l’attribution des tâches et l’optimisation du regroupement.
Concepts
Graph Bipartite
Un graph bipartite, également connu sous le nom de bigraph, est un graph dont les node peuvent être divisés en deux ensembles disjoints, de sorte que chaque edge du graph connecte un node d'un ensemble à un node de l'autre ensemble. En d'autres termes, il n'y a pas d'edges qui connectent des node au sein du même ensemble.

Ce graph d'exemple est bipartite. Les node peuvent être partitionnés en ensembles V1 = {A, D, E} et V2 = {B, C, F}.
Méthode de Coloration
Pour déterminer si un graph est bipartite, une approche courante consiste à effectuer un parcours du graph et à attribuer chaque node visité à l'un des deux ensembles différents. Ce processus est souvent appelé "coloration" des node. Lors du parcours, si un edge est rencontré qui connecte deux node au sein du même ensemble, alors le graph n'est pas bipartite. À l'inverse, si tous les edges connectent les node de différents ensembles, le graph est bipartite.
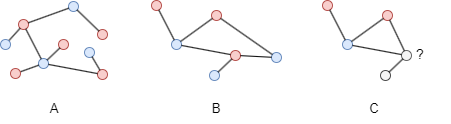
Dans cet exemple, à la fois le graph A et le graph B sont bipartites. Le graph C n'est pas bipartite car il contient un cycle impair. Un cycle impair est un cycle qui a un nombre impair de node. Les graph bipartites ne peuvent pas contenir de cycles impairs car il n'est pas possible de colorer tous les node d'un cycle impair en utilisant seulement deux couleurs tout en respectant l'exigence de bipartition. Cette propriété, selon laquelle les graph bipartites ne contiennent jamais de cycles impairs, est une caractéristique fondamentale des graph bipartites.
Considérations
- Les deux extrémités d'une boucle auto-référentielle sont le même node ; ainsi, les graph qui ont une telle boucle ne sont pas bipartites.
- L’algorithme bipartite ignore la direction des edges mais les considère comme des edges non orientés.
Syntaxe
- Commande :
algo(bipartite) - Cet algorithme n’a pas de paramètres.
Exemples
Le graph d'exemple est le suivant :
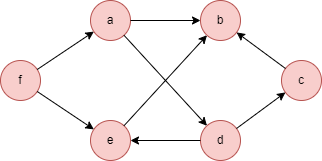
Direct Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Si le graph est bipartite, 0 signifie faux, 1 signifie vrai | bipartite_result |
algo(bipartite).params() as result
return result
Résultats : result
| bipartite_result |
|---|
| 1 |
Stream Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Si le graph est bipartite, 0 signifie faux, 1 signifie vrai | bipartite_result |
algo(bipartite).params().stream() as result
return result
Résultats : result
| bipartite_result |
|---|
| 1 |
Stats Return
Alias Ordinal |
Type |
Description | Colonnes |
|---|---|---|---|
| 0 | KV | Si le graph est bipartite, 0 signifie faux, 1 signifie vrai | bipartite_result |
algo(bipartite).params().stats() as result
return result
Résultats : result
| bipartite_result |
|---|
| 1 |

