Vue d’ensemble
LINE (Large-scale Information Network Embedding) est un modèle d'incorporation de réseau qui préserve les structures de réseau locales ou globales. LINE est capable de s'adapter à des réseaux de très grande taille de type arbitraire, il a été initialement proposé en 2015 :
- J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, Q. Zhu, LINE: Large-scale Information Network Embedding (2015)
Concepts
Première proximité et Deuxième proximité
Première proximité dans un réseau montre la proximité locale entre deux nodes, et cela dépend de la connectivité. L'existence d'un lien ou d'un lien avec un poids plus grand (poids négatif non considéré ici) signifie une plus grande première proximité entre deux nodes ; s'il n'existe aucun lien entre les deux, leur première proximité est de 0.
D'autre part, la deuxième proximité entre une paire de nodes est la similitude entre leurs structures voisines, qui est déterminée par les voisins partagés. Au cas où deux nodes n'ont pas de voisins communs, leur deuxième proximité est de 0.
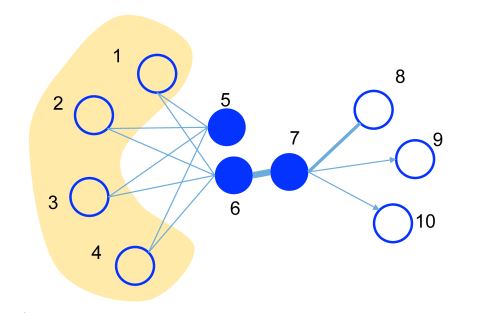
Ceci est un exemple illustratif, où l'épaisseur de l'edge signifie son poids.
- Un poids substantiel sur l'edge entre les nodes 6 et 7 indique une première proximité élevée. Ils doivent avoir des représentations proches dans l'espace d'incorporation.
- Bien que les nodes 5 et 6 ne soient pas directement connectés, leurs voisins communs considérables établissent une deuxième proximité notable. Ils sont également censés être représentés de manière proche les uns aux autres dans l'espace d'incorporation.
Modèle LINE
Le modèle LINE est conçu pour intégrer des nodes dans le graph G = (V,E) en vecteurs de faible dimension, préservant la première ou la deuxième proximité entre les nodes.
LINE avec première proximité
Pour capturer la première proximité, LINE définit la probabilité conjointe pour chaque edge (i,j)∈E reliant les nodes vi et vj comme suit :
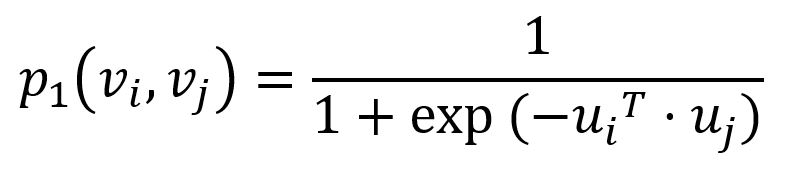
ou ui est la représentation vectorielle de faible dimension du node vi. La probabilité conjointe p1 varie de 0 à 1, avec deux vecteurs plus proches résultant en un produit scalaire plus élevé et, par conséquent, une probabilité conjointe plus élevée.
Empiriquement, la probabilité conjointe entre le node vi et vj peut être définie comme
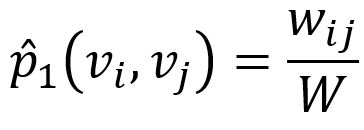
où wij désigne le poids de l'edge entre les nodes vi et vj, W est la somme de tous les poids d'edges dans le graph.
La divergence KL est adoptée pour mesurer la différence entre deux distributions :
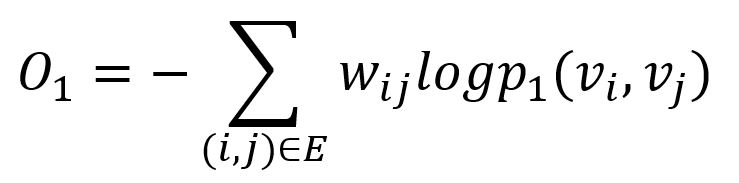
Cela sert de fonction objective qui doit être minimisée lors de l'entraînement, en préservant la première proximité.
LINE avec deuxième proximité
Pour modéliser la deuxième proximité, LINE définit deux rôles pour chaque node - l'un comme le node lui-même, l'autre comme "contexte" pour les autres nodes (ce concept provient du modèle Skip-gram). En conséquence, deux représentations vectorielles sont introduites pour chaque node.
Pour chaque edge (i,j)∈E, LINE définit la probabilité que le "contexte" vj soit observé par le node vi comme
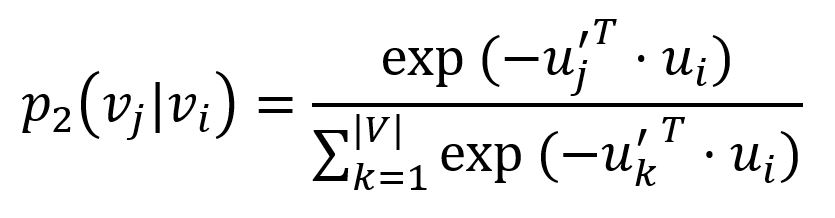
ou u'j est la représentation du node vj quand il est considéré comme le "contexte". Il est important de noter que le dénominateur implique le totalité du "contexte" dans le graph.
La probabilité empirique correspondante peut être définie comme
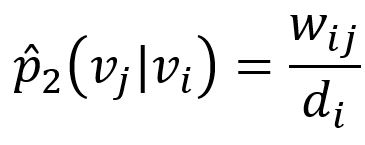
ou wij est le poids de l'edge (i,j), di est le degré pondéré du node vi.
De même, la divergence KL est adoptée pour mesurer la différence entre deux distributions :
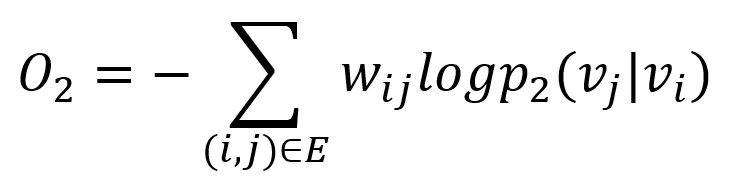
Cela sert de fonction objective qui doit être minimisée lors de l'entraînement, en préservant la deuxième proximité.
Optimisation du Modèle
Échantillonnage Négatif
Pour améliorer l'efficacité du calcul, LINE adopte l'approche d'échantillonnage négatif qui échantillonne plusieurs edges négatifs selon une certaine distribution de bruit pour chaque edge (i,j). Plus précisément, les deux fonctions objectives sont ajustées comme :
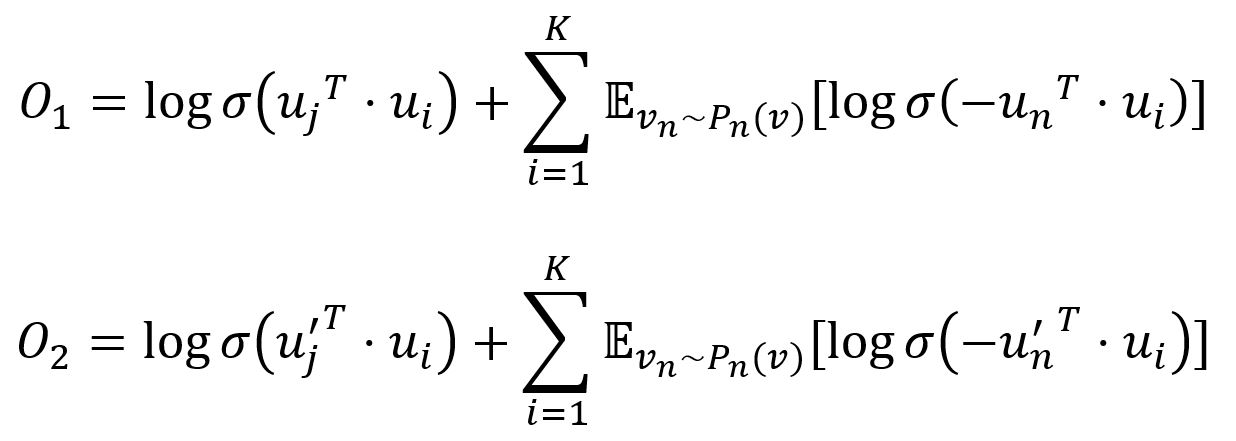
ou σ est la fonction sigmoid, K est le nombre d'edges négatifs tirés de la distribution de bruit Pn(v) ∝ dv3/4, dv est le degré pondéré du node v.
Échantillonnage d'Edges
Étant donné que les poids des edges sont inclus dans les deux objectifs, ces poids seront multipliés dans les gradients, entraînant l'explosion des gradients et compromettant ainsi la performance. Pour y remédier, LINE échantillonne les edges avec des probabilités proportionnelles à leurs poids, et traite ensuite les edges échantillonnés comme des edges binaires pour la mise à jour du modèle.
Considérations
- L'algorithme LINE ignore la direction des edges mais les calcule comme des edges non dirigées.
Syntaxe
- Commande:
algo(line) - Paramètres :
Nom |
Type |
Spec |
Défaut |
Optionnel |
Description |
|---|---|---|---|---|---|
| edge_schema_property | []@<schema>?.<property> |
Type numérique, doit être LTE | / | Non | Propriété(s) des edges à utiliser comme poids d'edge(s), où les valeurs de plusieurs propriétés sont additionnées |
| dimension | int | ≥2 | / | Non | Dimensionnalité des incorporations |
| train_total_num | int | ≥1 | / | Non | Nombre total d'itérations d'entraînement |
| train_order | int | 1, 2 |
1 |
Oui | Type de proximité à préserver, 1 signifie première proximité, 2 signifie deuxième proximité |
| learning_rate | float | (0,1) | / | Non | Taux d'apprentissage utilisé initialement pour entraîner le modèle, qui diminue après chaque itération d'entraînement jusqu'à atteindre min_learning_rate |
| min_learning_rate | float | (0,learning_rate) |
/ | Non | Seuil minimum pour le taux d'apprentissage alors qu'il est progressivement réduit pendant l'entraînement |
| neg_num | int | ≥0 | / | Non | Nombre d'échantillons négatifs à produire pour chaque échantillon positif, il est suggéré de définir entre 0 et 10 |
| resolution | int | ≥1 | 1 |
Oui | Paramètre utilisé pour améliorer l'efficacité de l'échantillonnage négatif ; une valeur plus élevée offre une meilleure approximation à la distribution de bruit d'origine ; il est suggéré de définir comme 10, 100, etc. |
| limit | int | ≥-1 | -1 |
Oui | Nombre de résultats à retourner, -1 pour retourner tous les résultats |
Exemple
File Writeback
| Spec | Contenu |
|---|---|
| filename | _id,embedding_result |
algo(line).params({
dimension: 20,
train_total_num: 10,
train_order: 1,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 5,
resolution: 100,
limit: 100
}).write({
file:{
filename: 'embeddings'
}})
Property Writeback
| Spec | Contenu | Écrire dans | Type de Donnée |
|---|---|---|---|
| property | embedding_result |
Node Property | string |
algo(line).params({
edge_schema_property: '@branch.distance',
dimension: 20,
train_total_num: 10,
train_order: 1,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 5,
limit: 100
}).write({
db:{
property: 'vector'
}})
Direct Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node and its embeddings | _uuid, embedding_result |
algo(line).params({
edge_schema_property: '@branch.distance',
dimension: 20,
train_total_num: 10,
train_order: 1,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 5,
limit: 100
}) as embeddings
return embeddings
Stream Return
| Alias Ordinal | Type |
Description |
Colonnes |
|---|---|---|---|
| 0 | []perNode | Node and its embeddings | _uuid, embedding_result |
algo(line).params({
edge_schema_property: '@branch.distance',
dimension: 20,
train_total_num: 10,
train_order: 2,
learning_rate: 0.01,
min_learning_rate: 0.0001,
neg_number: 5,
limit: 100
}).stream() as embeddings
return embeddings

